🔄 最終更新日 2020年7月13日 by takara_semi
本記事では中学数学1年で学習するすべての項目について、その概要を確認します。それではさっそく、中1で学んだ数学の内容を見ていきましょう。中1 > 1章:正負の数
本章では小さい数から大きい数を引く計算を学び「数の世界」を広げます。
正負の数
様々な「高い」「低い」と「正の数(正の符号$+$のついた数)」と「負の数(負の符号$-$のついた数)」を理解しましょう。例えば富士山の標高は $+3776$m 青函トンネルの最深部の標高は $-240$m です。埼玉の熊谷市では $+41℃$ 北海道の旭川市では $-41℃$ を記録しています。色々な数に触れて正負の数に慣れましょう。
正の数:$0$ より大きい数
例
$+7$, $+1.5$, +$\frac{1}{3}$
例
$-3$, $-0.7$, $-\frac{5}{2}$
例
$1,2,3,…$
$a$ の絶対値:数直線上で原点から点 $a$ までの距離のこと。
例
$-3$ の絶対値は $3$, $+3$ の絶対値も $3$ となる。負の数は絶対値が大きいほど数の大小としては小さい数になる。
加法と減法
本節では正負の数の加法(足し算)と減法(引き算)について学びます。例えば $(+5)+(-3)$ と $5-3$ は等しいでしょうか。計算結果は同じですが、正負の数の考え方を理解するためには、これらの式の違いを理解する必要があります。計算や数の意味を数直線などを利用して正しく理解しましょう。
加法①:同符号の2数の和:加法の結果を「和」という。同符号の2数の和では絶対値の和に共通の符号をつける。
例
$(-3)+(-2)$$=-(3+2)$$=-5$
(1) 絶対値の差に絶対値が大きい方の符号をつける。
例
$(+3)+(-2)$$=+(3-2)$$=-1$
例
$(+97)+(-97)=0$
例
$(-8)+0=-8$, $0+(+3)=3$
例
$(+8)-(-2)$$=(+8)+(+2)$$=10$ つまり $-2$ を引くことは $+2$ を加えることと同じ。
※ $0$ との減法:どんな数から $0$ を引いても差ははじめの数になる。
例
$(-3)-0=-3$, $0-(+10)=10$
(1) 左から順に計算する。
(2) 加法と減法の混じった式では加法だけの式にする。
例
$(+3)+(-5)-(-6)-(+2)$$=(+3)+(-5)+(+6)+(-2)$
※ $+3, -5, -6, +2$ を式の項という。
例
$(+3)+(-5)+(+6)+(-2)$$=(3+6)+(-5-2)$$=(+9)+(-7)=2$
乗法と除法
正負の数の乗法(掛け算)の考え方を理解しましょう。特に、負の数を掛けることが、数直線上で反対方向へ向かうイメージを持ち、2数の積・商(乗法・除法の結果)の符号を間違えないようにしましょう。
同符号の2数の積・商:絶対値の積・商に $+$ の符号をつける。
例
$(-1) \times (-1)=1$
例
$(-1) \times (+1)=-1$
例
$376 \times 0=0$, $0 \div 33=0$, $3 \div 0$ は計算できない。
数学が面白くなる動画―1
0で割ると数学の世界がめちゃくちゃになる?「0で割る」を禁止する理由。
数学が面白くなる動画―2
無限大にも大きさはあるのでしょうか?かんがえてみましょう。
例1)$3 \times 3 = 3^2$($3$ の $2$ 乗。指数は$2$。$2$乗を平方ともいう)
例2)$3 \times 3 \times 3= 3^3$($3$ の $3$乗。指数は$3$。$3$乗を立方ともいう)
逆数:2つの数の積が $1$ のとき一方の数を他方の数の逆数という。
(1) $-3$ の逆数は $(-3) \times \left(-\frac{1}{3} \right)=1$ であるから $-\frac{1}{3}$ だと分かる。
(2) 逆数を利用することで除法を乗法になおすことができる。
例
$10 \div (-5)$$=10 \times \left(-\frac{1}{5} \right)$$=-2$
※ 分数の負の数の表現について:
(2) $\frac{a}{-b}$$=a \div (-b)$$=-(a \div b)$$=-\frac{a}{b}$ である。
(1)(2)より、分数の分子もしくは分母に $-$ が付いているときは分数の前に移動させることができる。
乗法と除法の混じった式:除法は逆数を利用して乗法に直して計算する。また符号は負の数が奇数個あれば $-$ 負の数が偶数個あれば $+$ となる。
例
$(-3) \div \frac{1}{3} \times (-2)$$=+(3 \times 3 \times 2)=18$
色々な計算
これまでに学んだ加法・減法・乗法・除法をまとめて四則といいます。本項では四則の色々な計算について考えていきます。2つの正負の数の加法(および減法)や乗法(および除法)では、計算の順番を入れ変えてもその結果は変わりません。これを交換法則といいます。他にも、計算の順序を括弧を用いて変えても計算結果が変わらない結合法則や、式を分けて計算する分配法則などがあります。これらを利用して、一見複雑な計算を工夫して簡単に計算してみましょう。
計算法則:
(1)加法について:
交換法則:$A+B=B+A$
結合法則:$(A+B)+C=A+(B+C)$
分配法則:$(A+B) \times C$$=A \times C+B \times C$
交換法則:$A \times B=B \times A$
結合法則:$(A \times B) \times C=A \times (B \times C)$
分配法則:$A \times (B+C)$$=A \times B+A \times C$
四則の混じった式の計算:
(1) 加減と乗除の混じった計算では乗法・除法を先に計算する。
(2) 括弧のある式の計算では括弧の中を先に計算する。
(3) 累乗のある式の計算では累乗を先に計算する(累乗は乗法としてみることができる)。
例
$-3^2-2 \times (-3)$$=-(3 \times 3)+(-2) \times (-3)$$=-9+6=-3$
例1
身長:平均身長との差を考える。13歳の平均身長が $158$cm だとすると $160$cmのAくんは平均 $+2$cm $155$cmのBくんは平均 $-3$cmと表現できる。
例2
気温:天気予報では前日の気温と比較した今日の気温が書かれていることが多い。前日が $20℃$ で翌日の気温が $17℃$ だった場合は $17℃(-3℃)$ のように書かれる。もし今日の気温が $25℃$ だった場合は $25℃(+5℃)$ のように書かれる。
数学が面白くなる動画―3
なぜ私たちは $=$ や $+$ や $-$ の記号を使うのでしょうか?
数学が面白くなる動画―4
正しい計算の順番で竜を倒す物語。
中1 > 2章:文字と式
小学校では「数」を用いた式を考えてきましたが、本章では「文字」を用いた式を学び、数式の表現の手段を大きく広げましょう。文字式の理解は中学数学理解の根幹となる重要な内容です。「数」と「文字」の違いを正しく理解し、文字を利用した式の表現方法や計算方法について習得しましょう。
文字を使った式
文字を使った式を利用することで、求めたい数を簡単に計算できることが多くあります。例えばマッチ棒を使って正方形を作る時、1個なら $4$ 本 2個なら $7$ 本…となりますが、1000個の正方形を作るにはいくつのマッチ棒が必要でしょうか。実は正方形の数を文字 $x$ と表現すると、必要なマッチ棒の本数は $1+3 \times x$ 本となります。つまり、1000個の正方形を作るには $1+3 \times 1000$$=3001$ 本のマッチ棒が必要であることが分かります。子のように,実際に数えたらきりがない問題も、法則を見つけて文字式で表現することで、簡単に計算することができます。例を挙げればきりがありませんが、中学数学を学び終えた時には、数式に「文字」を利用することがいかに便利なことかを理解できることでしょう。
文字式の表し方:
(1) 乗法の記号 $\times$ をはぶいて書く。
例
$a \times b = ab$
(2) 数を文字の前に書く。
例
$x \times 3 \times y = 3xy$
(3) 同じ文字の積は累乗の指数を使って書く。
例
$a \times b \times b = ab^2$
(4) 除法の記号 $\div$ を使わず分数の形で書く。
例
$3 \times x \div 4 = \frac{3x}{4}$
※ 例えば$\frac{3x}{4}$は$\frac{3}{4}x$,$\frac{a}{5}$は$\frac{1}{5}a$ と書いてもよい。
(5) 文字はアルファベット順に書く。
例
$b \times c \times a = abc$
数量を式で表す:
(1) 代金 $=$ 1個の値段 $\times$ 個数
(2) 道のり $=$ 速さ $\times$ 時間
例
$a$ km の道のりを歩くのに $3$ 時間かかった。歩く速さを求める $\to$ 毎時 $\frac{a}{3}$ km (※距離と速さと時間の関係は正確に理解しておくこと。例えば車などの速さがkm/時のように表されていることを知っていれば、速さ $=\frac{距離(km)}{時間(時)}$ということが分かるので計算を確かめることができる。)
(3) 3けたの整数:$100a+10b+c$
(4) 利益 $=$ 売価 $-$ 原価 $=$ 原価 $\times$ 利益率
(5) 食塩水の濃度(%) $=$ $\frac{食塩の重さ}{食塩水の重さ}\times 100$
(6) 平均 $=$ $\frac{全体の和}{全体の個数}$
(7) 割合:$a$割 $\to$ $\frac{a}{10}$
(8) 割合:$a$% $\to$ $\frac{a}{100}$
例
全校生徒 $b$ 人の学校のうち $31$% の生徒が自転車通学をしている。自転車通学の人数を求める $\to$ $b \times \frac{31}{100}$$=\frac{31}{100}b$ 人
代入と式の値:
式の中の文字を数に置き換えることを代入といい代入して計算した結果を式の値という。
例
$x=-2$ のとき $x^3$ の値を求める。$x^3$ に $x=-2$ を代入すると $(-2)^3$$=(-2) \times (-2) \times (-2) $$=-8$ よって求める式の値は $-8$
文字式の計算
ここでは文字式を計算する方法を学びます。例えば $3+2x$ という式を考えると加法の記号 $+$ で結ばれた $3,2x$ のそれぞれを項といい $2x$ という項で数の部分の $3$ を $x$ の係数といいますまた $2x$ のように文字が1つだけ掛けられている項を1次の項といい、1次の項と数の項の和で表現できる式を1次式といいます。文字式の計算、例えば1次式の計算では、文字の部分が同じ項(同類項)をあつめて計算します。1次式の計算は後に学ぶ1次方程式や関数、2次方程式の計算などの基礎となります。沢山手を動かして文字式の計算に慣れておくと、これから学ぶ多くの数学の内容について得意になることでしょう。
1次式と数との積:1次式の各項にそれぞれ数をかける。分配法則を利用。
例
$3(5x-3)$$=3 \times 5x-3 \times 3$$=15x-9$
1次式の加法・減法:「1次の項」「数の項」どうしでそれぞれ計算する。
例
$(3x-1)-(2x+1)$$=(3x-2x)+(-1-1)$$=x-2$ ※引くことは符号を変えて加えることと同じ。1次式の減法は引く方の式の各項の符号をそれぞれ変えて加える。
等式と不等式:等号 $=$ を使って数量の間の関係を表した式を等式という。また不等号 $ > , < $ を使って数量の間の関係を表した式を不等式という(等号を含む不等式 $≧, ≦$ もある)。等号や不等号の左の部分を左辺、右の部分を右辺、あわせて両辺という。
例1
$a$ は $b$ より大きい $\to$ $a > b$
例2
$a$ は $b$ 以上 $\to$ $a ≧ b$
例3
$a$ は $b$ 以下 $\to$ $a ≦ b$
例4
$a$ は $b$ より小さい(未満) $\to$ $a < b$
※ 数学で使う文字について:数学で使う文字の多くは英単語の頭文字である(例外もある)。英語を知っていると何故この文字を使うのか納得できることが多くある。
(単位1) 速さの単位 $km/h$ の $h$ $\to$ hour(時間)
(単位2) 速さの単位 $m/min$ の $min$ $\to$ minute(分)
(文字1) 「円の半径」の文字 $r$ $\to$ radius(半径)
(文字2) 「長さ」の文字 $\ell$ $\to$ length(長さ)
(文字3) 円周率 $\pi$ $\to$ 円周率 $=$$\frac{円周}{直径}$ で $3.141592…$ と無限に続く数。
数学が面白くなる動画―5
円周率 $\pi$ の歴史と活用方法について考えてみましょう。
中1 > 3章:1次方程式
この章では身近な場面で求めたい数量がある時に、その数量を文字で表現して等式をつくり、その解を求める方法について考えます。問題文から自力で問題に合う1次方程式を考えるには慣れが必要です。たくさんの問題に触れて、自信を持って1次方程式をつくることができるようになりましょう。
1次方程式
式の中の文字に代入する値によって成り立つ場合とそうでない場合がある等式を方程式と言います。たとえば $x+100=200$ という等式は $x=100$ では成り立ちますが $x=200$ では成り立ちません。また方程式を成り立たせる文字の値を方程式の解といいます。先の例では $x=100$ が方程式の解となります。そしてこのように方程式の解を求めることを方程式を解くといいます。また式を移項などで整理することで(1次式)$=0$ $(ax+b=0)$ ただし $a \neq 0$ の形に変形できる方程式を特に1次方程式という。1次方程式の計算では、方程式を解いた後に検算のために式の中の文字に解を代入して成り立つかどうかを確かめるようにしましょう。
等式の性質: $A=B$ ならば:
(1) $A+C=B+C$:両辺に同じ数を足しても等式が成り立つ。
例
\begin{eqnarray}
x-3 &=& 4 \\
x-3+3&=& 4+3 \\
x &=& 7
\end{eqnarray}
(2) $A-C=B-C$:両辺から同じ数を引いても等式が成り立つ。
例
\begin{eqnarray}
x+4 &=& 6 \\
x+4-4&=& 6-4 \\
x &=& 2
\end{eqnarray}
(3) $AC=BC$:両辺に同じ数を掛けても等式が成り立つ。
例
\begin{eqnarray}
\frac{x}{4} &=& 3 \\
\frac{x}{4} \times 4 &=& 3 \times 4 \\
x &=& 12
\end{eqnarray}
(4) $\frac{A}{C}=\frac{B}{C} (C \neq 0)$:両辺を $0$ でない同じ数で割っても等式が成り立つ。
例
\begin{eqnarray}
4x &=& 12 \\
\frac{4x}{4} &=& \frac{12}{4} \\
x &=& 3
\end{eqnarray}
(5) $B=A$:左辺と右辺を入れかえても等式が成り立つ。
例
\begin{eqnarray}
4 &=&2x+8 \\
2x+8&=&4
\end{eqnarray}
1次方程式の解き方:次の手順で解く。
(1) 文字を含む項を左辺に数の項を右辺に移項する。
※ 移項:等式の一方にある項を、その項の符号を変えて他方に移すこと。
(2) 両辺を計算して $ax=b$ の形にする。
(3) $x$ の係数 $a$ で両辺を割って解 $x=\frac{b}{a}$ を求める。
例
\begin{eqnarray}
3x+5 &=& x+9 \\
3x-x &=& 9-5 \\
2x &=& 4 \\
x &=&\frac{4}{2} \\
x &=& 2
\end{eqnarray}
※「$=$」を縦にそろえて書くと分かりやすいため、このような書き方に慣れておくと、とてもよい。方程式の変形は数学の基礎となるため、綺麗に分かりやすく解答することも非常に重要である。
いろいろな形の1次方程式の解き方
(1) かっこを含む1次方程式 $\to$ かっこをはずしてから解く。
例
\begin{eqnarray}
4(-x+4) &=& 3(2x-\frac{4}{3}) \\
-4x+16 &=& 6x-4 \\
-4x-6x &=& -4-16 \\
-10x &=& -20\\
x &=& \frac{-20}{-10}\\
x &=& 2
\end{eqnarray}
※ このようにかっこをはずして整数係数の1次方程式として解く。
(2) 小数を含む1次方程式 $\to$ 係数を整数にするために両辺に $10, 100, 1000$ 等をかける。
例
\begin{eqnarray}
0.12x-0.04 &=& 0.1x+0.24 \\1.64
12x-4 &=& 10x+24 \\
12x-10x &=& 24+4 \\
2x &=& 28\\
x &=& \frac{28}{2}\\
x &=& 14
\end{eqnarray}
※ 両辺に $100$ を掛けて整数係数の1次方程式として解く。
(3) 分数を含む1次方程式 $\to$ 分母の最小公倍数を両辺にかける。
例
\begin{eqnarray}
\frac{x-2}{3} &=& \frac{2x}{9}+1\\
\frac{x-2}{3} \times 9 &=& \left( \frac{2x}{9}+1 \right) \times 9\\
3(x-2) &=& 2x+9 \\
3x-6 &=& 2x+9 \\
3x-2x &=& 9+6 \\
x &=& 15
\end{eqnarray}
※ 両辺に分母の最小公倍数である $9$ を掛けて整数係数の1次方程式として解く。また係数に分数を含む方程式で分母の公倍数を両辺にかけて、分数を含まない形に変形することを分母をはらうという。
比例式:比が等しいことを表す式を比例式という。$a:b=c:d$ のとき $ad=bc$ が成り立つ。
例
\begin{eqnarray}
3:4 &=& 2x:5\\
2x \times 4 &=& 3 \times 5\\
8x &=& 15 \\
x &=& \frac{15}{8}
\end{eqnarray}
1次方程式の利用
方程式を利用して様々な問題を解決してみましょう。たくさんの問題に取り組むことで方程式を利用することがいかに便利かを実感することができます。
1次方程式を利用した問題の解法:次の手順で解く:
STEP1:問題の意味を考えて文字を選ぶ(求める数量を $x$ で表す。最初に何を $x$ とするかを明記する)。
STEP2:数量の間の関係を見つけて方程式をつくる。
STEP3:つくった方程式を解く。
STEP4:方程式の解が問題に適するかを確かめる(解の検討)。方程式の解であってもその問題に適しないことがある。
例
STEP1:リンゴとミカンの個数が合わせて10個ある。リンゴの個数を $x$ 個とするとミカンの個数は $10-x$ 個。
STEP2:リンゴが1個200円ミカンが1個50円で合計の代金が1100円だとすると $200x+50(10-x)=1000$ という方程式をつくることができる。
STEP3:
\begin{eqnarray}
200x+50(10-x) &=& 1100 \\
150x &=& 600 \\
x &=& 4
\end{eqnarray}
STEP4:リンゴが4個ミカンが6個のとき確かに合計1100円になるため解として適している。
中1 > 4章:比例と反比例
たとえば1000枚を超える紙束の枚数を数えようと思うと大変です。そこで、枚数を直接数える代わりに紙1枚の重さを調べてから、紙束の重さを量れば、比例の関係から紙束の枚数を求めることができます。このように求めたい数量と関係のある数量をみつけて、その関係を利用することがとても便利な場合があります。本章では、このような便利な比例・反比例の関係を調べたり利用したりする方法を学びましょう。
比例
比例の関係を利用すれば、お店のレジの待ち時間や、家のお風呂のお湯がいっぱいになるまでの時間、出かける時に目的地に着く時間などを予測できるようになります。未来を予測できるようになるのです。ともなって変わる2つの数量の間に成り立つ関係について考え理解を深め、比例の関係の利用方法を習得しましょう。
変数:いろいろな値をとる文字。主に $x$, $y$, $z$ が変数として利用される。
関数:2つの変数 $x$, $y$ があり変数 $x$ の値を決めるとそれにともなって変数 $y$ の値が定まる時 $y$ は $x$ の関数であるという。
変域:変数の取り得る値の範囲。
例
変数 $x$ の取り得る値の範囲が $0$ 以上$5$ 未満のとき $x$ の変域は不等号を使って $0≦x<5$ と表すことができる。
※ 変域を数直線上で表現する場合:端の数を含む場合は ● 含まない場合は ○ を使って表すことが多い。つまり端の数を含む $≧, ≦$ の記号の場合は ● 端の数を含まない $>, <$ の記号の場合は ○ を使って表す。
比例を表す式:$y$ は $x$ に比例 $\to$ $y=ax$ ($a$ は定数で $a \neq 0$) また比例の式の中の文字 $a$ は定数であり比例定数という。
例
縦が $5$cm 横が $x$cm の長方形の面積を $y$${\rm cm^2}$とする。このとき $y$ を $x$ の式で表すと $y=5x$ となる。このとき比例定数は $5$ となる。
座標・比例のグラフ
本節では比例の式 $y=ax$ をグラフとして表現する方法を学びます。グラフの上での点の位置を $x$ と $y$ の値の組 $(x,y)$ で表す方法を理解することは、関数を図を用いて理解するための基礎知識となります。演習を繰り返してグラフでの表現方法と読み取り方法を正しく理解しましょう。
座標:横の直線を $x$ 軸または横軸、縦の直線を $y$ 軸または縦軸、 $x$ 軸 $y$ 軸を合わせて座標軸、座標軸の交点 $O$ を原点という。原点は平面においては $(x,y)=(0,0)$ である。また任意の点 ${\rm P}$ の位置を表すためには ${\rm P}(m,n)$ と書く。このとき $m$ を点 ${\rm P}$ の $x$ 座標 $n$ を点 ${\rm P}$ の $y$ 座標 $(m,n)$ を点 ${\rm P}$ の座標という。
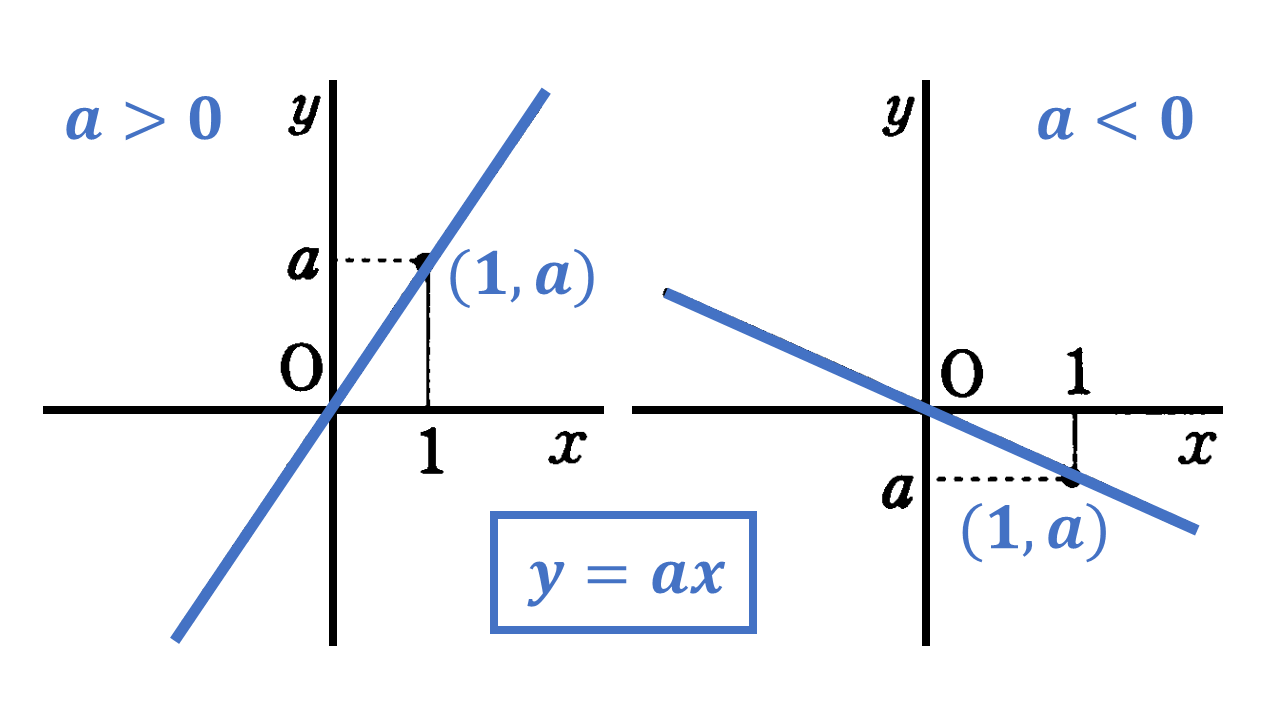
比例 $y=ax$ のグラフ:
(1) 原点 $(x,y)=(0,0)$ を通る直線。
(2) 比例定数が $a>0$ のとき $\to$ 右上がり。
(3) 比例定数が $a<0$ のとき $\to$ 右下がり。
(4) 描き方:原点と他の1点 $(x,y)=(m,n)$ を求めて直線で結ぶ。$x \neq 0$ のとき $\frac{y}{x}=\frac{m}{n}=a$ の値は一定で比例定数 $a$ に等しいため比例の表やグラフが与えられれれば比例の式 $y=ax$ を求められる。また反対に比例の式 $y=ax$ が与えられれば比例の表やグラフを求めることができる。
反比例とそのグラフ
反比例する関係にはどのようなものがあるでしょうか。たとえば道のりが分かっているときに、歩く速さと必要な時間の間には反比例の関係が成り立ちます。距離が決まっている時、速く歩くと必要な時間が短くなるためです。他にも面積が決まっている長方形の縦横の長さの間にも反比例の関係が成り立ちます。このように一方が増加すると他方が減少する関係(トレードオフの関係)は世の中に無数に存在し、また非常に大切な考え方です。本節で正しく理解しておきましょう。
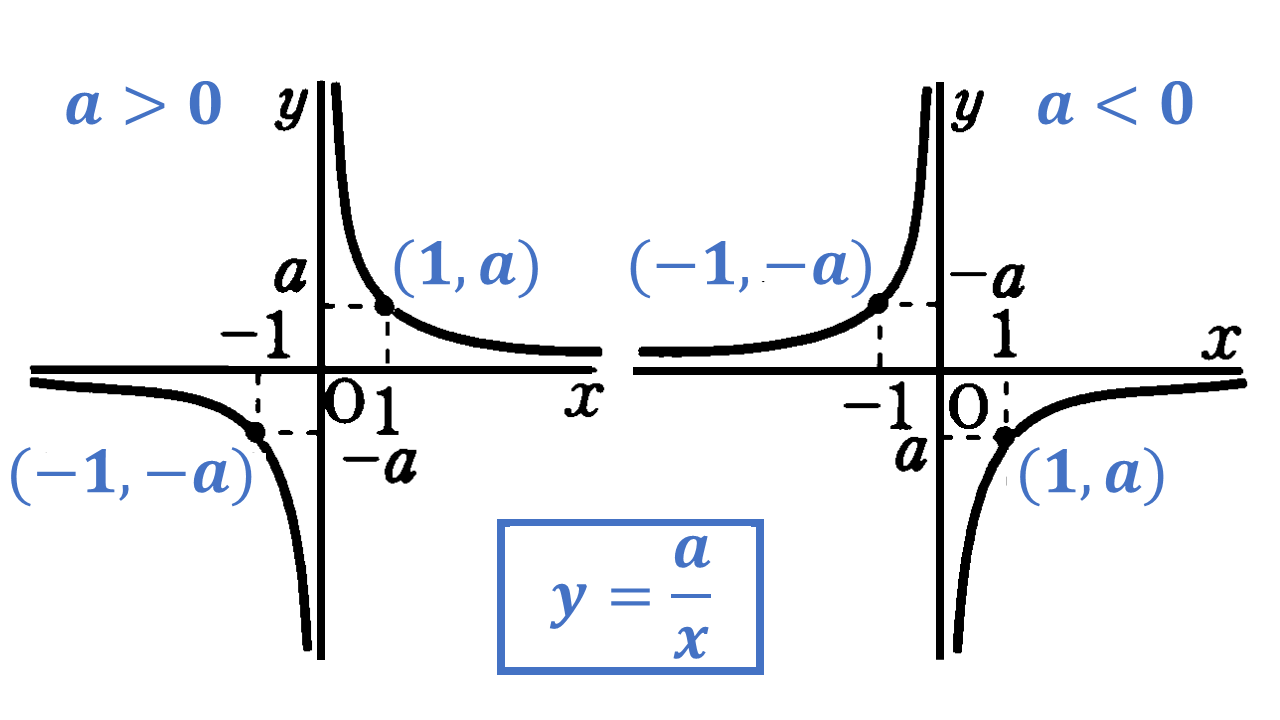
反比例:$y$ は $x$ に反比例 $\to$ $y=\frac{a}{x}$ ($a$は定数, $a \neq 0$, $x \neq 0$) ここで定数 $a$ は比例定数とよばれる(比例の関係の時と同様)。また反比例のグラフはなめらかな2つの曲線となり、この曲線を双曲線という。この $y=\frac{a}{x}$ のグラフは $x$ 軸および $y$ 軸とは交わらない(軸を延長しても交わることはない)。
反比例のグラフ:
(1) 双曲線とよばれる曲線になる。
(2) 原点について点対称である。
(3) 比例定数 $a$ が $a>0$ のとき $\to$ $x$ が増加するとき $y$ は減少する。
(4) 比例定数 $a$ が $a<0$ のとき $\to$ $x$ が増加するとき $y$ も増加する。
(5) 描き方:点 $(x,y)=(m,n)$ が得られたとき $xy=mn=a$ の値は一定で比例定数 $a$ に等しいため反比例の表やグラフが与えられれれば反比例の式 $y=\frac{a}{x}$ を求められる。また反対に反比例の式 $y=\frac{a}{x}$ が与えられれば反比例の表やグラフを求めることができる。
比例と反比例の利用
身近な問題を比例や反比例の関係を利用して解決してみましょう。(1) 紙束の枚数を重さから計算したり (2) 決まった量の課題を制限時間内にグループで終わらすために必要な人数を求めたり (3) 地震の揺れを予測したり (4) 自転車の変速機の仕組みを調査したり…これまでに学んだ知識を活用して、自由に問題を解決してみましょう。
※ (1) は比例の関係:1枚の重さが$5$gだったとすると、紙束の枚数を $y$ 枚、重さを $x$gとすれば $y=\frac{x}{5}$ の関係式から紙束の枚数を計算できる。(2) は反比例の関係:課題が100ページの数学ドリルで、時間何に1人あたりが終わらすページ数を $x$ ページ、グループの人数を $y$ 人とすると $xy=100$ となり反比例の関係が得られ $y=\frac{100}{x}$ の関係式から必要な人数を計算できる。(3) は比例の関係:地震の揺れを伝える波(P波とS波)の伝達速度からどの場所でいつ地震が発生するかを予測することができる(緊急地震速報のシステムなど)。 (4) はギアの歯の数の比に注目して自由に考えてみましょう。
ともなって変わる3つの変数 $x,y,z$ があって関係 $z=xy$ が成り立つとき:
(1) $x$ が一定なら $z$ は $y$ に比例する( $z=ay$ ($a$ は定数))。$y$ が一定なら $z$ は $x$ に比例する( $z=ax$ ($a$ は定数))。
(2) $z$ が一定なら $y$ は $x$ に反比例する( $y=\frac{a}{x}$ ($a$は定数))。$x$は$y$に反比例する($x=\frac{a}{y}$ ($a$は定数))。
中1 > 5章:平面図形
この章では合同や対称という見方で平面の図形の性質を調べたり、図形を移動させたり、正確な図形を作図する方法などについて学びます。また様々な図形に触れて、その性質について理解を深めましょう。そうすることで、身近な模様に対する新たな見方もできるようになり、数学の世界の広がりを感じることができるでしょう。
数学が面白くなる動画―6
実はすごい六角形の秘密。ハチの巣はなぜ六角形なのでしょうか?
数学が面白くなる動画―7
なぜマンホールは丸いのでしょうか?丸以外の形のマンホールだとどうなるのか考えてみましょう。
直線と角
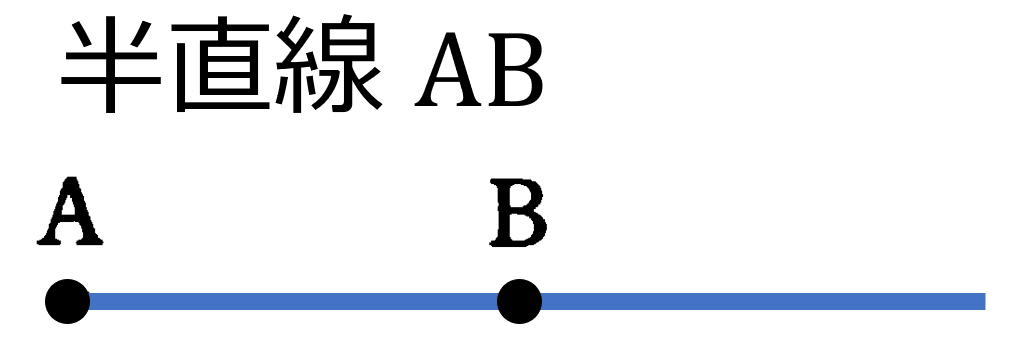
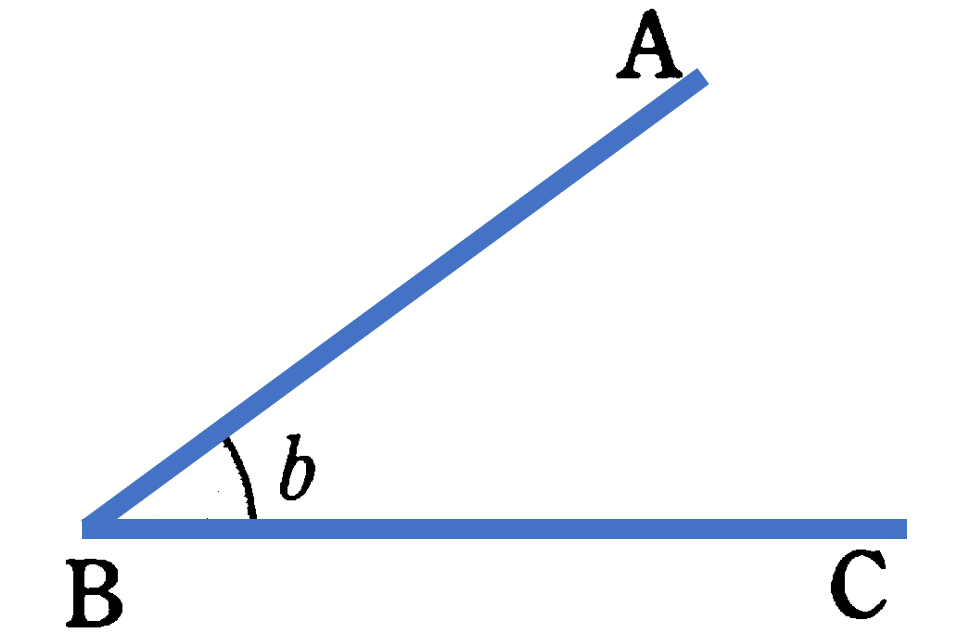
本節では直線と角の考え方を理解します。直線はふつう両方に限りなくのびているものとして考えます。2点 ${\rm A}$, ${\rm B}$ を通る直線は1つしかひけず直線 ${\rm AB}$といいます。また直線 ${\rm AB}$ のうちの2点 ${\rm A}$, ${\rm B}$ の間の部分を線分 ${\rm AB}$ といいます。これまで意識することはなかったかもしれませんが、三角形の辺や円の直径などは「線分」です(線分 ${\rm AB}$ を ${\rm B}$ の方へまっすぐ限りなく伸ばしたものを半直線 ${\rm AB}$ といいます)。三角形 ${\rm ABC}$ は記号を使って ${\rm \triangle{ABC}}$ と表します。また平行な2直線を平行線といい、2直線 ${\rm AB}$, ${\rm AB}$ が平行であることを記号を用いて ${\rm AB}/ \! \! /{\rm CD}$ とかきます。平行線は角を作りませんが、たとえば1つの点 $O$ から出る半直線 ${\rm OA}$, ${\rm OB}$ は角を作ります。この角を記号を使って $\angle {\rm AOB}$ と表して「角 ${\rm AOB}$」と読みます。また角の大きさが等しいことを等号を用いて、たとえば $\angle {\rm AOB} = \angle {\rm BOA}$ のように書きます。さらに、2直線が垂直であるとき、一方の直線を他方の直線の垂線といいます。線分 ${\rm AB}$ と直線 ${\rm \ell}$ が垂直であることを記号を使って ${\rm AB} \perp {\rm \ell}$ とかきます。そして線分を2等分する点を中点といい、中点を通り、その線分に垂直な直線を垂直二等分線といいます。これらの記号や用語を正しく理解し、線や角に関して、定義に従った正しい言葉で線の説明をできるようになりましょう。
直線:2点で定まる。

線分:両端のあるもの。

半直線:一端だけのあるもの。
角:$\angle {\rm ABC}$の大きさを$\angle {\rm ABC}$,$\angle {\rm B}$,$\angle b$で表す。
2直線の垂直・平行:
(1) 垂直 $ \ell \perp m$:2直線 $ \ell, m $ が垂直に交わる。
(2) 平行 $ \ell / \! \! / m$:2直線 $ \ell, m $ が交わらない。
距離:「最短」の線分の長さのこと。
(1) 2点間の距離:2点を結ぶ線分の長さ。
(2) 点と直線の距離:点から直線にひいた垂線の長さ。
(3) 平行線の距離:平行な2直線の一方の上にある点と他方の直線との距離。
図形の移動
ある図形を形や大きさを変えずにほかの位置に移すことを移動といいます。本節では図形の移動を理解・利用して、様々な問題について考えてみましょう。
平行移動:図形を一定の方向に一定の距離だけずらす移動。
平行移動の性質:対応する点を結ぶ線分は平行で長さが等しい。
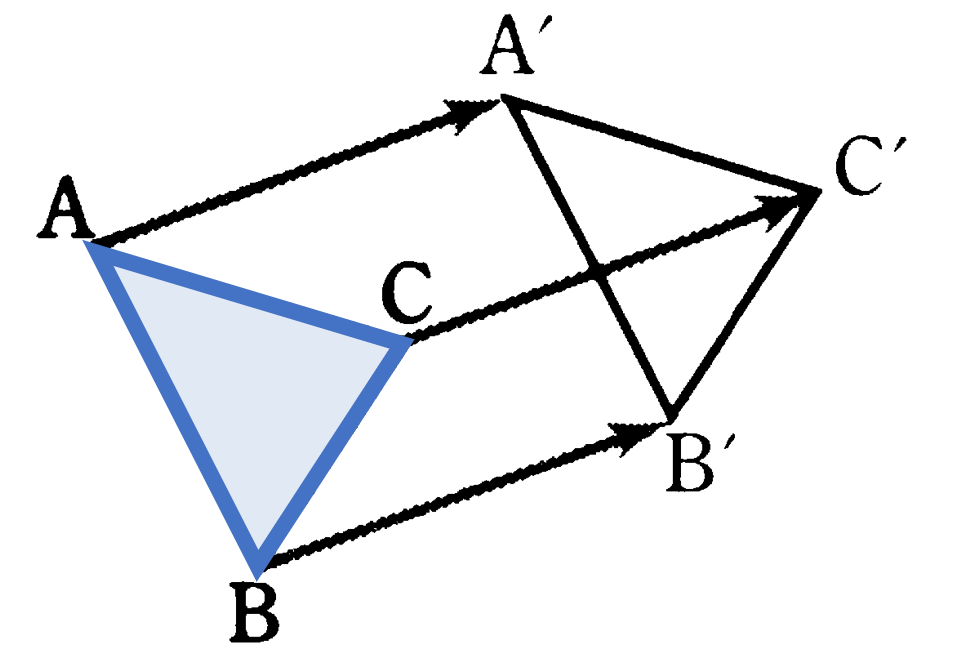
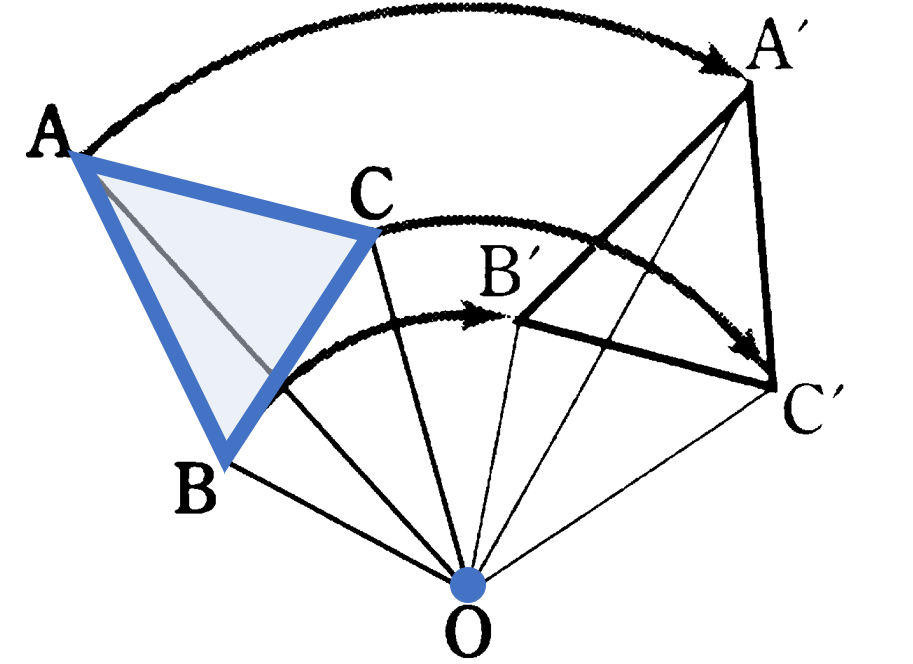
回転移動:図形をある点 $O$ を中心にして一定の角度だけ回転させる移動。中心とする点 $O$ は回転の中心という。
回転移動の性質:対応する点は回転の中心から等しい距離にあり、対応する点と回転の中心とを結んでできる角の大きさが全て等しい。
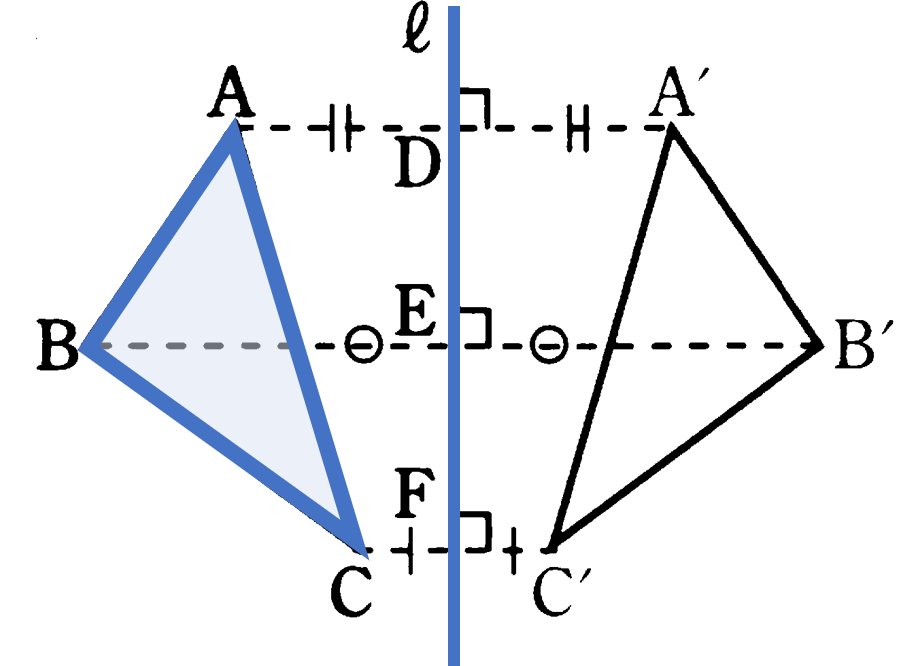
対称移動:図形を1つの直線 $\ell$ を折り目として折り返す移動。直線 $\ell$ を対称の軸という。
対称移動の性質:対称の軸は対応する2点を結ぶ線分の垂直二等分線になる。
作図
あなたの筆箱には何が入っているでしょうか。本節では定規とコンパスだけを使って、どんな図形がかけるかを考えます。これらの2つの簡単な道具を工夫して使うことで、驚くほど多様な図形を描くことができるようになります。そのためにも、作図の工程のひとつひとつの意味を正確に理解していきましょう。
作図:定規とコンパスだけを用いて図形を描くことを「作図」という。定規は直線をひくために、コンパスは円をかくために用いる。またコンパスは等しい長さをとったり、線分を移したりすることができる。また作図のためにかいた「必要な線」は消さない。
線分の垂直二等分線・中点
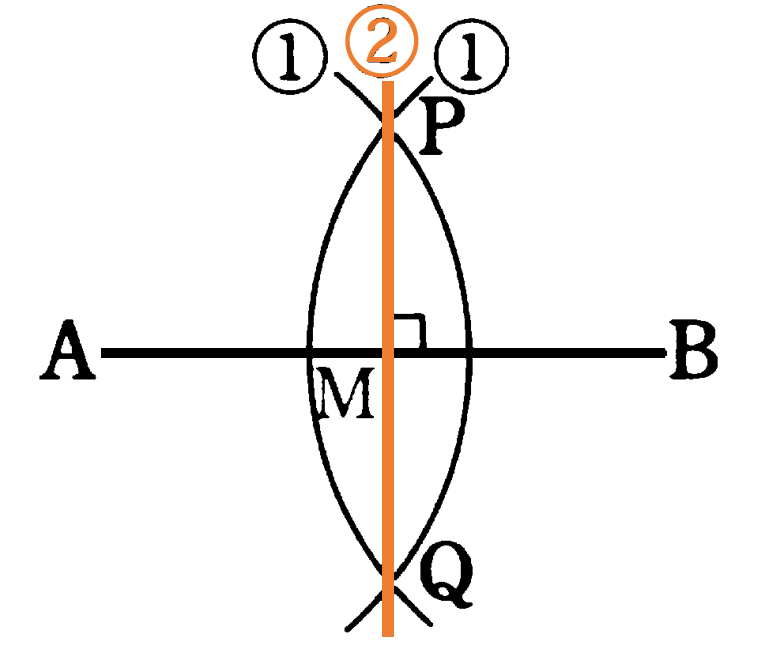
※ 線分の両端の点を中心に、等しい半径の円を2つかき、その2つの円上にできる2つの交点を結ぶことで、線分の垂直二等分線をかくことができる。垂直二等分線が、2つの点から距離が等しい点の集まりであることを理解していれば、この作図方法を理解しやすい。
角の二等分線
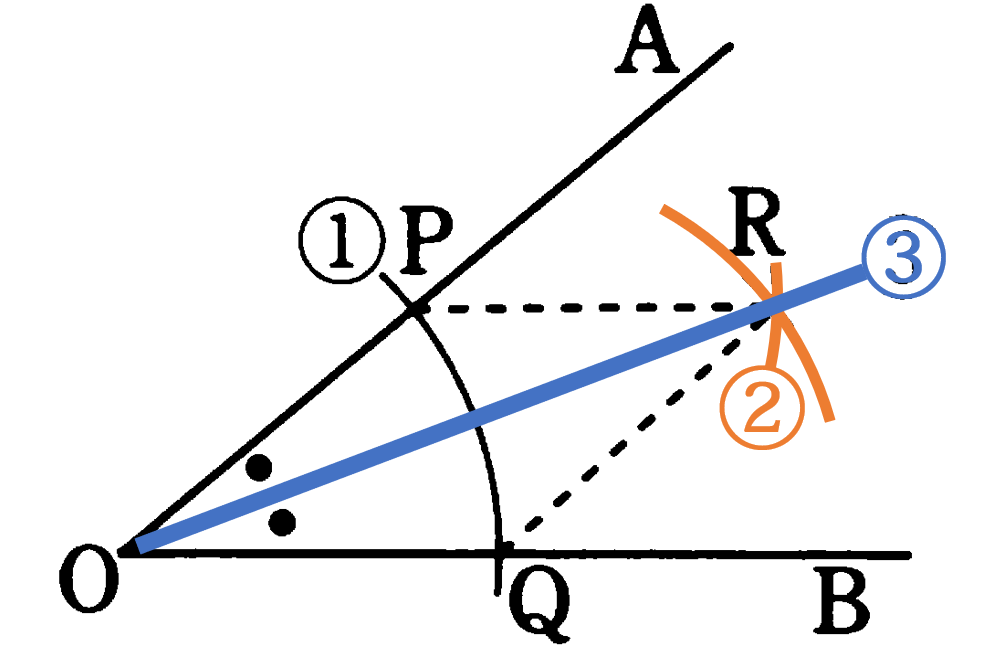
※ 1つの角を2等分する半直線を、その角の二等分線という。角の二等分線上のどの点をとっても、角の2辺までの距離が等しく点の集まりであることを理解していれば、この作図方法を理解しやすい。
直線への垂線
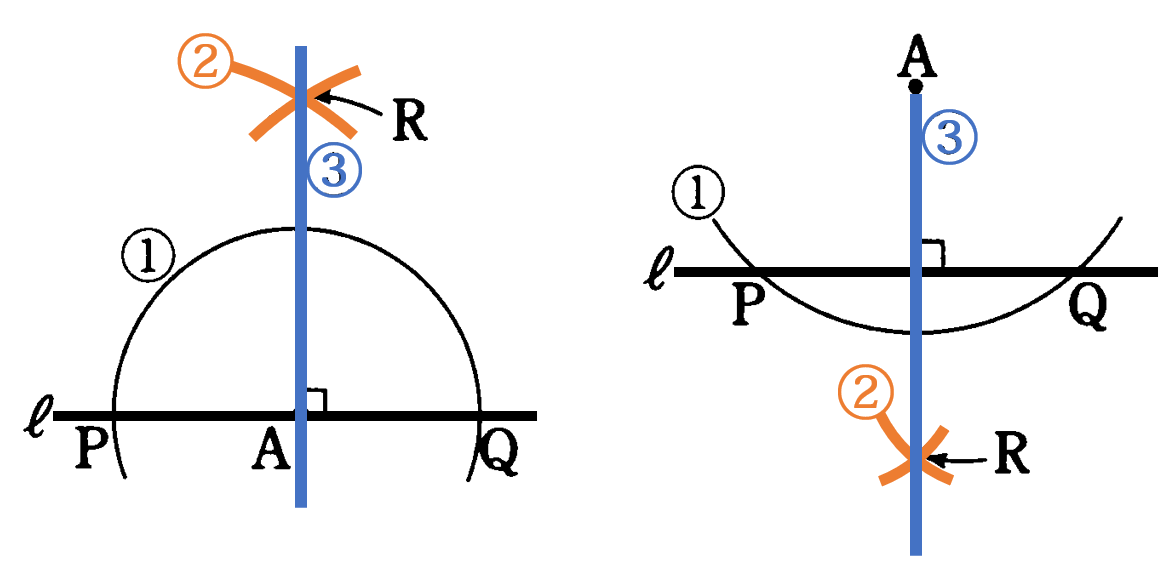
※ 直線への垂線が、直線上のある2点から等しい距離にある点の集まりであることを理解していれば、この作図方法を理解しやすい。
円と作図:
(1) 弧:円周上の2点をA,BとするときAからBまでの円周の部分を弧 ${\rm AB}$ といい $\stackrel{\frown}{AB}$ と表す。
(2) 弦:円周上の2点を結ぶ線分を弦といい、両端がA,Bである弦を弦 ${\rm AB}$ という。
(3) 接する:直線が1点だけで円と交わる場合を、直線が円に接するといい、この直線を接線、円と直線とが接する点を接点という。
(4) 円の接線:円の接線は接点を通る半径に垂直。円の接線が、接線を対称の軸として移動させた円の中心と元の円の中心の2点から等しい距離にある点の集まりであることを理解していれば作図できる。
いろいろな作図:
(1) 点を決めるには2直線や2円の交点や直線と円の交点とする。
(2) 直線を決めるには通る2点を選ぶ。
円とおうぎ形
車のワイパーがふき取る部分の形や扇子の形、日本の伝統模様の「青海波」の柄など、目にする機会が多いおうぎ形。おうぎ形は円の一部で、弧の両端の点を通る2つの半径(2つの線分)とその弧で囲まれた図形です。おうぎ形で、2つの半径のつくる角を中心角といいます。本節では、おうぎ形の弧の長さや面積などの特徴について理解しましょう。
半径 $r$ の円:周の長さ $\ell=2 \pi r$, 面積 $S=\pi r^2$
半径 $r$ 中心角 $a^\circ$ のおうぎ形:弧の長さ $\ell=2 \pi r \times \frac{a}{360}$, 面積 $S=\pi r^2 \times \frac{a}{360}=\frac{1}{2}\ell r$
※ 1つの円(半径 $r$ が決められた時)ではおうぎ形の弧の長さと面積は中心角の大きさに比例する。
中1 > 6章:空間図形
本章では図形の見方を「平面の世界(2D)」から「空間の世界(3D)」に変えて考えてみます。身の周りには形に着目すると様々な立体としてみることができるものがあります。たとえば四角いビルは直方体、電信柱は円柱、バレーボールは球として分類することができます。世の中にはどのような形があるかを学び、その特徴について考えていきましょう。
数学が面白くなる動画―8
空間上の位置(地図の上では座標 $(x,y)$ )を正確に測定するGPSのしくみ。
いろいろな立体
いろいろな立体を比べて、その共通点や違いについて考えましょう。たとえば、平面だけで囲まれた立体は多面体と呼ばれます。多面体は、その面の数によって、四面体や八面体などといいます。他にも角柱や角錐、円錐や正多面体など、様々な立体があり、それぞれ特徴があります。その特徴と立体の名前を正しく理解し、空間図形の理解の基礎知識をしっかりと身につけましょう。
正多面体:どの面もすべて合同な正多角形であり、どの頂点にも面が同じ数だけ集まっている、へこみのない多面体。正四面体・正六面体(立方体)・正八面体・正十二面体・正二十面体の5種類。
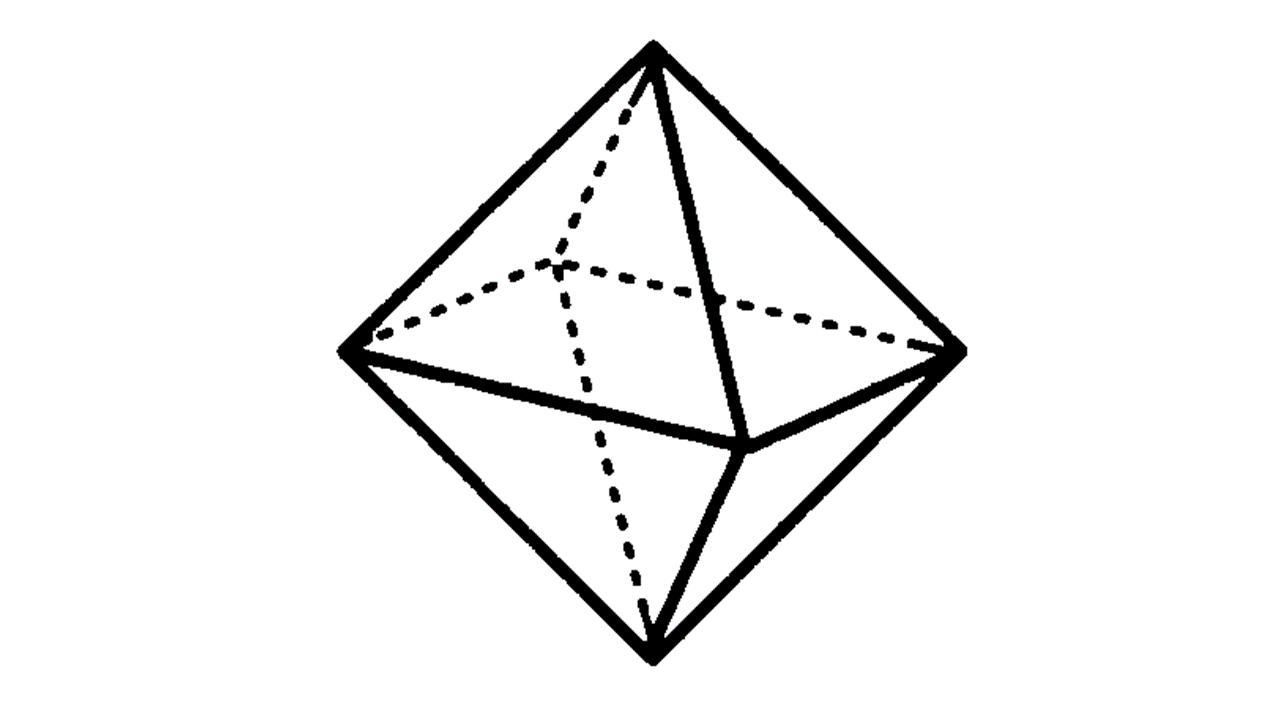
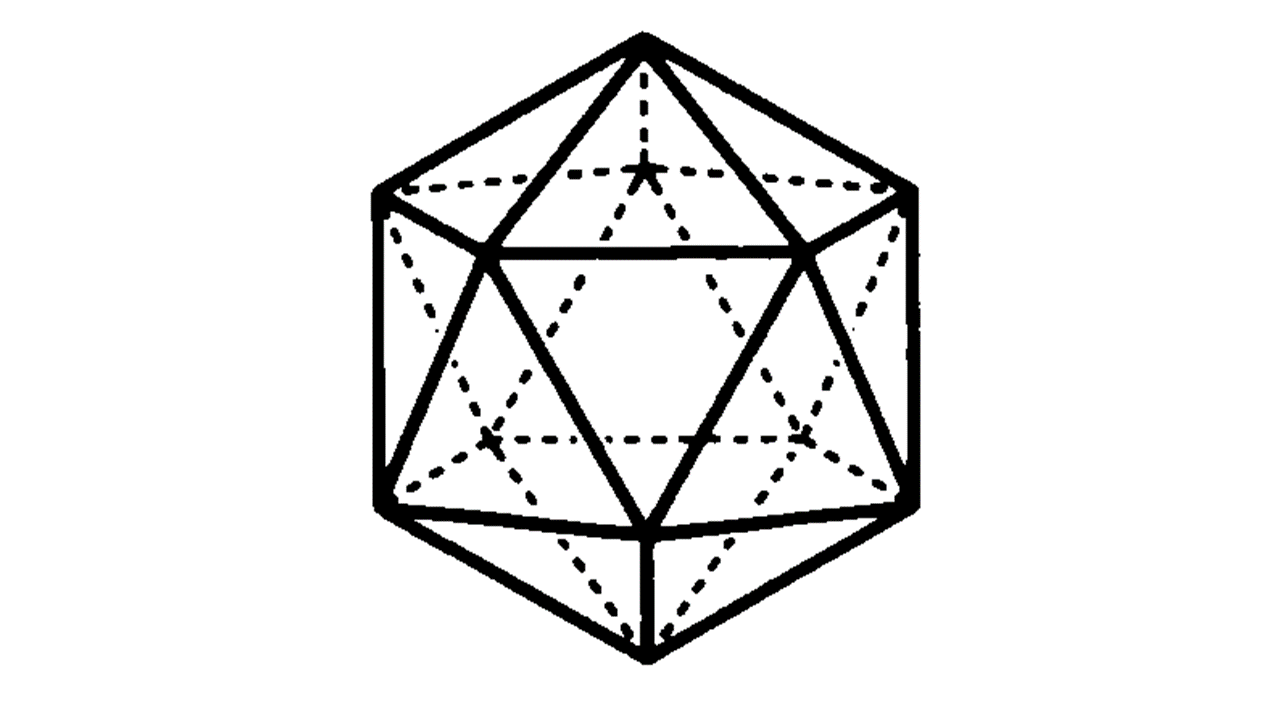
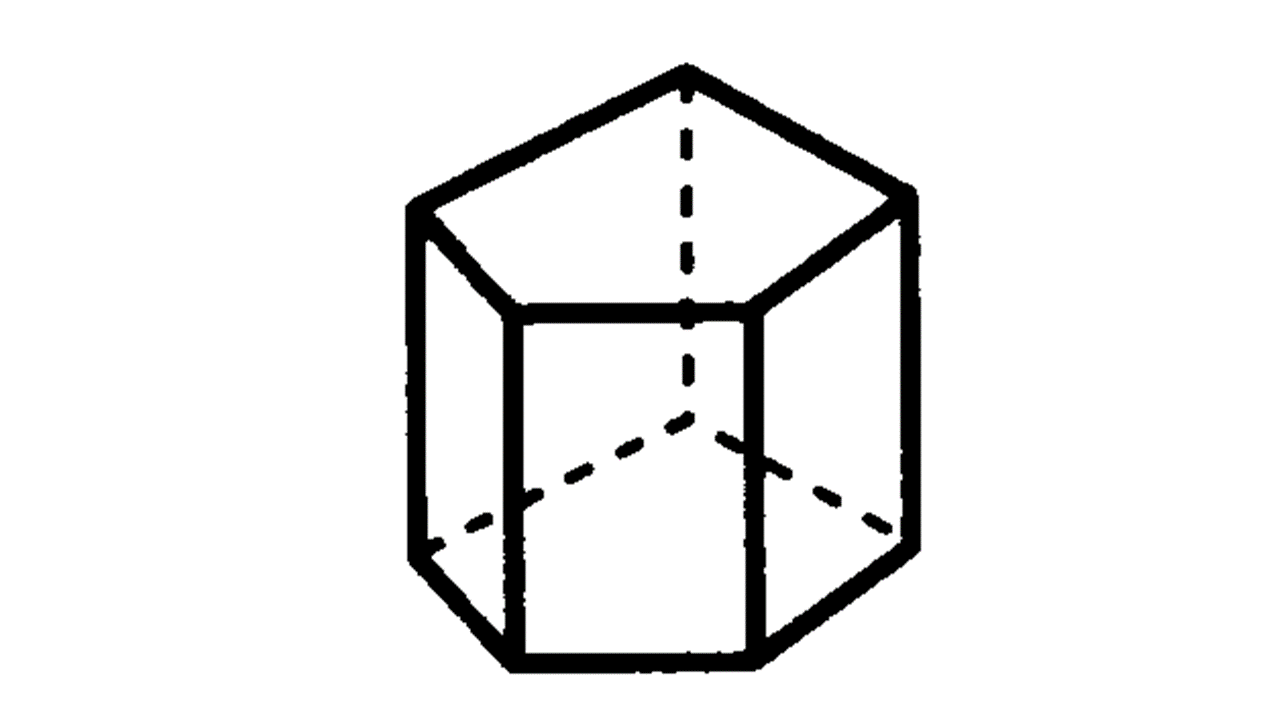
角柱・角錐・円柱・円錐
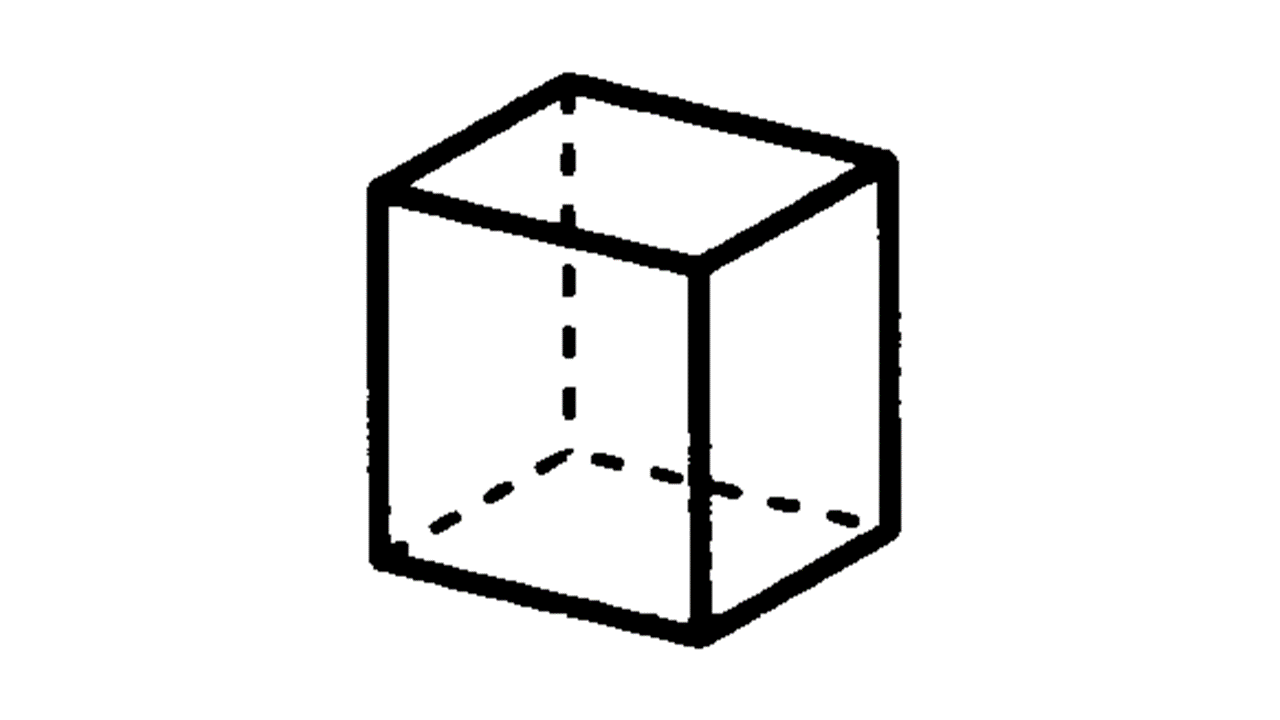
(1) 角柱:柱状で、底面が三角形の場合は三角柱、四角形の場合は四角柱、長方形(もしくは正方形)のときは直方体となる。底面が正方形で高さが正方形の1辺の長さに等しい場合は立方体となる。また、底面が正三角形で側面がすべて合同な長方形である角柱を正三角柱、底面が正方形で側面がすべて合同な長方形である角柱を正四角柱という。
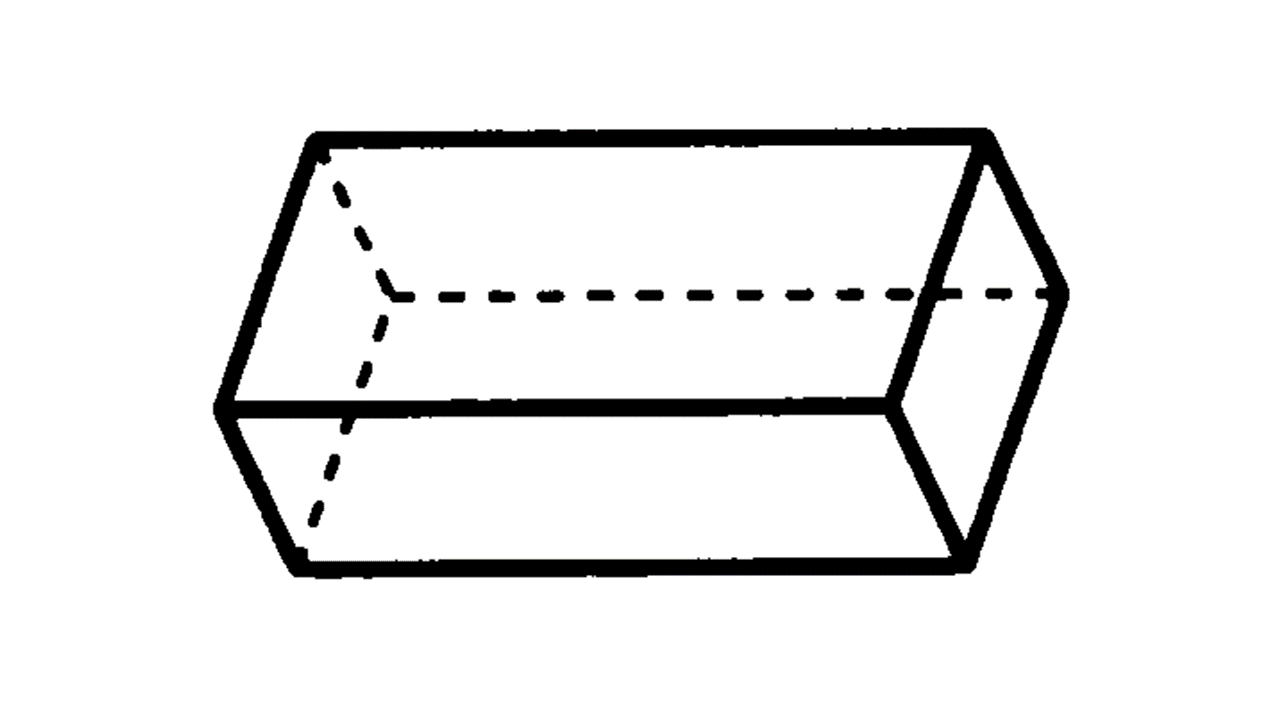
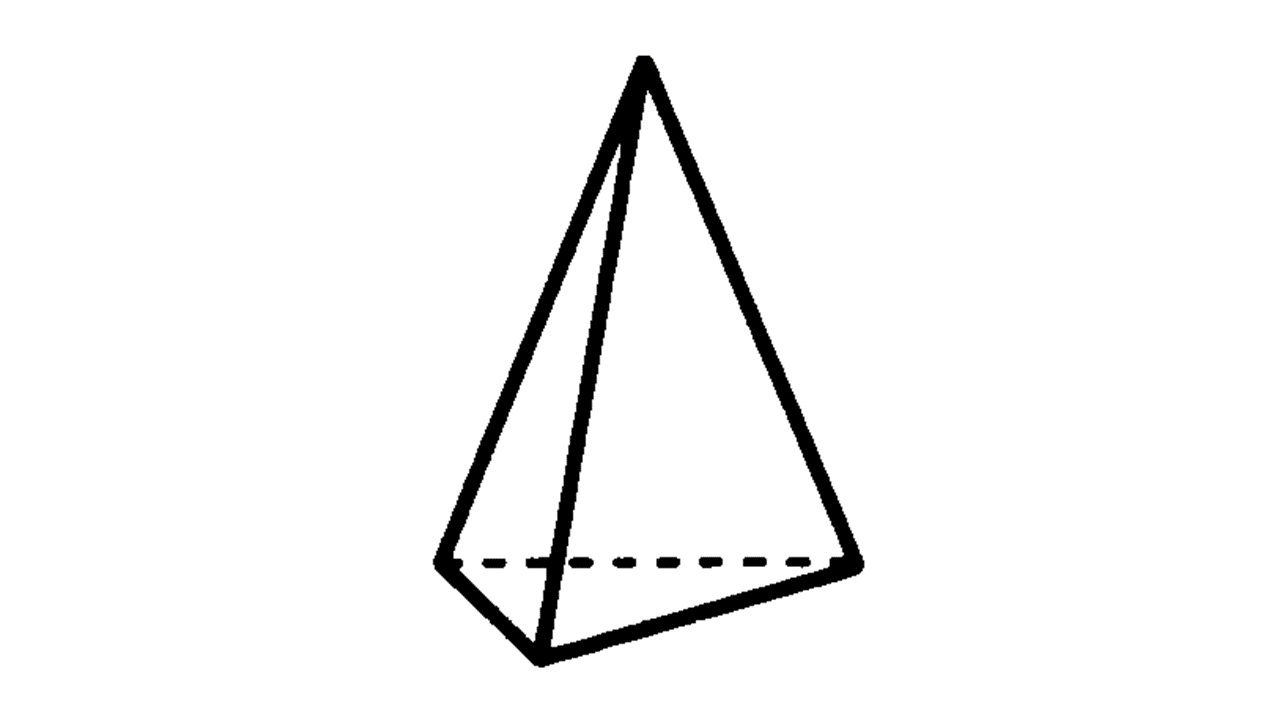
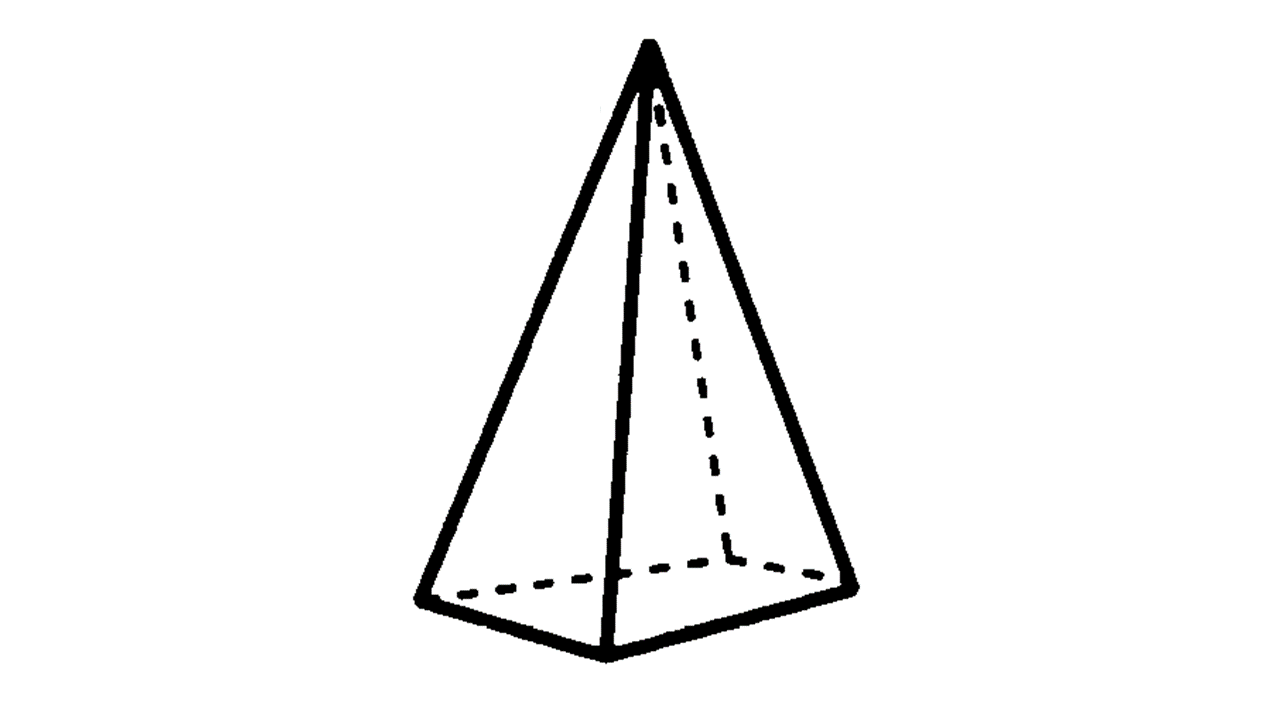
(2) 角錐:底面が三角形の場合は三角錐、四角形の時は四角錐となる。また、底面が正三角形で側面がすべて合同な二等辺三角形である角錐を正三角錐、底面が正方形で側面がすべて合同な二等辺三角形である角錐を正四角錐という。
(3) 円柱:柱状で底面が円になっている立体を円柱という。
(4) 円錐:底面が円になっている錐体(※数学用語)を円錐という。
※ おまけ:オイラーの多面体定理:多面体の面や辺や頂点の数を計算するときに利用できる公式。多面体の「頂点」「辺」「面」の数について (頂点の数) $-$ (辺の数) $+$ (面の数) $=2$ が成り立つ。
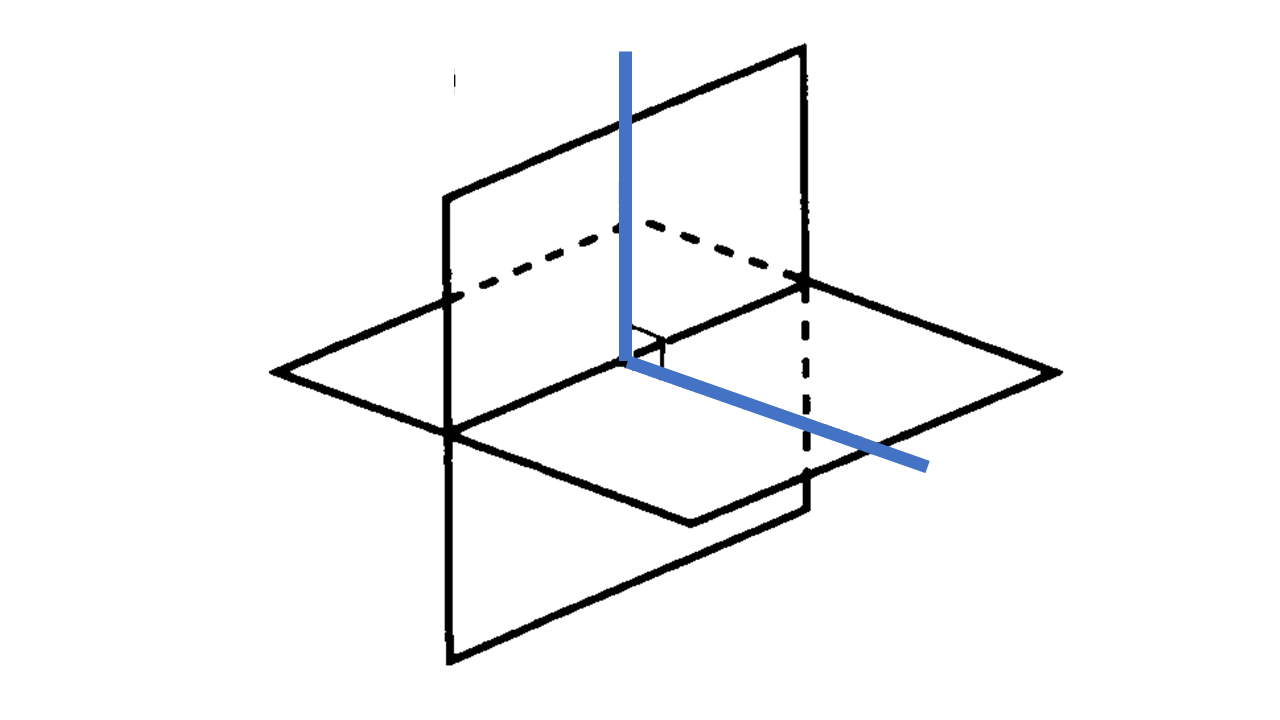
直線や平面の位置関係
空間図形をとらえたり表現したりするためには、それをどの方向から見ているかなどの「位置関係」を明らかにする必要があります。そのために、空間における直線や平面の位置関係について考えてみましょう(ここでいう平面とは、両方に限りなく伸びている直線のように、限りなく広がっているものを考えます)。
平面の決定:以下の(1)~(4)のいずれかが空間に存在するときそれらを含む平面は1つに定まる。
(1) 同じ直線上にない3点。
(2) 交わる2直線。
(3) 平行な2直線。
(4) 1直線とその上にない1点。
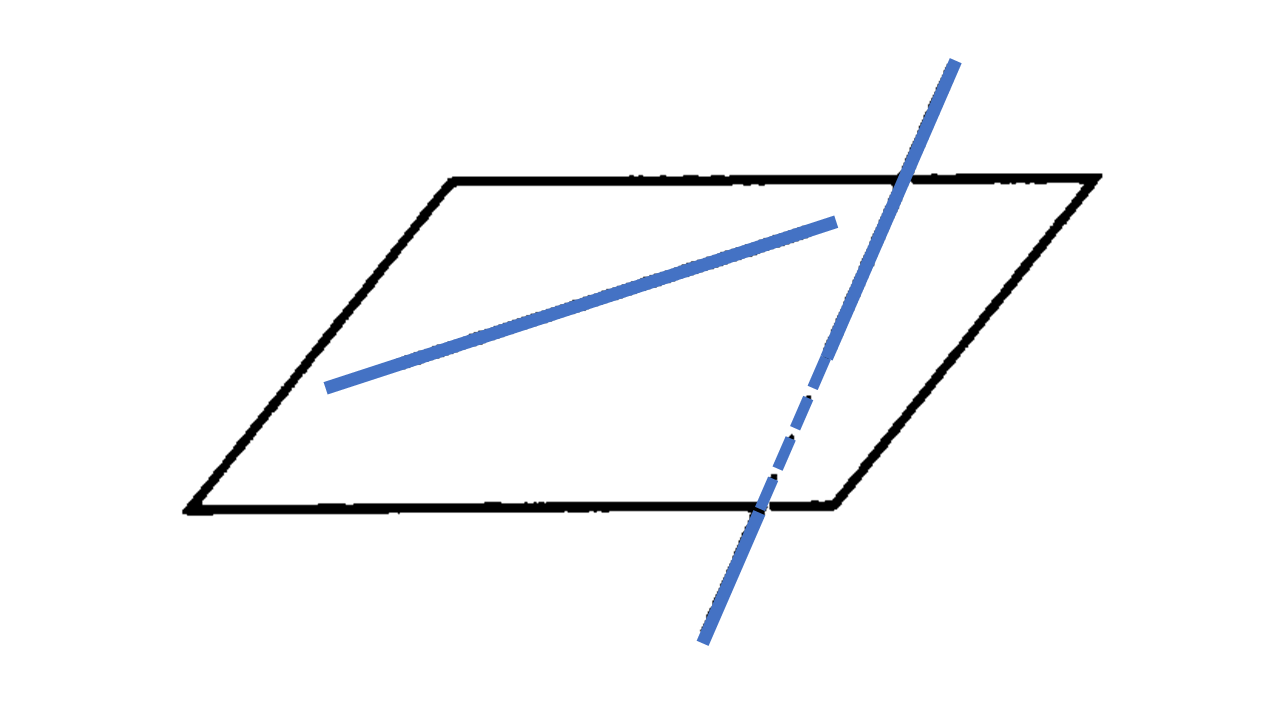
2直線の位置関係:空間内にある2つの直線は、交わる場合と交わらない場合がある(平面図形では、交わらない2つの直線は平行である)。空間内で平行でなく交わらない2直線はねじれの位置にあるという。以上のことより2直線の位置関係は以下の(1)(2)のいずれかで表される。
(1) 同じ平面上にある $\to$ (A) 交わる。 (B) 平行である。
(2) 同じ平面上にない $\to$ ねじれの位置にある。
直線と平面の位置関係:直線と平面の位置関係は以下の(1)~(3)のいずれかで表される。
(1) 直線が平面に含まれる。直線が平面上にあるともいう。
(2) 1点で交わる。
(3) 交わらない(直線を $\ell$ 平面を ${\rm P}$ とすると $\ell/ \! \! /{\rm P}$)。
2平面の位置関係:平面と平面が交わったところにできる線は直線となり、この線を交線という。2平面の位置関係は以下の(1)(2)のいずれかで表される。
(1) 交わる。
(2) 交わらない(平行である。2つの平面をそれぞれ ${\rm P,Q}$ とすると ${\rm P}/ \! \! /{\rm Q}$)。
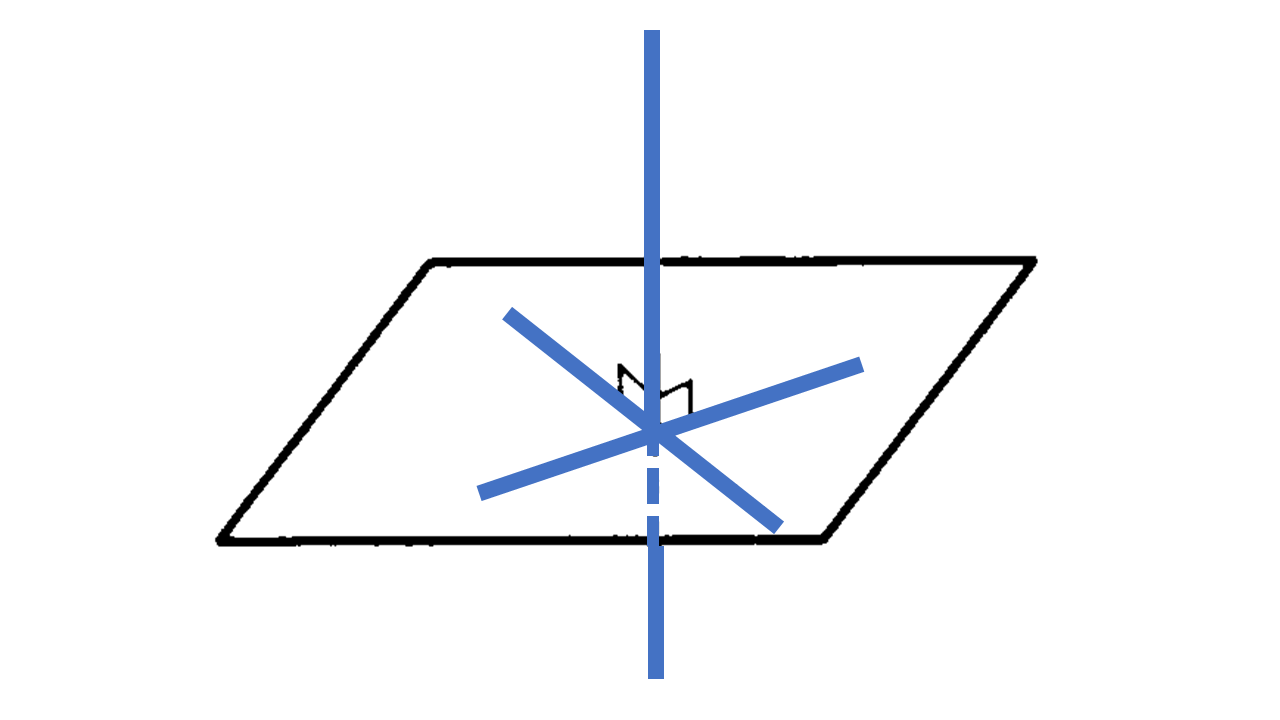
直線と平面の垂直:平面 ${\rm P}$ に対してどの方向にも傾いていない直線 $\ell$ を考える。このとき $\ell$ は ${\rm P}$ との交点 ${\rm O}$ を通る ${\rm P}$ 上のどの直線にも垂直になっている。このようなとき、直線 $\ell$ は平面 ${\rm P}$ に垂直であるという(垂直が成り立つ最小の条件としては、平面 ${\rm P}$ と交わる直線 $\ell$ がその交点 ${\rm O}$ を通る ${\rm P}$ 上の2つの直線 $m,n$ に垂直になっていれば、直線 $\ell$ は平面 ${\rm P}$ に垂直であるといえる)。
点と平面との距離:1つの点 ${\rm A}$ から平面 ${\rm P}$ に引いた垂線と、平面 ${\rm P}$ との交点を ${\rm H}$ とするとき、線分 ${\rm AH}$ の長さを点 ${\rm A}$ と平面 ${\rm P}$ との距離という。
2平面の垂直:2つの平面 ${\rm P,Q}$ が交わり、この交線 $\ell$ とするとき、 ${\rm P}$ と ${\rm Q}$ のつくる角を考える。平面 ${\rm P,Q}$ のつくる角は、その交線 $\ell$ 上の点で、それぞれの平面上に引いた2つの垂線のつくる角のことである。特に、2つの平面 ${\rm P,Q}$ のつくる角が直角の時、その2つの平面 ${\rm P,Q}$ は垂直であるといい ${\rm P} \perp {\rm Q}$ と表す。
立体の構成
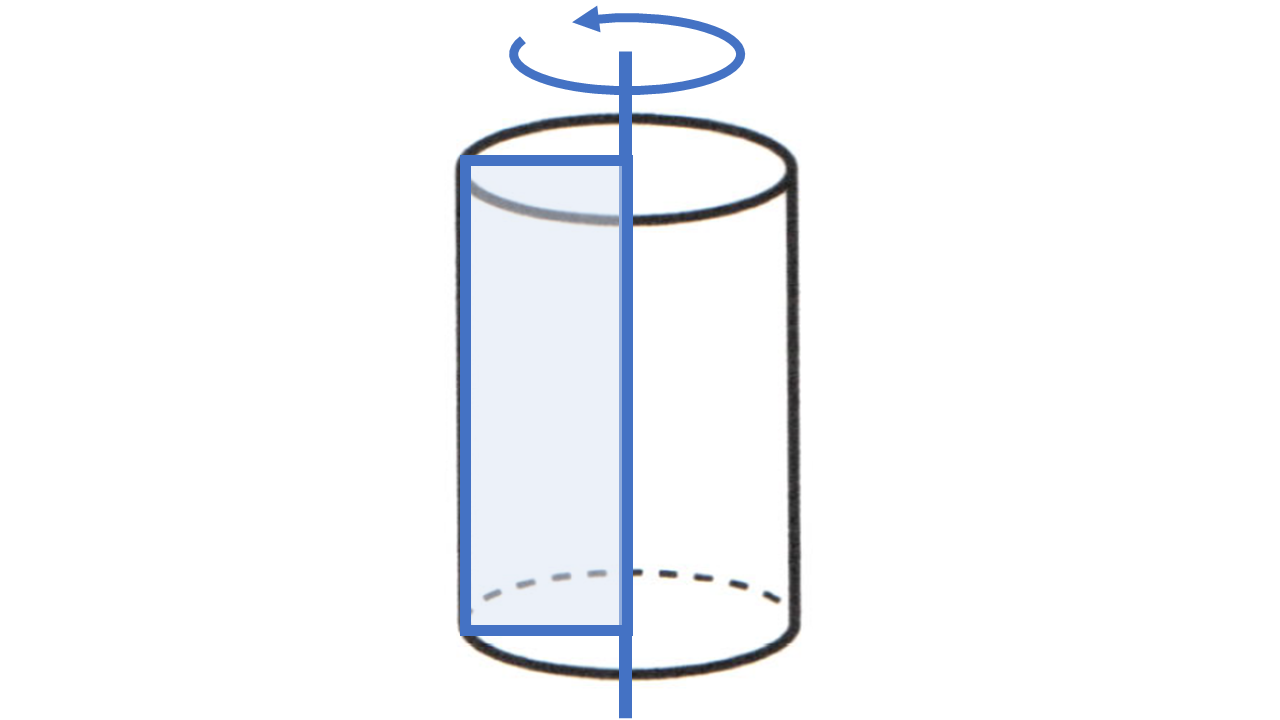
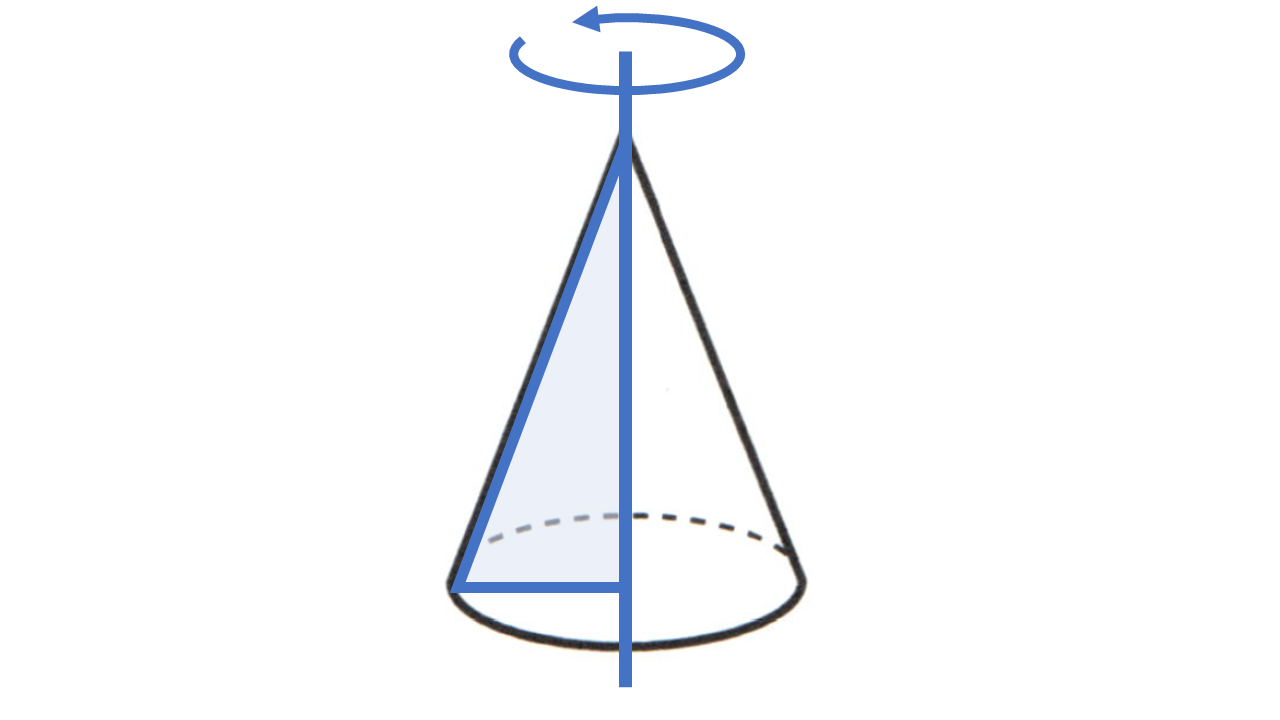
本節では、空間図形を「面の移動」という見方で見ていきます。例えば点が動くことによって線ができ、線が動くことによって面ができます。さらに、面が動くときに立体ができます。特に、円柱や円錐は、それぞれ長方形や直角三角形を「回転させてできた立体」だと考えることができます。このとき、円柱や円錐の側面を描く辺を母線といいます。また円柱や円錐のように、1つの直線を軸として平面図形を回転させてできる立体を回転体といいます。球は半円をその直径を回転の軸として回転させた回転体だと考えることができます。他にも、立体の展開図の特徴を理解することで、より深く空間図形について考えていきましょう。
回転体:
(1) 円柱:回転させる図形 $\to$ 長方形:回転の軸 $\to$ 1辺
(2) 円錐:回転させる図形 $\to$ 直角三角形:回転の軸 $\to$ 直角をはさむ辺
(3) 球:回転させる図形 $\to$ 半円:回転の軸 $\to$ 直径
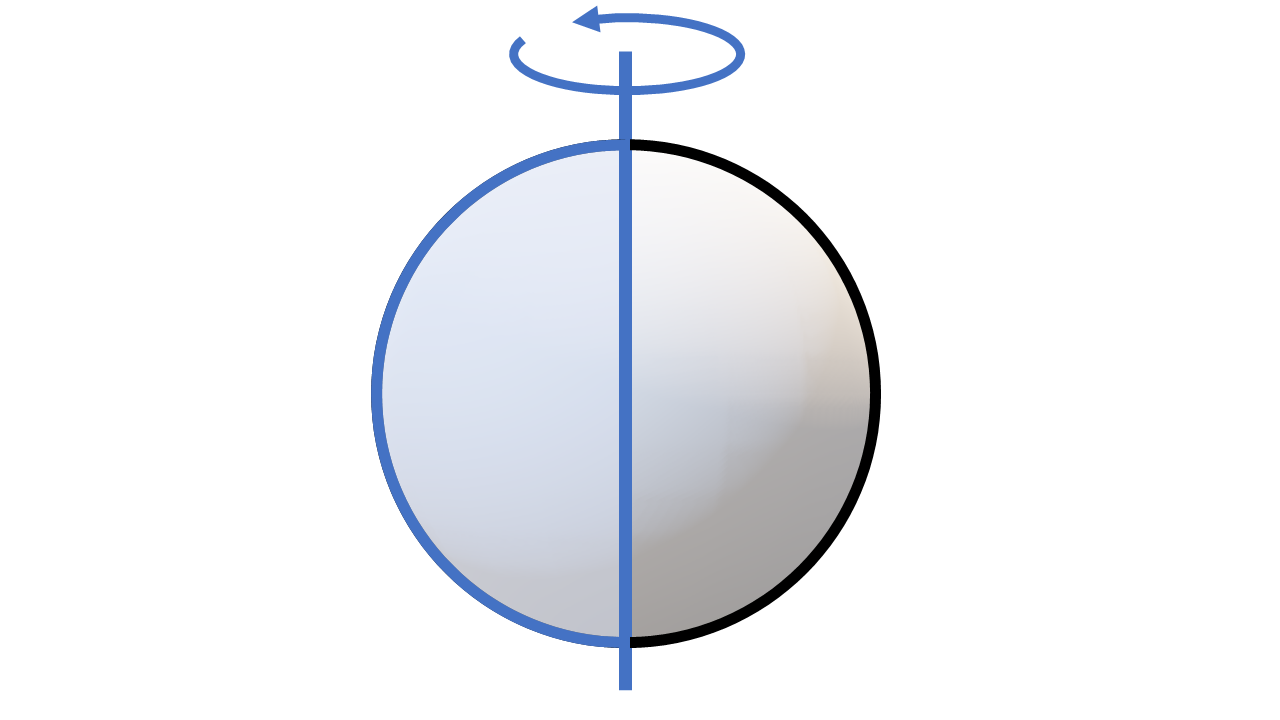
回転体の性質:
(1) 回転の軸に垂直な平面で切ると切り口は円となる。
(2) 回転の軸を含む平面で切ると切り口は回転の軸について対称な図形になる。
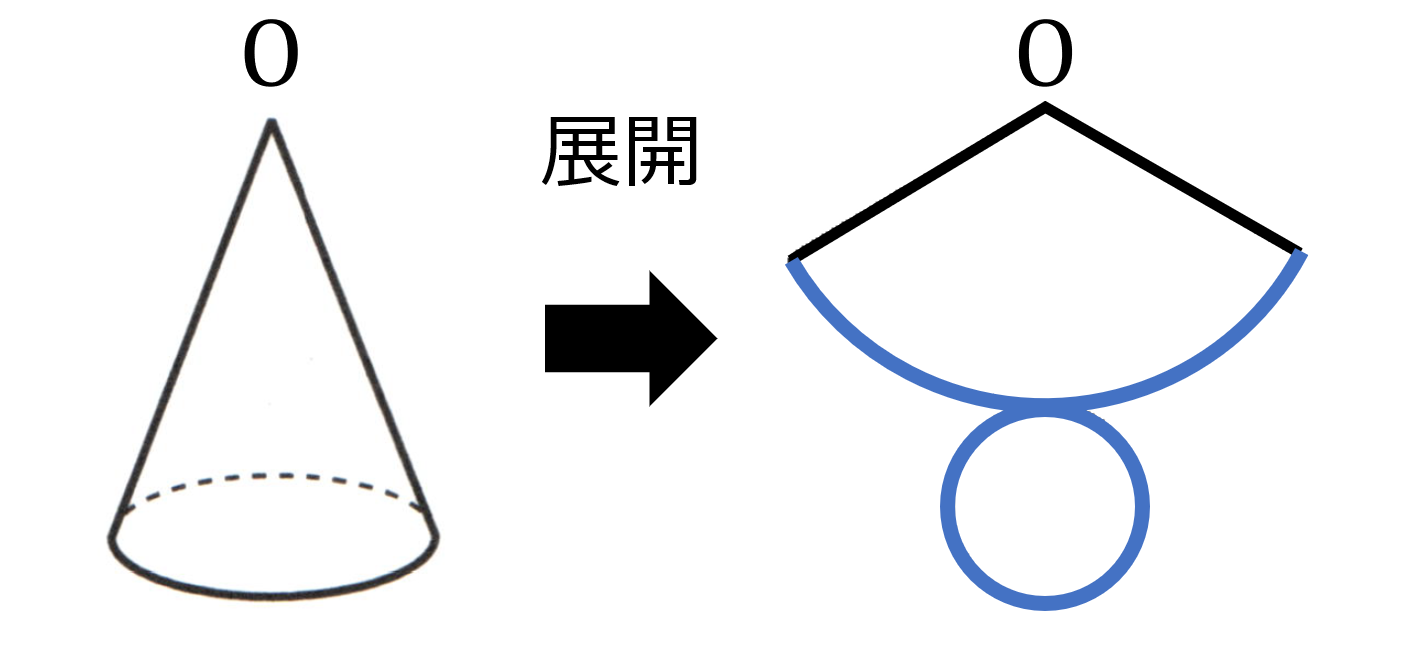
立体の展開図:立体の展開図では、立体でのすべての辺や面積の形や大きさが表現される。特に特徴的なのが円錐の展開図である。円錐の展開図は側面がおうぎ形、底面が円となる。おうぎ形の弧の長さは底面の円周に等しい。また、おうぎ形の半径は円錐の母線に等しい。
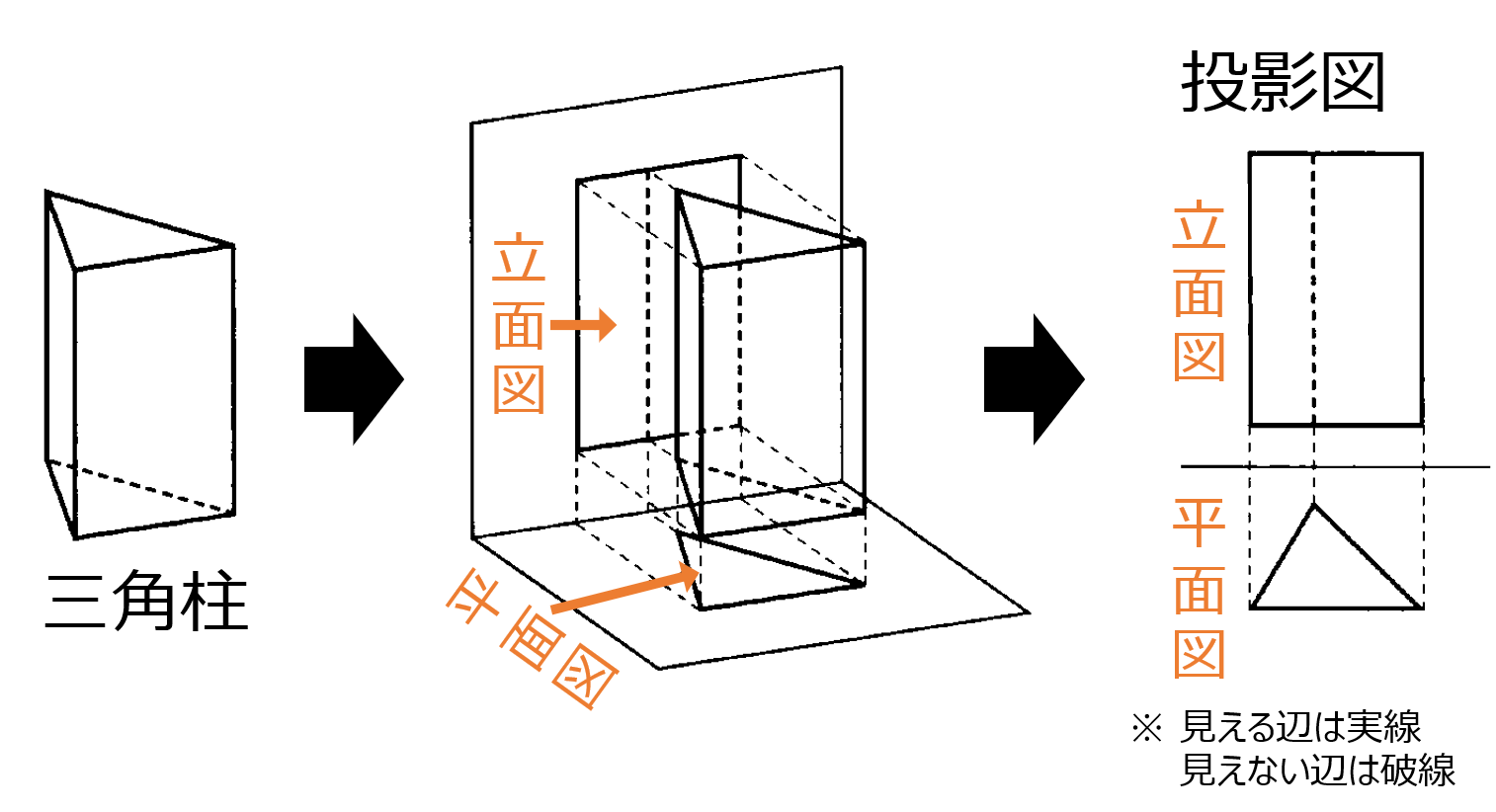
立体の投影図:立体を平面としてあらわす方法の一つ(他に見取りや展開図等がある)。立体をある方向から見て平面に表した図を投影図という。立体を真上から見た図を平面図、正面から見た図を立面図といい、立体を投影図で表現する場合、平面図と立面図を用いて表すことが多い(立体の形が読み取れない場合は横から見た図を加えることもある)。
立体の表面積と体積
例えば牛乳パックの多くは直方体、コップは円柱、パフェなどの容器は円錐などの立体としてみることができます。本節では、身の周りの容器(立体)の容積(体積)や表面積などを求める方法について考えましょう。
表面積:立体の全ての面の面積の和を表面積という。また側面全体の面積を側面積、1つの底面の面積を底面積という。
(1) 角柱・円柱の表面積 $=$ 底面積 $\times 2 +$ 側面積
(2) 角錐・円錐の表面積 $=$ 底面積 $+$ 側面積
※ おうぎ形の面積:円錐の表面積の計算でおうぎ形の面積の計算が必要になる。半径 $r$ 弧の長さ $\ell$ のおうぎ形の面積 $S$ は $S=\frac{1}{2} \ell r$ で求められる(おうぎ形を細長いおうぎ形に細かく分けたもののうちの半分を逆さまにして組み合わせると、2辺の長さがそれぞれ $\frac{1}{2} \ell$, $r$ の長方形になることから確認できる)。
(3) 半径 $r$ の球の表面積 $S$ $=$ $4 \pi r^2$
※ 球の表面積はその球がちょうど入る円柱の側面積と等しい。球の半径を $r$ とすると、その球がちょうど入る円柱は、底面の円周 $2 \pi r$ 高さ $2r$ である。よってその円柱の表面積は $S’=4 \pi r^2$ となる。このことから、球の体積が $S=S’=4 \pi r^2$ となることが確かめられる
体積:
(1) 角柱・円柱の体積 $V$ $=$ 底面積 $S$ $\times$ 高さ $h$ つまり $V=Sh$
(2) 角錐・円錐の体積 $V$ $=$ $\frac{1}{3}$ $\times$ 底面積 $S$ $\times$ 高さ $h$ つまり $V=\frac{1}{3}Sh$
※ $\frac{1}{3}$ をかけると角錐・円錐の面積が求められる理由:一例として、立方体を対角線によって6等分したものを考えることで、角錐の体積が $V=\frac{1}{3}Sh$ となることを確かめられる。円錐についても、丸暗記ではない理解の仕方をしておくと納得して計算ができる(高校数学の「積分」の知識を使うと計算ができるが、中学数学では「円錐のグラス3杯分が同じ底面積・高さの円柱のグラス1杯分と等しくなる」ことなどを実験で確認しておけば十分に理解が深まる)。
(3) 半径 $r$ の球の体積 $V$ $=$ $\frac{4}{3} \pi r^3$
※ 球の体積は、その球がちょうど入る円柱の体積の $\frac{2}{3}$ である。球の半径を $r$ とすると、その球がちょうど入る円柱は、底面積 $\pi r^2$ 高さ $2r$ である。よってその円柱の体積は $V’=2 \pi r^3$ となる。このことから、球の体積が $V=\frac{2}{3}V’=\frac{4}{3} \pi r^3$ となることが確かめられる(高校数学の「積分」の知識を使うと球の体積の計算式を厳密に証明することも可能)。
中1 > 7章:資料の整理と活用
この章では資料を活用した身近な問題の解決方法を学びます。そのために、資料を整理する方法や、資料の傾向を読み取り判断する方法を正しく理解しましょう。
資料の整理とその活用
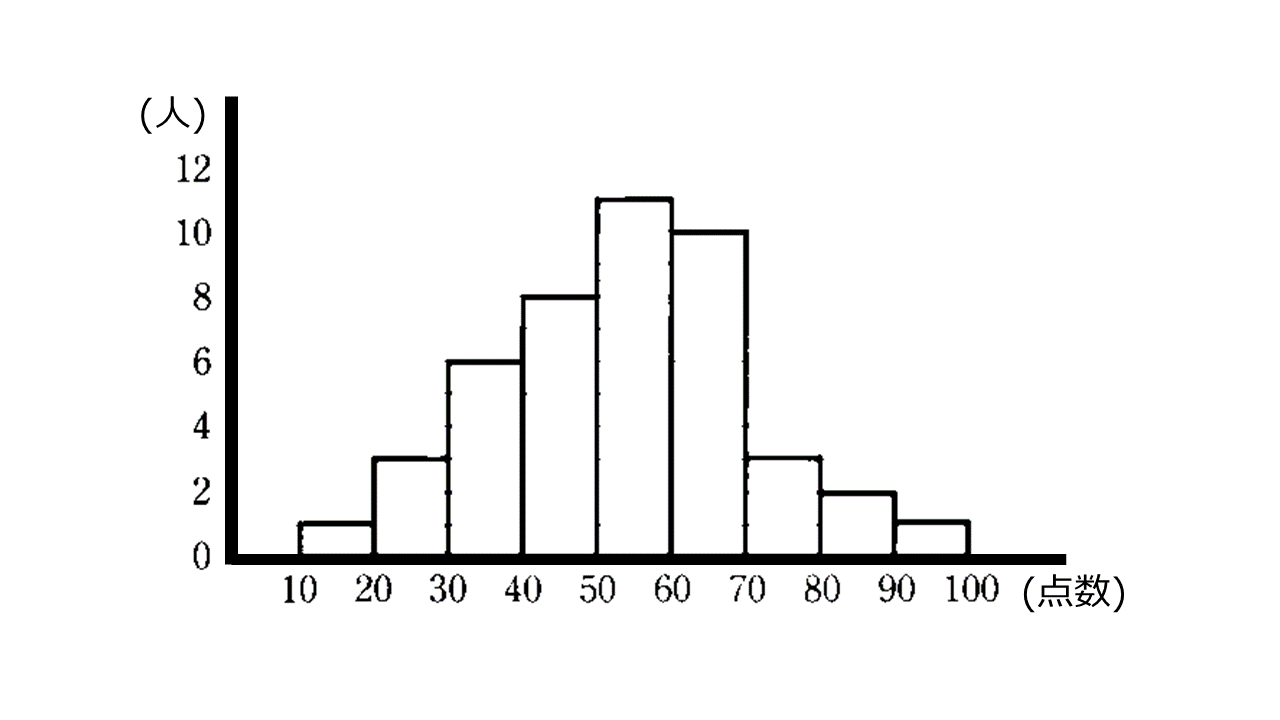
与えられた資料をどのように整理すれば、問題解決につながる特徴や傾向を得ることができるでしょうか。たとえばクラスの生徒のテストの点数の資料が与えられたとします。その資料は、$10$ 点ごとの区間に分けて、その区間に入っている人数を調べてまとめたものでした。このとき、資料を整理するために用いた区間を階級、区間の幅を階級の幅(例えば $60$ 点~ $70$ 点の階級に関してその幅は $10$ 点)、階級の真ん中の値を階級値、それそれの階級に入っている資料の個数をその階級の度数という(例えば $80$ 点~ $90$ 点の階級に $5$ 人の生徒が入っていた場合、度数が $5$ となる)。そして資料をいくつかの階級に分けて階級ごとの度数を示した表を度数分布表、特に度数分布表を柱状のグラフで表したものをヒストグラムという。また全体の度数が異なる資料を比較するときには、そのままでは分布の特徴などを正しく比べることができないので、度数の代わりに、度数の合計に対する割合である相対度数( $\frac{その階級の度数}{度数の合計}$ )という値を用います。相対度数を用いることで、度数の異なる資料に対して正しく分布の特徴などを比較することができます。
資料の特徴を理解したり分かりやすく伝えたりするとき、最大の値から最小の値を引いた値を用いることがあります。最大の値から最小の値を引いた値をその分布の範囲もしくはレンジといいます(範囲 $=$ 最大の値 $-$ 最小の値)。またレンジの他の分布の特徴として、分布から求められる1つの数値である代表値というものがあります。資料を比較するときには、この代表値を比べることが多くあります(主な代表値として平均値・中央値(メジアン)・最頻値(モード)などがあり、目的によって使い分けられます。平均値が多く使用されますが、外れ値(極端な数値)がある場合は中央値や最頻値が用いられることが多くなります)。
資料を正しく読み解くことができるようになると、スポーツやビジネス、医療や研究など、あらゆる場面で活躍できるようになります。本節では上述のような統計の専門用語が多く出てきますが資料の活用(統計)に関する知識は生涯活躍する非常に重要なものなので、着実に身に着けていきましょう。
数学が面白くなる動画―9
数学と物理の力を使えば世界記録をだすこともできるのです。
度数分布表:調査する資料をいくつかの階級に分けて各階級の度数を表にしたもの。
平均値:個々の資料の値の合計を資料の総数で割った値:平均値 $=$ $\{$(階級値$\times$度数)の合計$\}$ $\div$ 度数の合計
中央値(メジアン):資料の値を大きさの順に並べた時の中央の値。資料の総数が偶数の場合は中央にある2つの値の平均値が中央値となる。
最頻値(モード):資料の中で最も多く出てくる値。度数分布表では度数の最も多い階級の階級値。ヒストグラムの最も高い山の部分。
数学が面白くなる動画―10
少子化が進むと将来日本から子供はいなくなるのでしょうか?人口のヒストグラム(人口ピラミッド)を活用して未来予想をしてみましょう。
数学が面白くなる動画―11
1000人中900人が助かる病院Aと800人が助かる病院Bがあるとき、どちらの病院が、いい病院でしょうか?統計データはいつも正しい結果をあたえてくれるのでしょうか?
近似値と有効数字
$1$ と $1.00$ とでは何か違いがあるのでしょうか。例えば地球の大きさは半径「約 $6378$ km」で太陽からの距離は「約 $149600000$ km」です。$6378$ kmという数字には全て意味がありそうですが、$149600000$ kmという数字は、どこまで正確に測定された距離なのでしょうか。ここで有効数字という考え方を導入すると、地球と太陽の距離は有効数字を $4$ 桁と仮定すると $1496 \times 10^5$ kmと表すことができ、見やすく、そして数字の意味も分かりやすくなります。本節では、このような数字の表示の決まりや意味について理解しましょう。
近似値:真の値ではないが、それに近い数。例えば四捨五入した数など。はかりやものさしなどの計器では、最小の目もりの $\frac{1}{10}$ を目分量で読み取り四捨五入した値を用いることが多いが、これも近似値であると考えることができる。
誤差:誤差 $=$ 近似値 $-$ 真の値
例
四捨五入すると $10$ になったある数 $a$ は $9.5≦a<10.5$ の範囲にある。従って、この場合の誤差の絶対値はどんなに大きくても $0.5$ であることがいえる(誤差 $=$ 10 $-$ 真の値($9.5~10.5$) のため)。
有効数字:測定によって得られた数字のうちで信頼できる数字。
例
$100$ g単位の計量器で計測した時 $2400$ gだと分かった時の有効数字は $2$ と $4$ の $2$ 桁となる(千の位の $2$ と百の位の $4$ は測定された意味のある数として信頼できる「有効な数」であるが、十の位と一の位の $0$ は単に位を示しているだけで、$0$ と計測されたわけではなく信頼できない)。どこまでが有効数字かを明確に示すためには $2.4 \times 10^3$ gのように、(整数部分が1桁の数) $\times$ ($10$の累乗)の形で表記すると分かりやすい。


