🔄 最終更新日 2019年1月26日 by takara_semi
数学でタイムトラベル
数学の一つの利用方法として「未来の予測」があります。気象予測や新設計の自動車や飛行機などの性能の予測、人の行動予測など、例を挙げればきりがありません。未来を計算するということは、完全に実世界の現象と一致することは困難ですが、限定的な環境での未来を垣間見ることができるということになります。言い換えれば、数学によってタイムトラベルのような経験をすることができるのです。今回は「ロボットの配置シミュレーション」と「波のシミュレーション」および「未来を予測できないカオスな現象」の3つを例に、数学で未来を覗いてみましょう。
ロボットの配置シミュレーション
一つ目の例はロボットの行動シミュレーションです。この例では、複数の移動ロボットが障害物のある環境の中で、互いが「見える」位置に自動的に移動する配置問題(The Sensor Deployment Problem)を考えます。ここでいう「見える」とは、2つのロボットを直線で結んだときに、その間に障害物が存在しない状態を意味します。この問題を定式化すると以下のようになります。
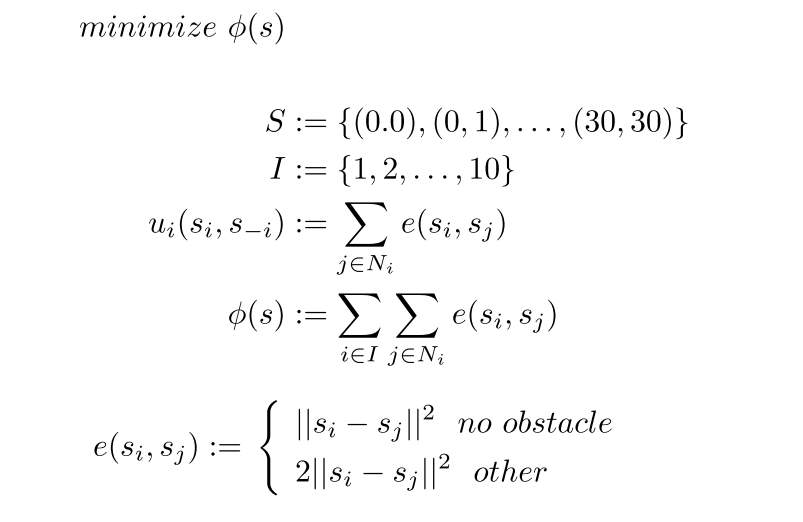
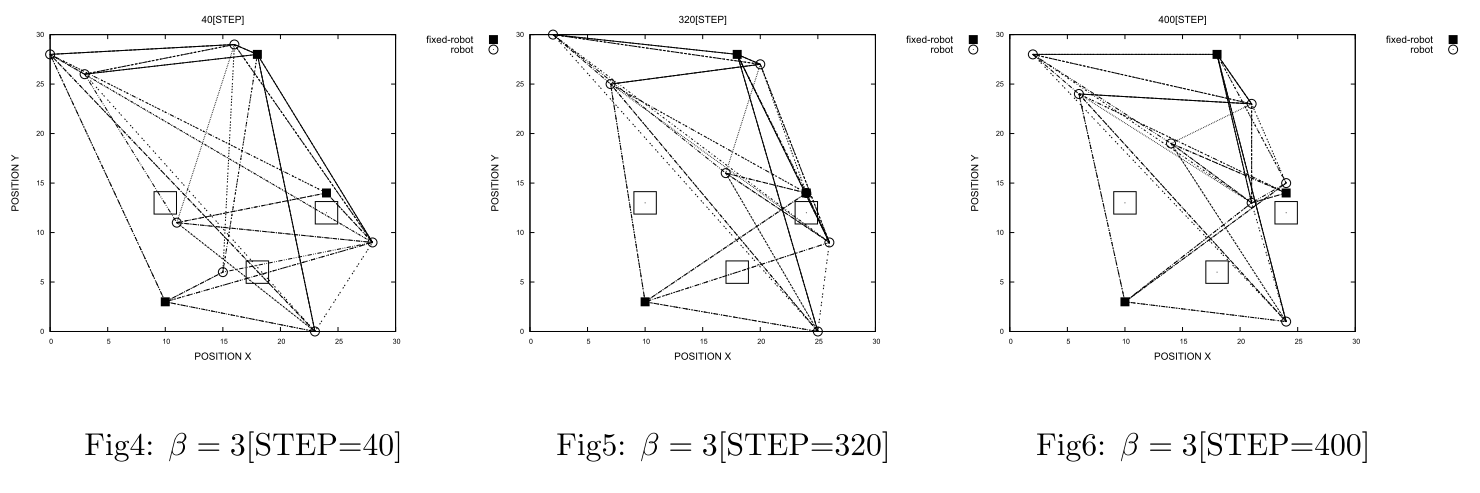
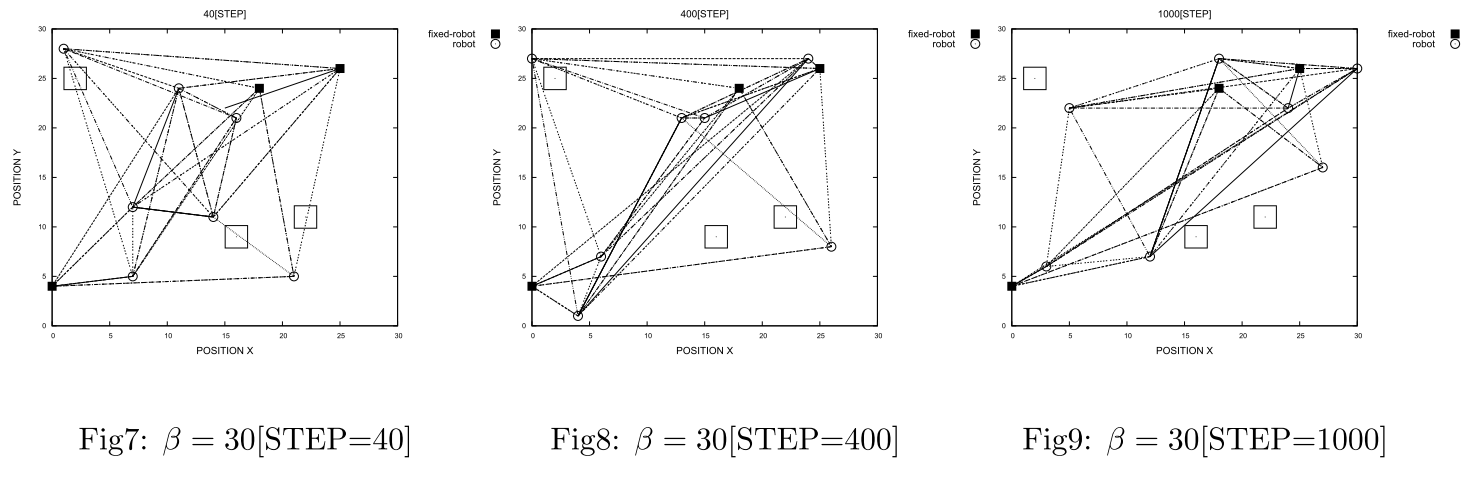
$\small{u}$は効用関数、$\small{e}$は損失関数(コスト関数)です。簡単に説明すると、障害物が2つのロボットの間に存在する場合はコストが高くなるよう定式化しており、目的関数$\small{\phi(s)}$が最小化されるように問題を解くことで、効率的にロボットを配置できます。初期状態(配置、センサー接続関係)は各シミュレーションごとにランダムに設定します。またFig1~Fig9中の白い四角の印は障害物(obstacle)を表しています。The Sensor Deployment Problemを$\small{\beta=0}$で実行した結果をFig.1~Fig.3に、$\small{\beta=3}$で実行した結果をFig.4~Fig.6に、$\small{\beta=30}$で実行した結果をFig.7~Fig.9に示します。それぞれの結果について見ていきましょう。The Sensor Deployment Problemによってロボット(状態$\small{s_i(t)}$)が移動可能な近傍状態$\small{\hat{s}}$に移動する確率を$\small{P_r[s_i(t+1)=\hat{s}]}$と定義すると、
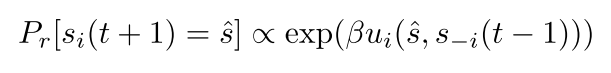
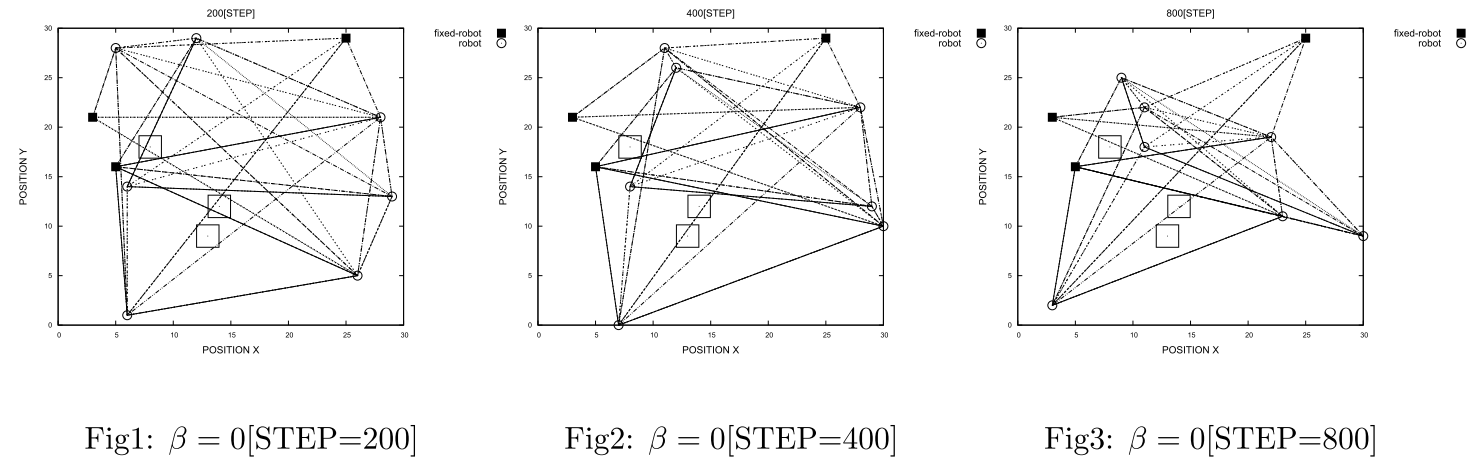
という関係が成り立ちます。この関係式をもとに$\small{\beta}$の変化によるロボットの配置ネットワークの挙動の変化を考えると、$\small{\beta=0}$の場合の振る舞いは、上式から明らかな通りランダムに動き、ロボット間のネットワーク構造が障害物を避けるように変化する振る舞いは示しません。$\small{\beta}$が小さい($\small{\beta}$=3.0)場合の振る舞いは、上式の指数関数の形が裾の広い形状となり、各ネットワーク間のリンクの距離が極端にならず、ある程度一定となるようにロボットの位置が変化するような振る舞いが見られました。また$\small{\beta}$が大きい($\small{\beta}$=30.0)場合の振る舞いは、上式の指数関数の形が裾の狭い形状となり、ネットワークのリンクの長さが多少極端になってしまうものの、近傍のロボットが集まり、いくつかのクラスタを形成するような振る舞いを示しました。
いずれの場合でも$\small{\beta}$が0でない限り、障害物を避けるようにロボットの配置ネットワークを形成することが確かめられ、最適化問題を解くことにより、障害物が存在する部屋においてロボットが互い見えるように上手く移動するようなシミュレーション結果を得ることができた。このようなロボットの移動計画問題も、一種の未来予測と言えるでしょう(人の行動予測など、より直接的な「未来予測」の問題が、ロボティクスや人工知能の分野には多数存在します。興味がある場合は、専門書を読むことをお勧めします)。
波のシミュレーション1(Burgers方程式)
次の例は、波の形状のシミュレーションです。流体の振舞いを記述する有効な方程式としてナビエ-ストークス方程式というものがあるのですが、今回はこの式を一次元で考えた場合の、圧力の影響を無視できる場合に相当するBurgers方程式を利用して、波という物理現象の数値解析を行います(数値解析・数値計算とは、数式を解析的に解くのではなく、コンピュータを利用して、代わりに近似的な解を得る方法です)。Burgers方程式は以下のように表されます。
\begin{equation}
\frac{\partial f}{\partial t}+f\frac{\partial f}{\partial x}=\beta\frac{\partial^2 f}{\partial x^2}
\end{equation}
この方程式に関しての初期値問題を考えます。今回は初期条件(初めの波の状態)を:$\small{f(x,t=0)=\exp(-x^2)}$$\small{(-\infty < x < \infty)}$とします。まずは$\small{\beta}$=0の場合の解(波の挙動)を求めます。
\begin{equation}
\frac{\partial f}{\partial t}+f\frac{\partial f}{\partial x}=\beta\frac{\partial^2 f}{\partial x^2}\nonumber
\end{equation}
上式の非線形移流項に中心差分を適用すると
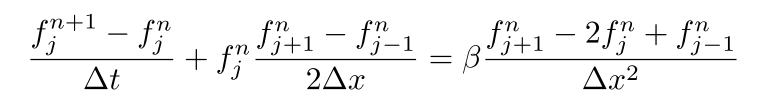
となります。だたし、変数$\small{f}$の下付きの添字は位置、上付きの添字は時刻を表しています。これにより$\small{\nu=\beta\frac{\Delta t}{\Delta x^2}}$として、次式を得ることができます。
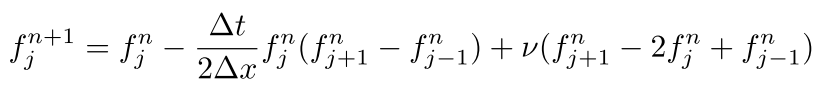
この差分方程式を数値計算した結果をFig1~Fig3に示します。Burgers方程式の移流項は、波高$\small{f}$が大きいほど速い速度で右方向に移動するもので、波の突き立ちが生じ、衝撃波に似た急峻な不連続面を形成する様子が見て取れます。
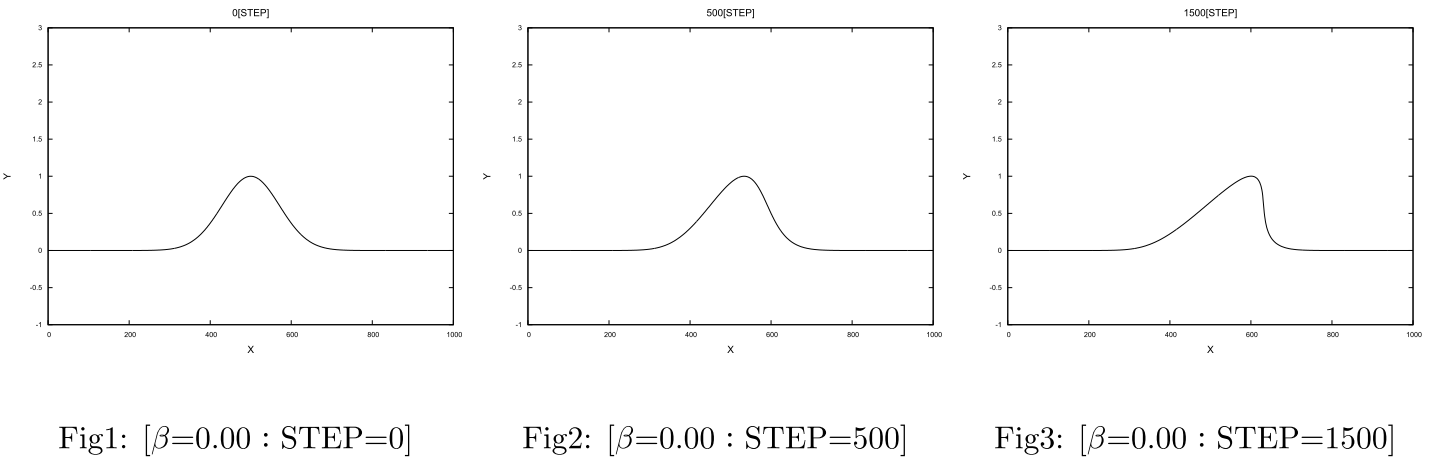
続いて$\small{\beta}$=0.01の場合の解(波の挙動)を同様の手順で計算します。その結果得られた$\small{\beta=0.01}$の場合の数値計算結果をFig4~Fig6に示します。
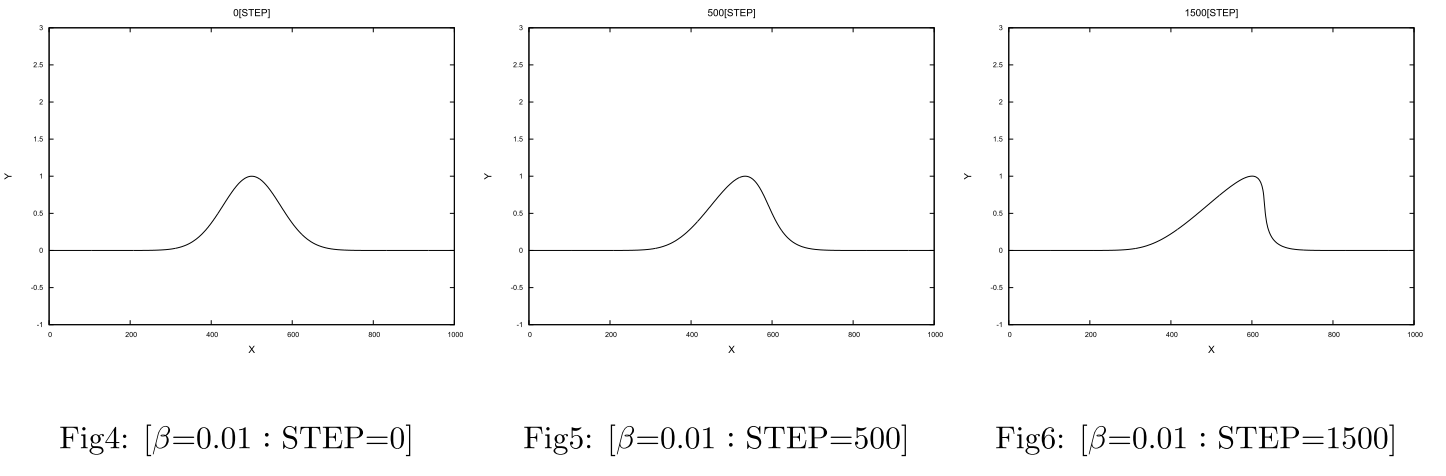
図をみると$\small{\beta=0.01}$の場合と$\small{\beta=0}$の場合でほとんど変わらない結果が得られましたが、これは$\small{\beta=0}$の数値解析においても、風上法における空間に対する微分として
\begin{equation}
\frac{\partial u}{\partial x}\simeq \frac{u_j^n-u_{j-1}^n}{\Delta x}
\end{equation}
と近似した影響だと考えられます。これは
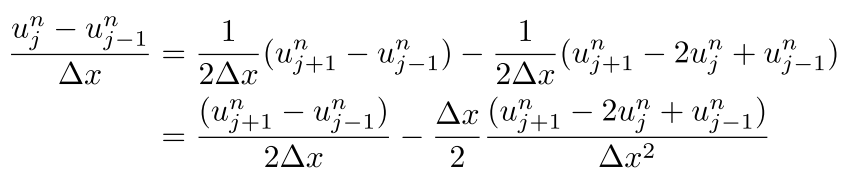
と等価であり、第2項にあるように、もともとの方程式にはなかった2階微分($\small{\frac{\partial^2 u}{\partial x^2}}$)の拡散の性質が暗に含まれていたため、$\small{\beta}$の有無による結果の差異が顕在化されなかったのではないと考えられます。Burgers方程式のような偏微分方程式を解くことは、物理現象の未来予測と密接に関連しており、数理科学を代表する学問の一つでもあります。微分方程式を解くことで、現象の未来を覗くことができるのです。
波のシミュレーション2(KdV方程式)
KdV方程式は、Burgers方程式と同様、非線形波動を記述する非線形偏微分方程式の一つで、例えば以下のような数式として表されます(以下では係数に既に具体的な定数が代入されています)。
\begin{equation}
\frac{\partial u}{\partial t}-6u\frac{\partial u}{\partial x}+\frac{\partial^3 u}{\partial x^3}=0
\end{equation}
まず上式について$\small{u(x,0)=-6{\rm sech}^2x}$という初期条件(初めの波の形)のもとで数値計算を行います。
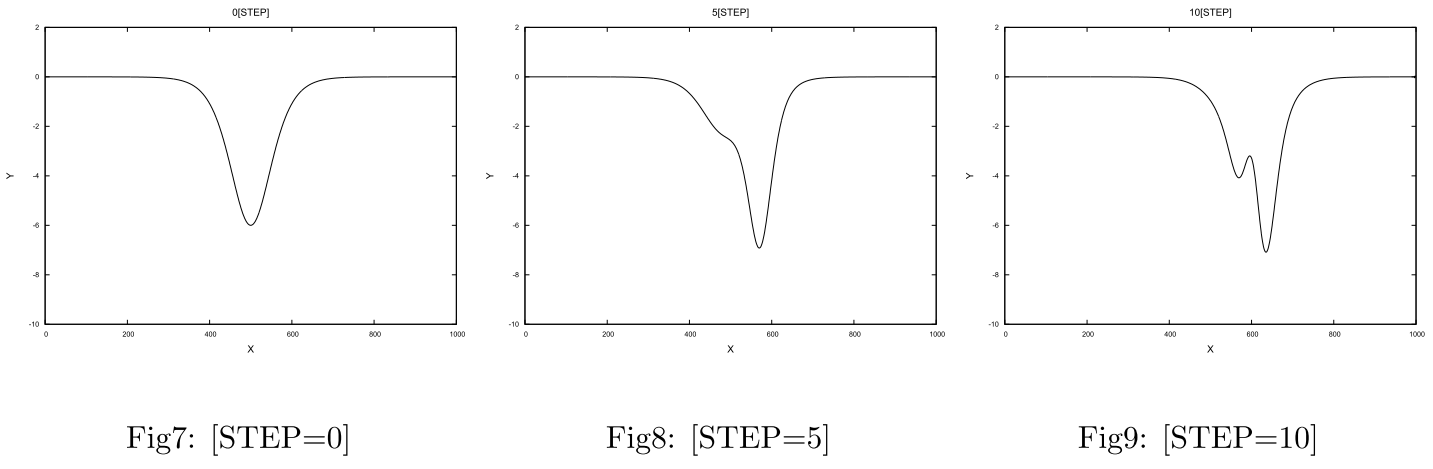
KdV方程式は今回与えられた条件下においては2-ソリトン解になります。ソリトンとは掻い摘んで説明すると、非線形方程式に従う孤立波のことを意味します。数値計算には2次の保存量までを考慮したスキーム
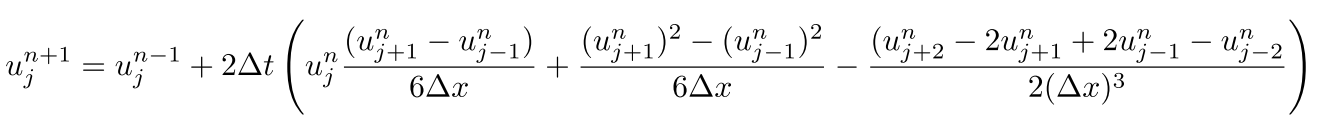
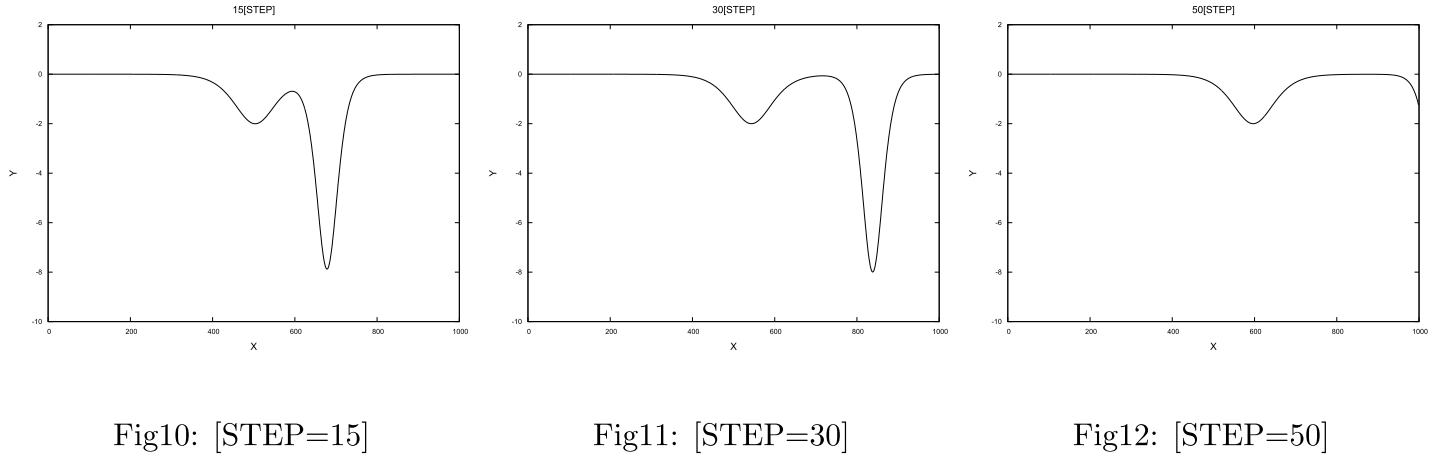
を用います。ただし、変数$\small{u}$の下付きの添字は位置、上付きの添字は時刻を表しています。数値解析の結果をFig7~Fig12に示します。図から見て取れるようにKdV方程式は与えられた条件下において2-ソリトン解(2つの孤立波の形状)となることが確かめられます。続いて、与えられたKdV方程式の厳密解(数式を解析的に解いた結果)
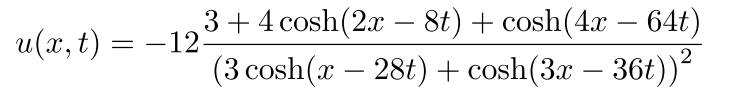
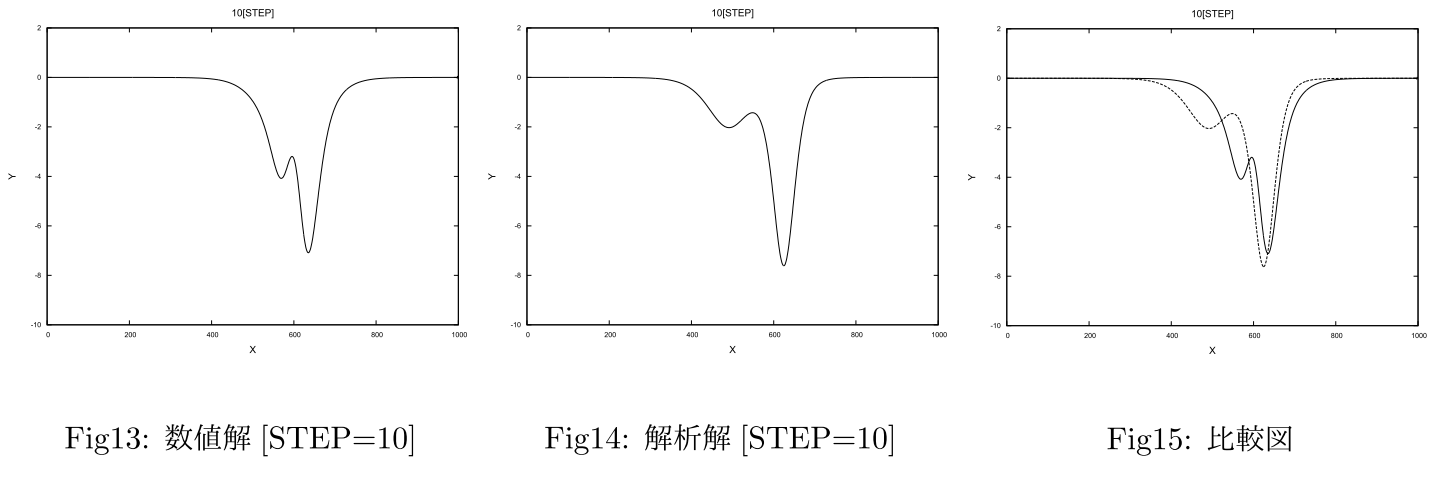
と数値解析の結果を比較してみます。計算ステップ10(STEP=10)における厳密解
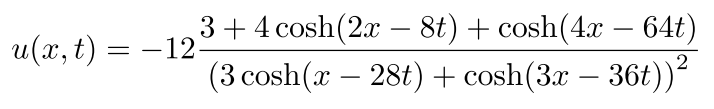
の結果をFig14に、数値解の結果をFig13、それぞれを重ね合わせた結果をFig15に示します。数値解と解析解を比較すると、数値解は時間が進むにつれて減衰している様子が見て取れます。この減衰の原因は、離散化のために用いた差分式に起因していると考えられます。用いた差分式は時間について前進差分を行ったため、誤差の原因となる減衰が生じたのではないかと考えられます。また、数値計算の場合はどうしても計算誤差が時間の経過に伴い蓄積してしまうため、解析解との差異は必然的に生じるものであるとも考えられます。誤差の軽減のためには、より高次の近似を行うことが有効だと考えらます。このように、コンピュータを用いた数値計算によるシミュレーションで現象を完全に再現することは、コンピュータの性能や計算コストなどの観点から困難な場合が多いことを念頭に置いて、計算結果を見ていく必要があります。
未来を予測できない現象(Lorenz方程式)
これまでは、ある程度の未来を予測できる例を見てきましたが、ここでは「未来を予測できない現象」について考えます。全ての現象を数学を用いて予測することができるわけではないのです。このような数的な誤差によって予測できないとされている複雑な様子を示す現象を「カオス」と呼び、このような現象を扱う学問をカオス理論と言います。カオス的な振舞いを示す非線型方程式の一つとしてLorenz方程式があります。これは大気変動モデルを研究していた気象学者ローレンツが論文”Deterministic Nonperiodic Flow”(1963) の中で提示された数理モデルで、以下のように表されます。
\begin{eqnarray}
\frac{dx}{dt}&=&\sigma(y-x)\nonumber\\
\frac{dy}{dt}&=&-xz+rx-y\nonumber\\
\frac{dz}{dt}&=&xy-bz\nonumber
\end{eqnarray}
この方程式に関して$\small{b=\frac{8}{3}, \sigma=10, r}$:(パラメータ)のときについて考えます。まず、上式の平衡点を求めその安定性について見ていきます。上式に関して右辺=0の場合を考えると、それぞれ以下のような関係が成り立ちます。
\begin{eqnarray}
\sigma(y-x)&=&0\nonumber\\
-xz+rx-y&=&0\nonumber\\
xy-bz&=&0\nonumber
\end{eqnarray}
$\small{x}$についての方程式を得るように連立方程式を解くと、次式が得られます。
\begin{eqnarray}
x^3-b(r-1)x&=&0
\end{eqnarray}
得られた3次方程式を解くと
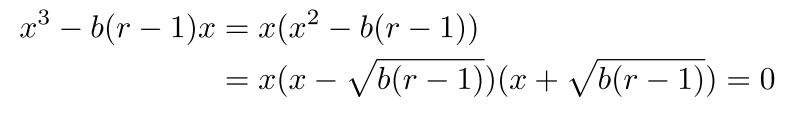
となり、平衡点$\small{x=0,\pm \sqrt{b(r-1)}}$が得られます。また、与えられた連立方程式から$\small{y=x,z=\frac{x^2}{b}}$であるから

の3つの平衡点が得られます。Lorenz方程式の解の挙動を調べると、$\small{\sigma,b,r}$の値により、解の挙動が全く異なることが分かります。定点に収束する場合や、周期軌道を描く場合がある一方、$\small{\sigma>b+1}$で$\small{r>\frac{\sigma(\sigma+b+3)}{\sigma-b-1}=24.74}$の場合は不安定になり、アトラクタと呼ばれる2種の領域を8の字状に周回し続け、定点に収束したり、周期軌道をたどることもなく、未来の状態が予測できない軌道を描きます。このような予測不可能な状態をカオスと呼びます。つまり、安定解析を行った結果をまとめると
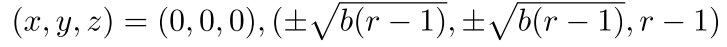
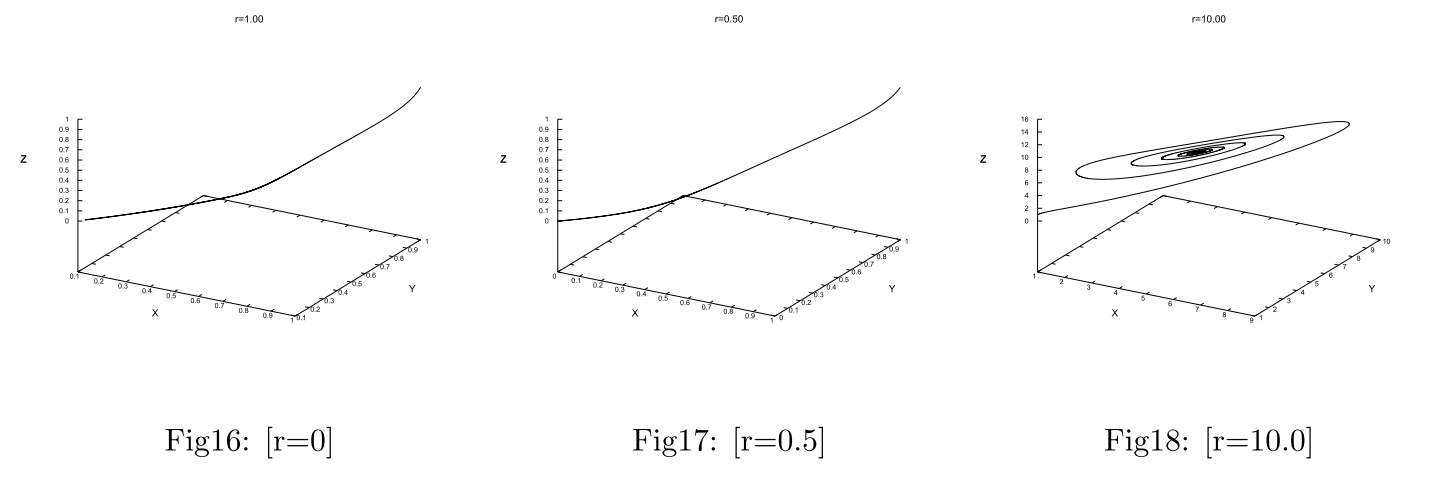
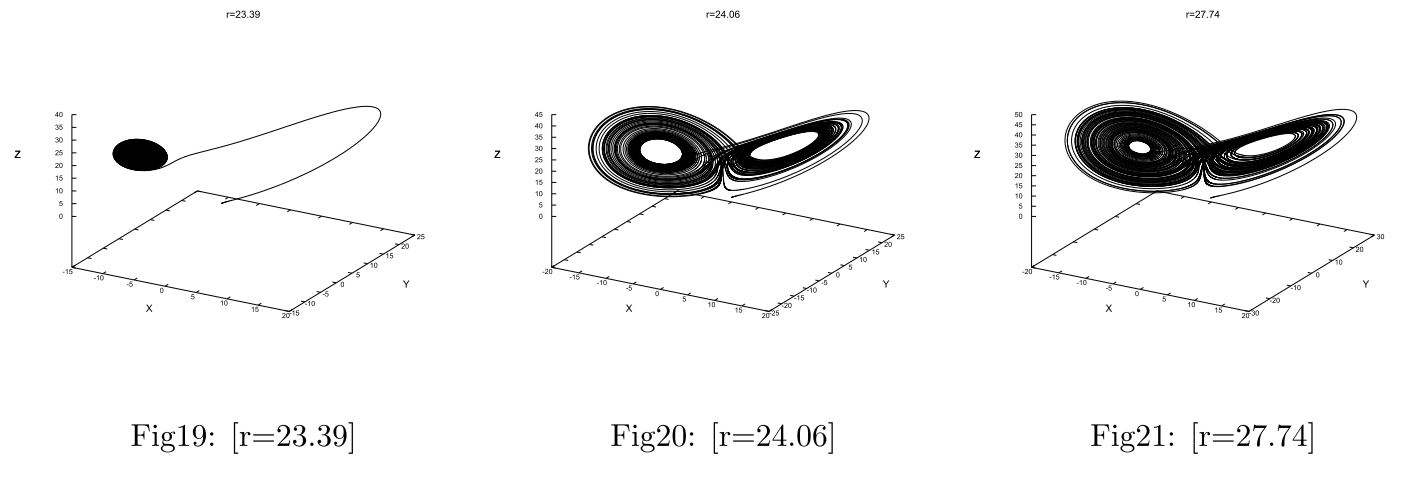
という結果がいえます。続いて$\small{r}$の値を変えたときの$\small{(x,y,z)}$空間内の軌道を図示します。Lorenz方程式の初期値問題の解法としてはRunge-Kutta法を用い、精度の高い近似による数値計算を行いました。$\small{r}$の値としては、次の6つのパラメータを選びました。それぞれの場合の結果をFig16~Fig21および以下に示します。

Fig16~Fig21の結果は、初めに検討した安定性の議論の結果と一致していることが分かります。またFig20,Fig21においては、アトラクタと呼ばれる2種の領域を8の字状に周回する様子も確認することができ、定点に収束したり、周期軌道をたどることのない、カオスの状態であることが分かります。
最後に、Lorenz方程式の初期値をわずかに変化させた時の、2つの軌道の挙動を見てみます。2つの初期値は次のように設定します。

数値計算の結果得られた$\small{x}$座標値の結果を比較したものをFig22に示します。Fig22をみると、はじめは微小な初期値の差異による軌道の変化は見られませんが、15000[STEP]を超えたあたりから徐々に差が見られるようになり、その差は急激に増していき、カオス的な振る舞いを示すことが確かめられます。高度に発達した数学とコンピュータの力を利用しても予測できない現象があるというのは、何とも神秘的で、魅力的なことだと思います。どのような現象でも予測できてしまう世界だときっと面白くないでしょうから。