🔄 最終更新日 2024年1月22日 by takara_semi
$\triangle \mathrm{ABC}$ において $\mathrm{AB}=\mathrm{AC}=6$, $\cos \angle \mathrm{BAC}=\frac{1}{3}$ である.
(1) $\mathrm{BC}=(ア)\sqrt{(イ)}$
であり, $\triangle \mathrm{ABC}$ の面稘は $(ウ)(エ)\sqrt{(オ)}$である.また,$\triangle \mathrm{ABC}$ の外接円の半径は $\frac{(カ)\sqrt{(キ)}}{(ク)}$ である.
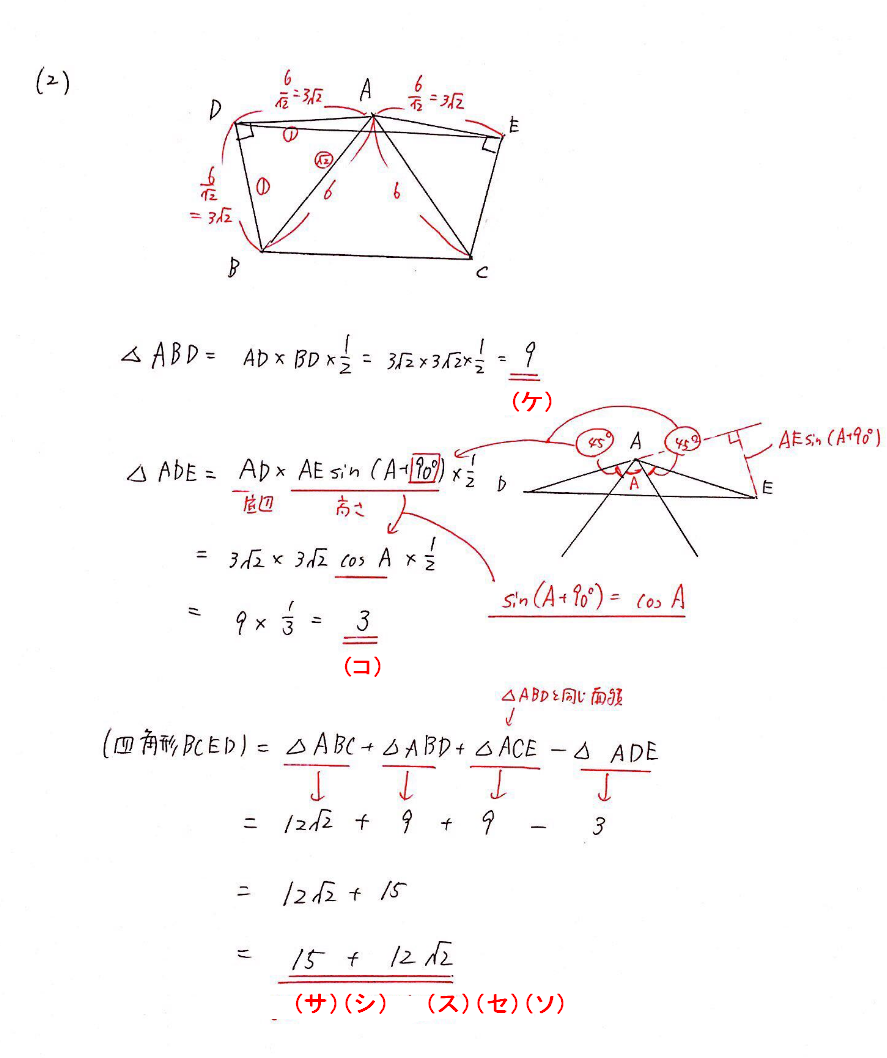
(2) $\triangle \mathrm{ABC}$ の外側に辺 $\mathrm{AB}, \mathrm{AC}$ を斜辺とする直角二等辺三角形 $\mathrm{ABD}, \mathrm{ACE}$ をつくるとき,$\triangle \mathrm{ABD}$ の面積が(ケ), $\triangle \mathrm{ADE}$ の面積が(コ)であるから四角形 $\mathrm{BCED}$ の面積は $(サ)(シ)+(ス)(セ)\sqrt{(ソ)}$ である.

問題文を図示することで,正弦定理,余弦定理での計算ミスを減らすことができます.
検索キーワード:
余弦定理, 正弦定理, $\triangle \mathrm{ABC}$, $\mathrm{AB}=\mathrm{AC}=6$, $\cos \angle \mathrm{BAC}=\frac{1}{3}$, $\mathrm{BC}$, $\triangle \mathrm{ABC}$ の面稘, $\triangle \mathrm{ABC}$ の外接円の半径, $\triangle \mathrm{ABC}$ の外側, 辺 $\mathrm{AB}$, $\mathrm{AC}$ を斜辺とする直角二等辺三角形 $\mathrm{ABD}$, $\mathrm{ACE}$, $\triangle \mathrm{ABD}$ の面積, $\triangle \mathrm{ADE}$ の面積, 四角形 $\mathrm{BCED}$ の面積.