🔄 最終更新日 2019年12月11日 by takara_semi
中3 > 5章:相似
本章では、形が同じ図形の性質・相似の性質について学び、身の回りでその性質を利用している例をみつけてみましょう。例えば、キッチンにあるスパゲッティメジャーでは面積比の相似比の関係を利用して1人分や2人分を計測しており、調理用スプーンでは体積比と相似比の関係を利用して分量を計量できるように設計されています。このような例の他にも、直接測ることが難しい「地形や建造物の計測・縮図の作成」などにも相似が利用されています。本章の知識を身に付け、相似の性質をより身近なものとして活用できるようになりましょう。
相似な図形
本節では、形を変えずに拡大縮小して得られる図形の性質についてみていきましょう。1つの図形を、形を変えずに一定の割合に拡大縮小して得られる図形は、もとの図形と相似であるといいます。下の図で、四角形(ア)と四角形(イ)は相似です。また四角形(ウ)は四角形(イ)を左右反転した図形であり、2年で学んだ通り、この2つの四角形は合同です。このような場合にも、四角形(ア)と四角形(ウ)は相似であるといいます。四角形 $ {\rm ABCD}$ と四角形 ${\rm A’B’C’D’}$ が相似であることを四角形 $ {\rm ABCD}∽{\rm A’B’C’D’}$ と表します。多角形の相似を記号 $∽$ を用いて表す場合、合同の時と同じように、対応する頂点を周に沿って同じ順に書きます。相似な図形では、対応する部分の長さの比は全て等しく、対応する角の大きさはそれぞれ等しくなります。また、下の図の四角形(ア)と四角形(イ)のように、2つの図形の対応する点どうしを通る直線が全て1つの点 ${\rm O}$ に集まり、点 ${\rm O}$ から対応する点までの距離の比が全て等しいとき、それらの図形は、点 ${\rm O}$ を相似の中心として相似の位置にあるといいます。つまり相似の位置にある2つの図形は相似です。
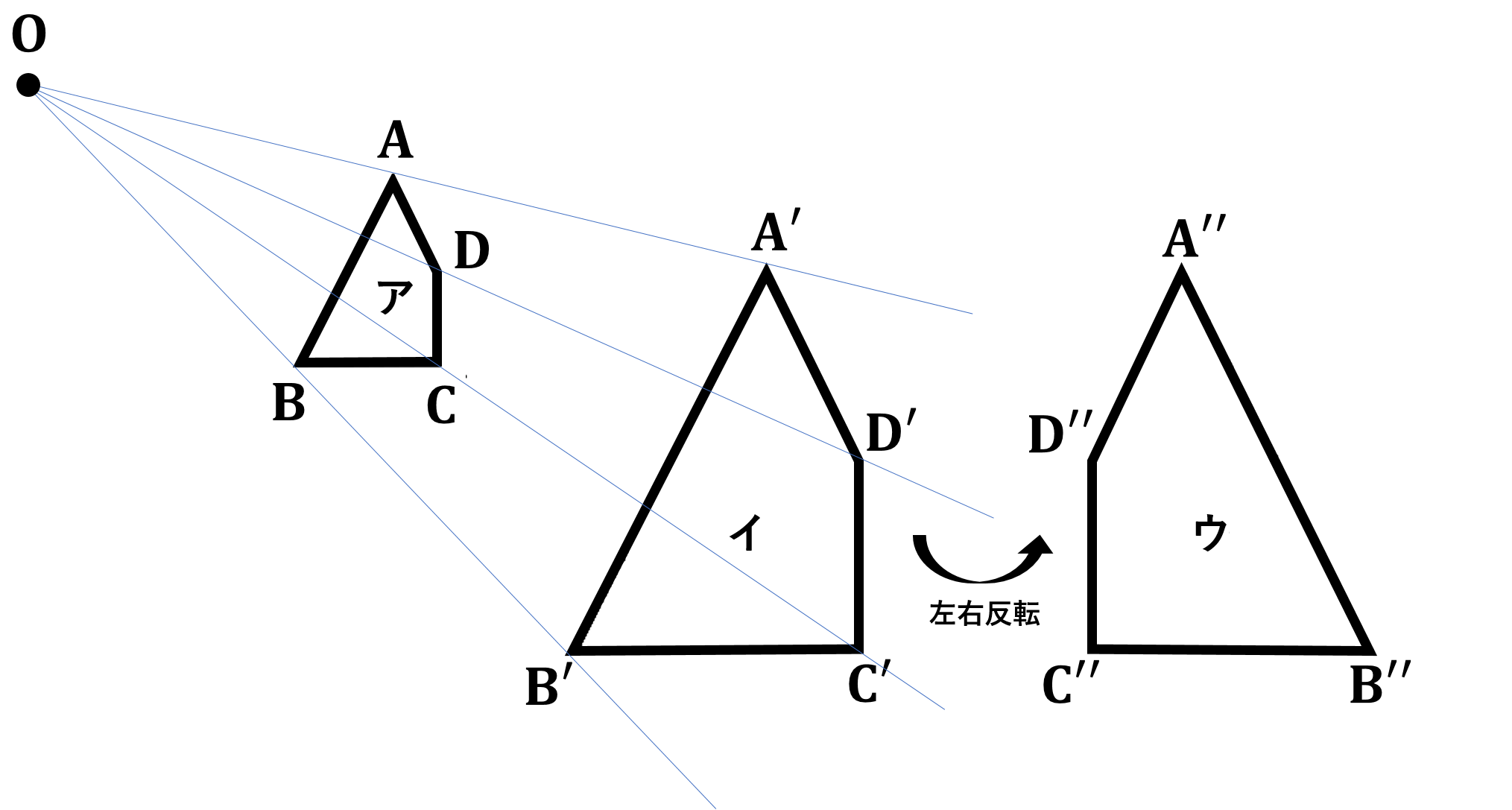
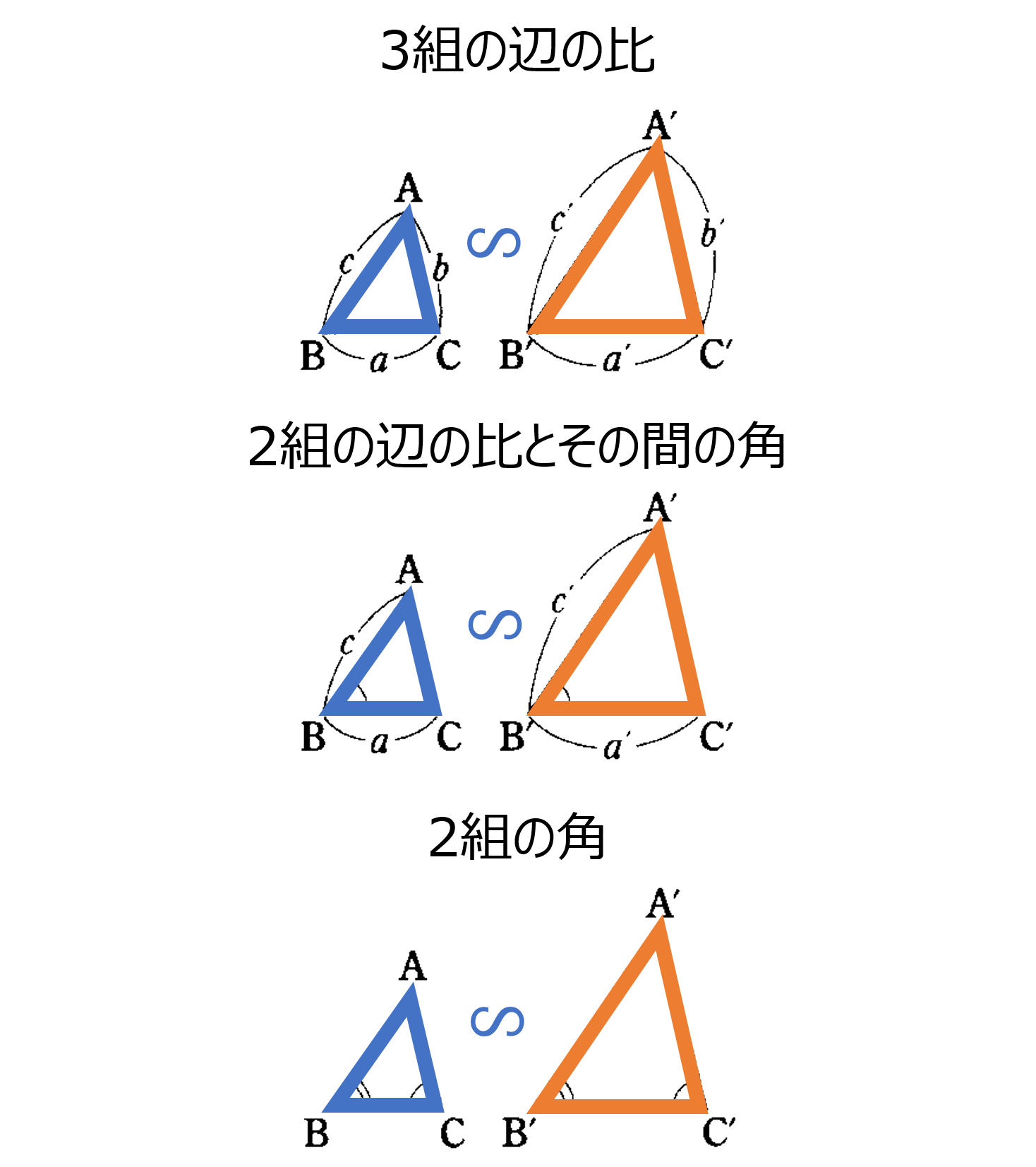
相似な図形で対応する部分の長さの比を相似比といいます。例えば、相似な2つの円では、その相似比は半径の比と等しくなります。続いて三角形の相似条件についてですが、2つの三角形において (1) 3組の辺の比が全て等しい (2) 2組の辺の比とその間の角がそれぞれ等しい (3) 2組の角がそれぞれ等しい のいずれかが成り立つときに相似であるといえます。この相似条件は、2年で学んだ合同条件と比較しながらみてみると、理解や暗記がしやすくなります。
次に三角形と比の定理についてみていきます。下の図の ${\rm \triangle{ABC}}$ の辺 ${\rm AB,AC}$ 上の点をそれぞれ ${\rm D,E}$ とするとき (1) ${\rm DE}/ \! \! /{\rm BC}$ ならば ${\rm AD:AB=AE:AC=DE:BC}$ (2) ${\rm DE}/ \! \! /{\rm BC}$ ならば ${\rm AD:DB=AE:EC}$ が成り立ちます。
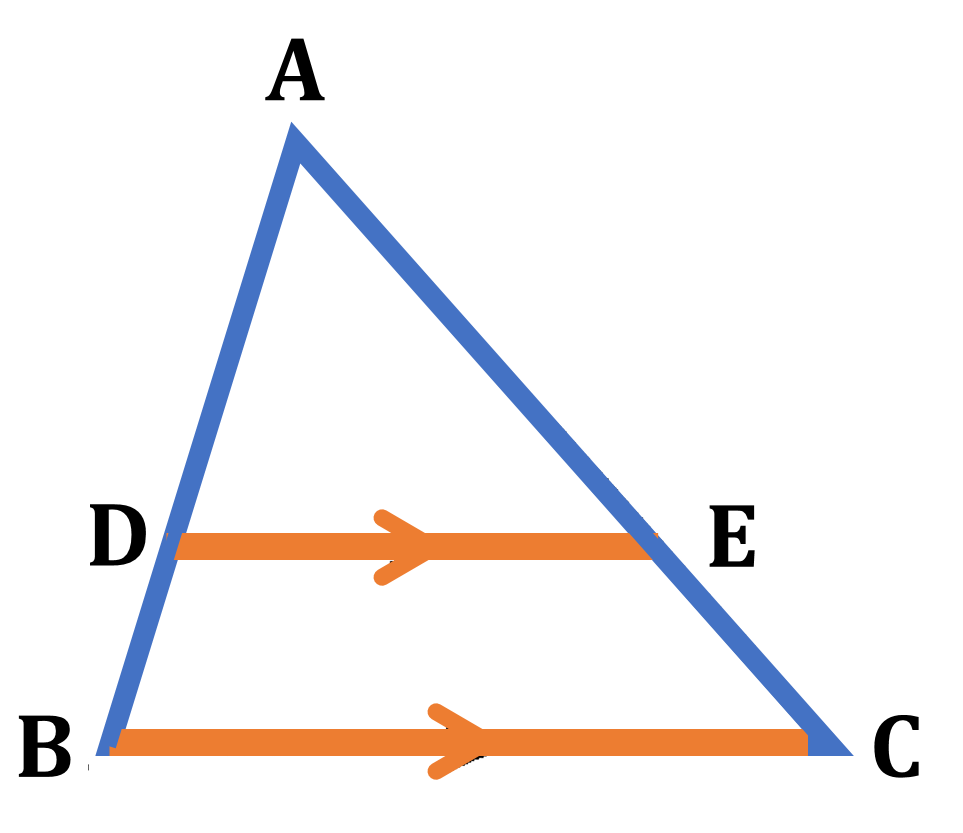
最後に、三角形の比の定理の逆が成り立つかどうかを考えてみましょう。下の図の ${\rm \triangle{ABC}}$ において、辺 ${\rm AB,AC}$ 上に ${\rm AD:AB=AE:AC}$ となるように点 ${\rm D,E}$ をとると ${\rm DE}/ \! \! /{\rm BC}$ となることを証明できれば、三角形の比の定理(1)の逆が成り立つといえます。
${\rm \triangle{ADE}}$ と ${\rm \triangle{ABC}}$ において
仮定から ${\rm AD:AB=AE:AC}$・・・①
また ${\rm \angle A}$ は共通・・・②
①②より、2組の辺の比とその間の角がそれぞれ等しいから
${\rm \triangle{ADE}} ∽ {\rm \triangle{ABC}}$
したがって
${\rm \angle ADE} ∽ {\rm \angle ABC}$
同位角が等しいから
${\rm DE}/ \! \! /{\rm BC}$
よって三角形の比の定理の逆が成り立つことが確かめられました。
定理(2)の逆の証明は割愛しますが、各自で確認しておきましょう。よって、まとめると三角形と比の定理の逆は次のようになります。${\rm \triangle{ABC}}$ の辺 ${\rm AB,AC}$ 上の点をそれぞれ ${\rm D,E}$ とするとき (1) ${\rm AD:AB=AE:AC}$ ならば ${\rm DE}/ \! \! /{\rm BC}$ (2) ${\rm AD:DB=AE:EC}$ ならば ${\rm DE}/ \! \! /{\rm BC}$ が成り立ちます。
相似:2つの図形の一方を拡大または縮小した図形が他方と合同になるとき $\to$ 2つの図形は相似である。
(1) 対応する線分の長さの比はすべて等しい。
(2) 対応する角の大きさはそれぞれ等しい。
三角形の相似条件:2つの三角形において:
(1) 3組の辺の比がすべて等しい。$a:a′=b:b′=c:c′$
(2) 2組の辺の比とその間の角がそれぞれ等しい。$a:a′=c:c′,\angle {\rm B}=\angle {\rm B}′$
(3) 2組の角がそれぞれ等しい。$\angle {\rm B}=\angle {\rm B}′, \angle {\rm C}=\angle {\rm C}′$
平行線と線分の比
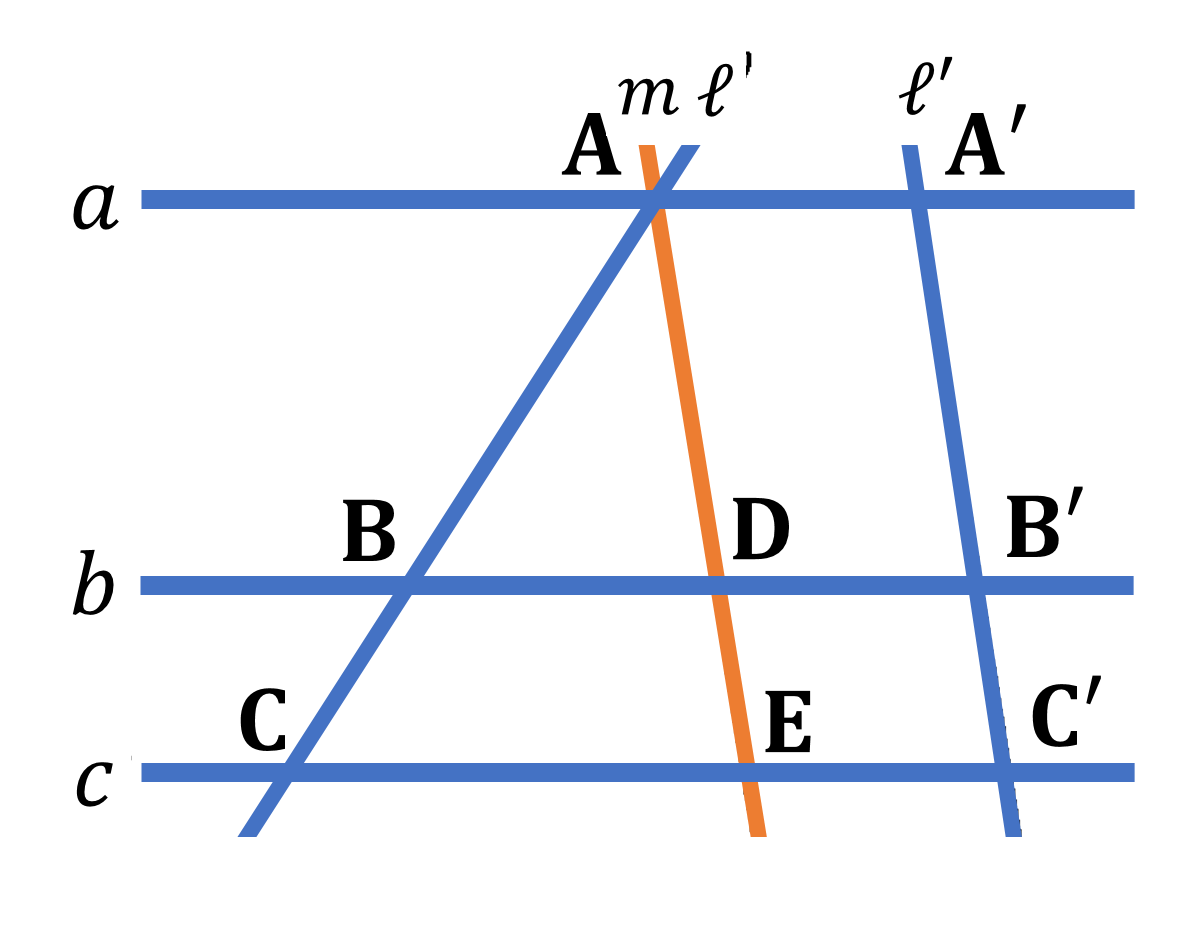
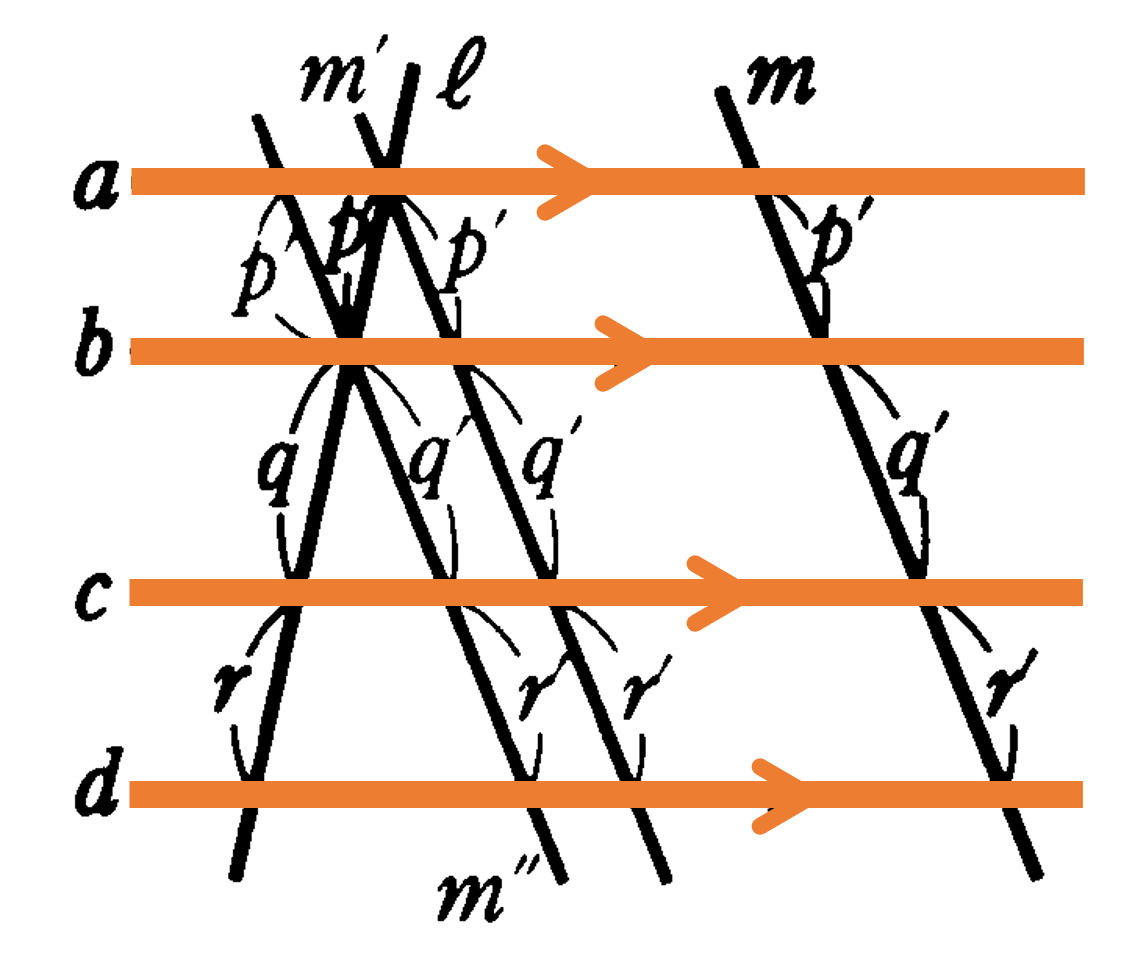
本節では、平行線と比についてみていきましょう。三角形と比の定理から新しい性質を導いていきます。直線が平行線と交わるとき、一般に次の定理が成り立ちます。下の図のように、平行な3つの直線 $a,b,c$ が直線 $\ell$ とそれぞれ ${\rm A,B,C}$ で交わり、直線 $\ell’$ とそれぞれ ${\rm A’,B’,C’}$ で交われば ${\rm AB:BC=A’B’:B’C’}$ が成り立ちます。この定理は以下のように証明できます。
点 ${\rm A}$ を通り $\ell’$ に平行な直線 $m$ をひき、$b,c$ との交点をそれぞれ ${\rm D,E}$ とします。${\rm \triangle{ACE}}$において ${\rm BD}/ \! \! /{\rm CE}$ であるから
${\rm AB:BC=AD:DE}$・・・①
また四角形 ${\rm ADB’A’}$ と四角形 ${\rm DEC’B’}$ はともに平行四辺形であるから
${\rm AD=A’B’, DE=B’C’}$・・・②
①②より
${\rm AB:BC=A’B’:B’C’}$
がいえます。
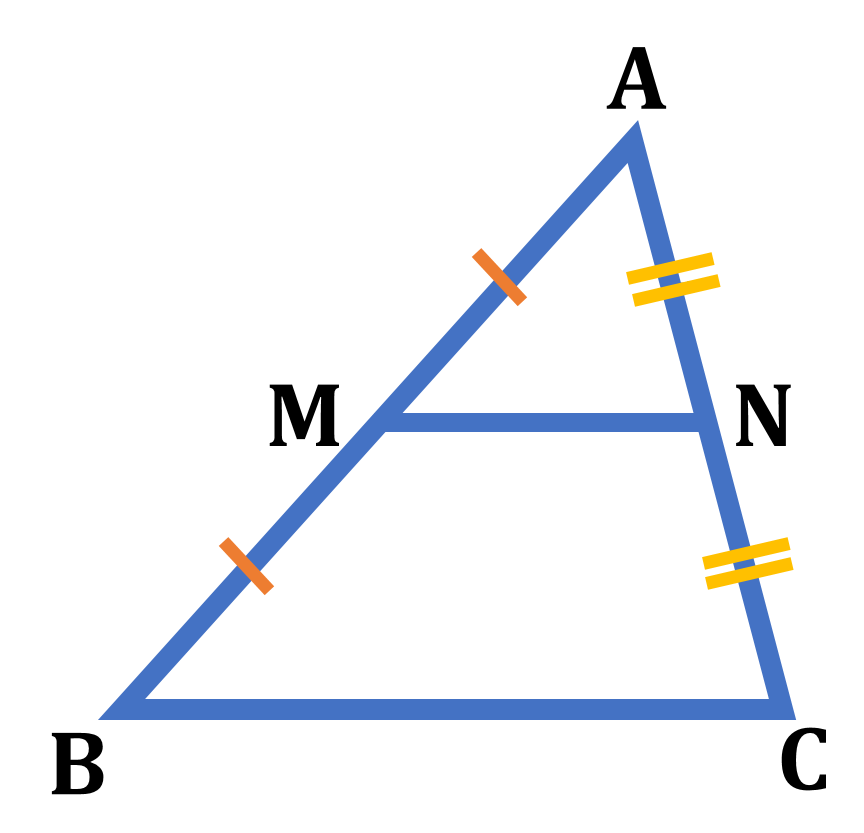
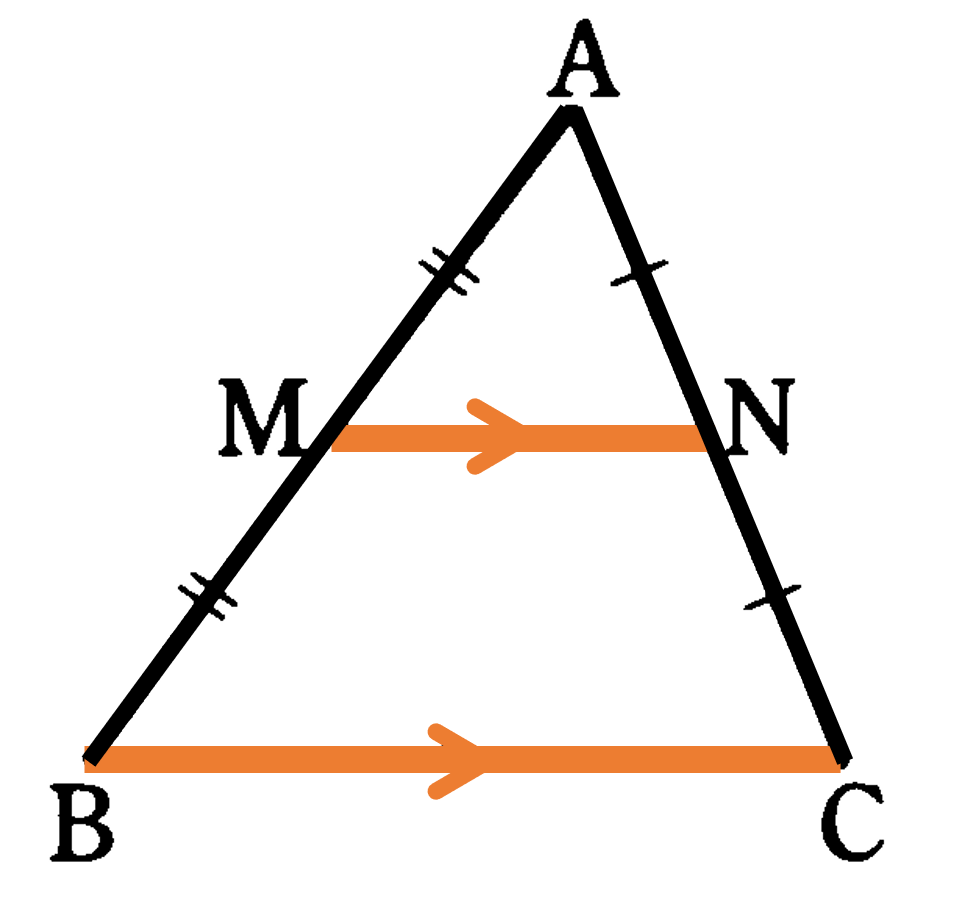
続いて三角形の各辺の中点同士を結んだ線分には、どのような性質があるのかを見てみましょう。下の図の ${\rm \triangle{ABC}}$ の2辺 ${\rm AB,AC}$ の中点をそれぞれ ${\rm M,N}$ とすると ${\rm MN}/ \! \! /{\rm BC}$, ${\rm MN}=\frac{1}{2}{\rm BC}$ という関係が成り立ちます。これは中点連結定理と呼ばれる定理です。
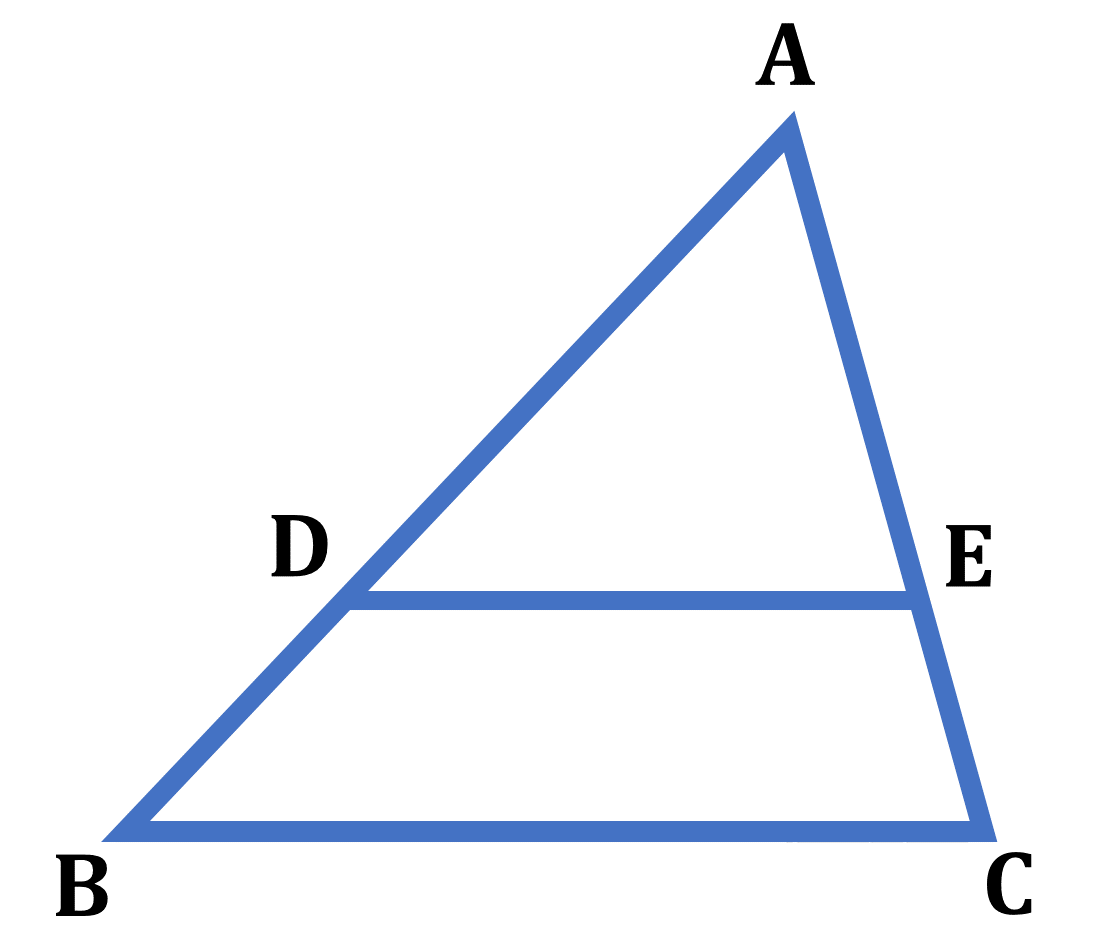
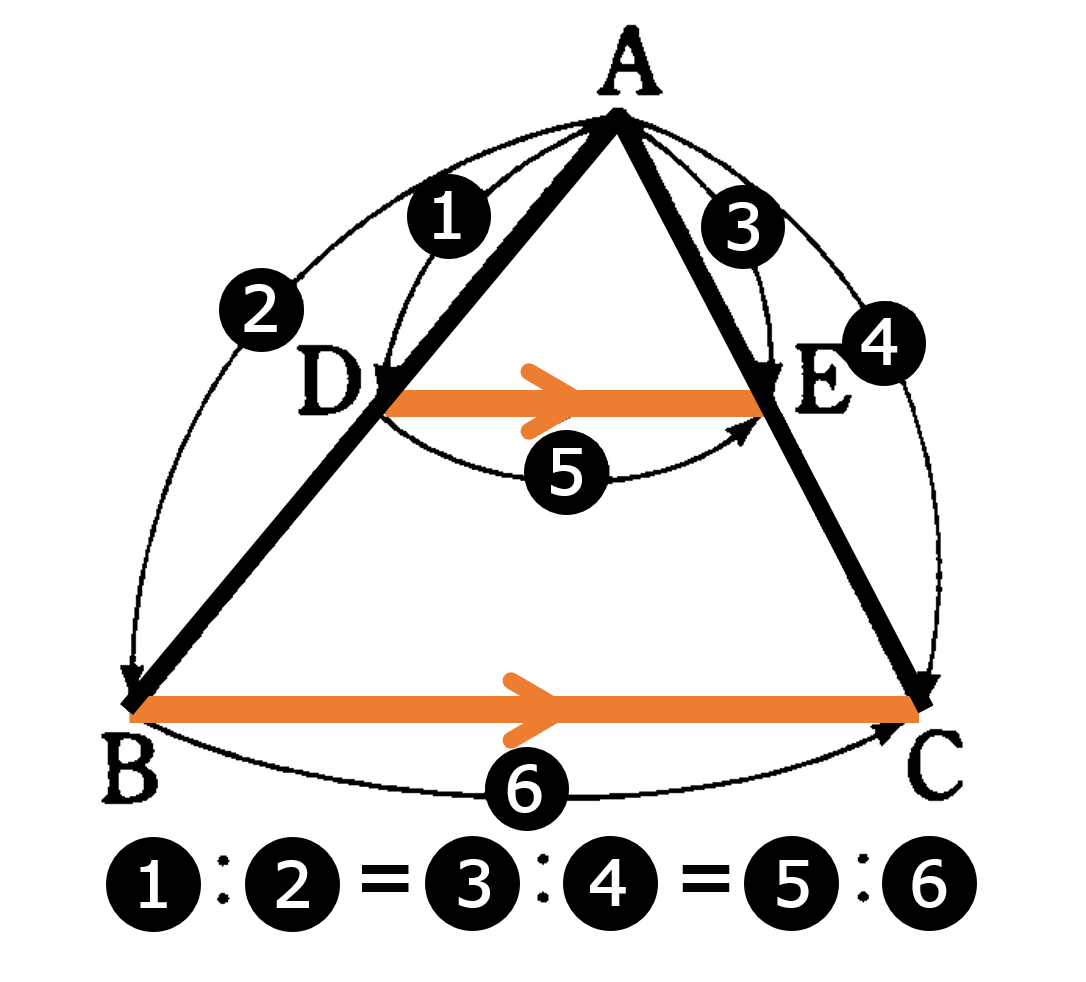
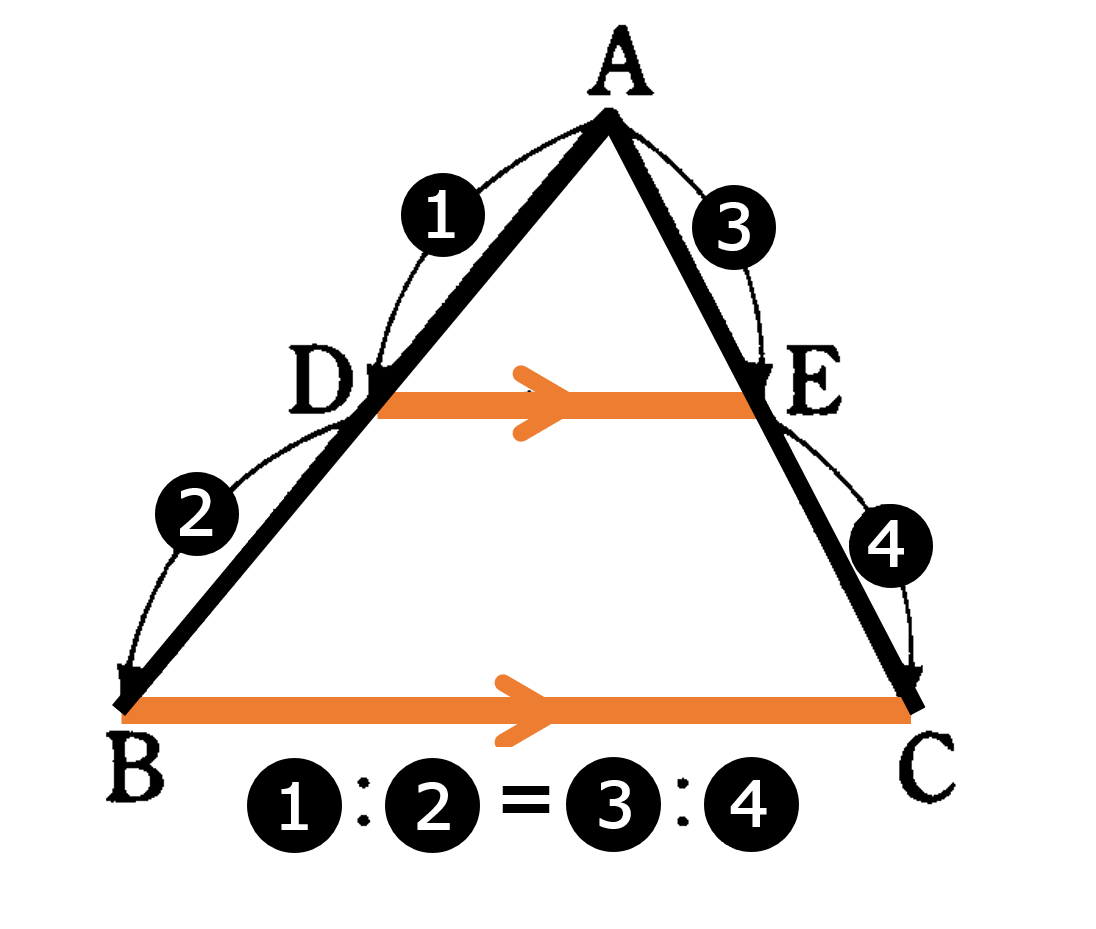
・${\rm \triangle{ABC}}$ で ${\rm DE}/ \! \! /{\rm BC}$ ならば
(1) ${\rm AD}:{\rm AB}$$={\rm AE}:{\rm AC}$$={\rm DE}:{\rm BC}$
(2) ${\rm AD}:{\rm DB}$$={\rm AE}:{\rm EC}$
・4直線 $a,b,c,d$ が平行ならば $p:p′=q:q’=r:r’$
${\rm \triangle{ABC}}$の2辺 ${\rm AB},{\rm AC}$ の中点をそれぞれ ${\rm M},{\rm N}$ とすると ${\rm MN}/ \! \! /{\rm BC},{\rm MN}=\frac{1}{2}{\rm BC}$
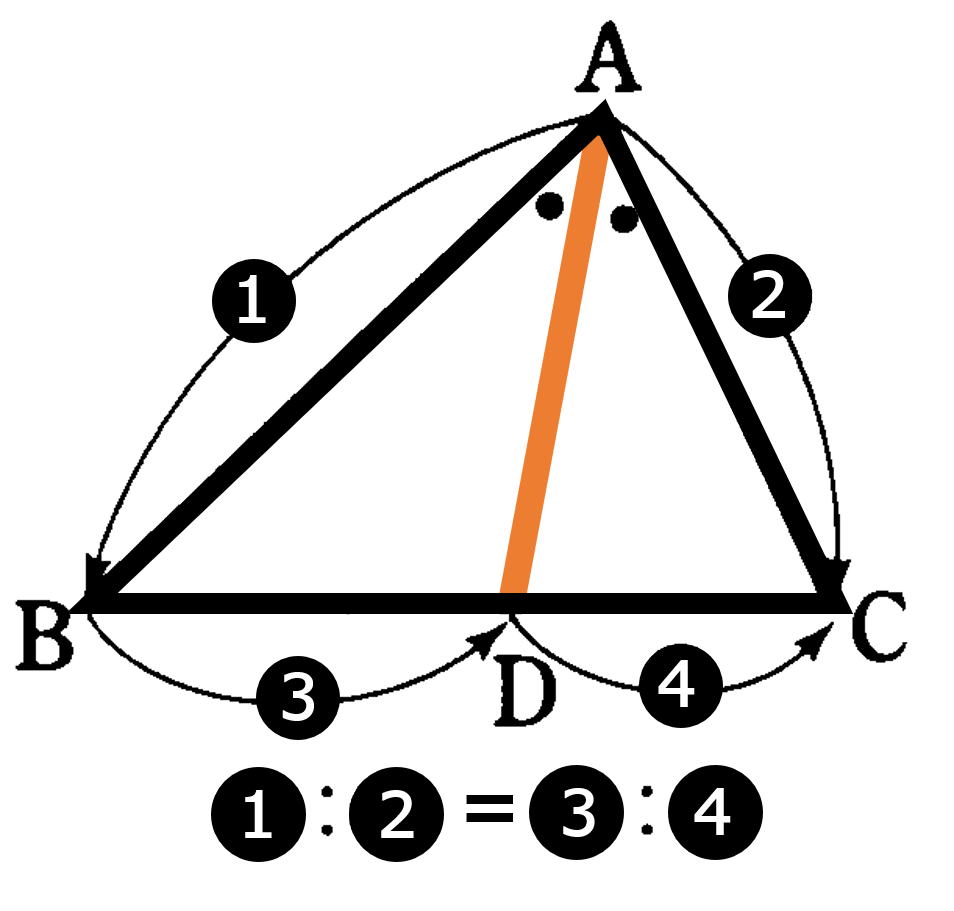
・${\rm \triangle{ABC}}$ の $\angle {\rm A}$ の二等分線 ${\rm AD}$ について ${\rm AB}:{\rm AC}={\rm BD}:{\rm DC}$
相似比と面積比・体積比
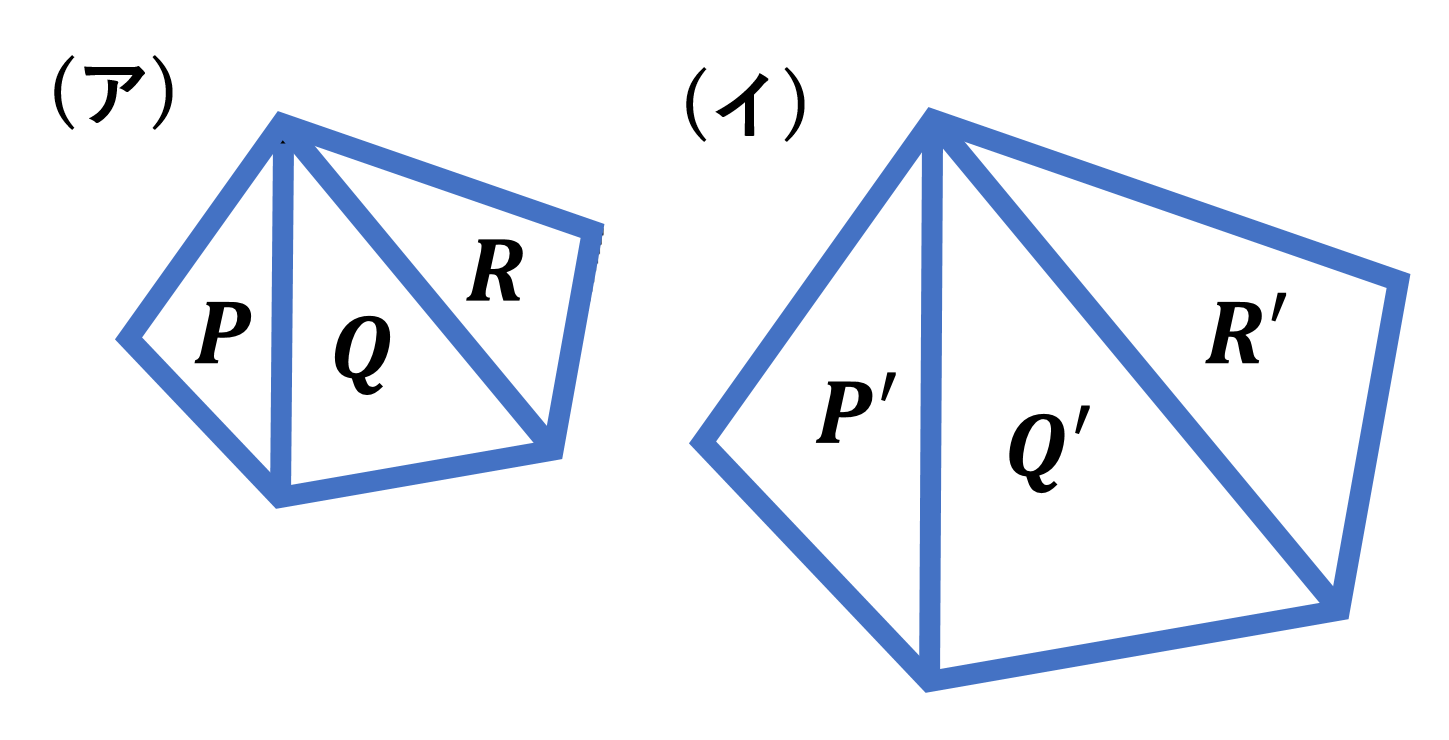
本節では、相似な図形の相似比と面積比についてみていきましょう。一般に、相似な2つの三角形で、その相似比が $m:n$ のとき その面積比は $m^2:n^2$ となります。またこの関係は三角形に限りません。下の図のように、相似な2つの多角形を、対応する頂点から出る対角線で三角形に分けると、対応する三角形はそれぞれ相似になり、相似比はもとの多角形の相似比と同じになります。例えば相似な2つの五角形(ア)(イ)で、その相似比を $2:3$ とすると、対角線で三角形に分けたときに対応する三角形はそれぞれが相似で、その相似比は $2:3$ となります。したがって、対応する三角形の面積比 ${\rm P:P’,Q:Q’,R:R’}$ は全て $2^2:3^2=4:9$ となります。つまり五角形の面積比も $4:9$ となります。このことから、一般に相似な2つの多角形で、その相似比が $m:n$ であるとき面積比は $m^2:n^2$ となることが分かります。さらに、相似な平面図形では、周の長さの比は相似比に等しく、面積比は相似比の2乗に等しくなります。
面積と線分の比:三角形の面積について:
(1) 等底なら高さの比に等しい。
(2) 等高なら底辺の比に等しい。
これらのことは底辺 $b$ 高さ $h$ の三角形の面積 $S$ が $S=\frac{bh}{2}$ であることからも分かる。
(1) 面積比 $\to$ $m^2:n^2$
(2) 体積比 $\to$ $m^3:n^3$

