🔄 最終更新日 2019年12月11日 by takara_semi
中3 > 4章:関数 $y=ax^2$
1年・2年においても、問題を解決するために関数の関係にある2つの数量を扱う方法を学びました。本章では、比例・反比例・1次関数では扱うことができない2つの数量の関係について、新しい関数 $y=ax^2$ の関係を利用する方法について学びましょう。
関数 $y=ax^2$ とそのグラフ
本節では、坂道を転がるボールのように、もしくは木から落ちたリンゴのように、時間にともなって進む距離がだんだんと増えていくような変化の様子を表現する方法について考えてみましょう。$y$ が $x$ の関数で $y=ax^2$ と表されるとき $y$ は $x$ の2乗に比例するといいます。また $y$ が $x$ の関数で2次式 $y=ax^2+bx+c$ で表されるとき $y$ は $x$ の2次関数であるといいます。$y=ax^2$ は2次関数の特別な場合であるといえます(つまり $y$ は $x$ の2乗に比例し~という問題文があった場合は $y=ax^2$ の式を考えればよいということです)。
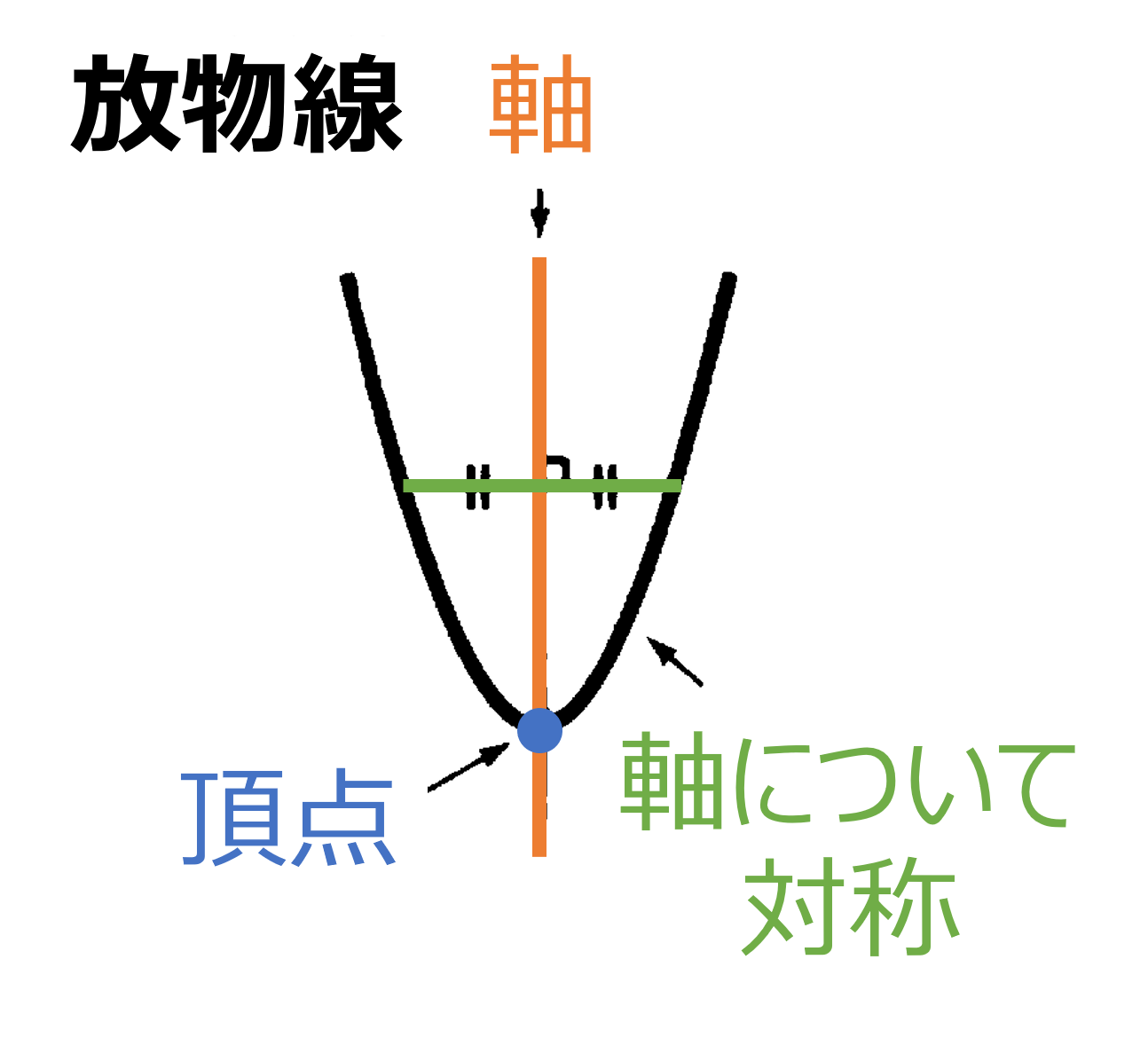
続いて関数 $y=ax^2$ のグラフについてみていきましょう。$y=ax^2$ のグラフの特徴には (1) 原点を通る。(2) $y$ 軸について対称な曲線である。(3) $a > 0$ のときは上に開いた形 $a < 0$ のときは下に開いた形になる。(4) $a$ の値の絶対値が大きいほどグラフの開きは小さい(より尖った形になる)。というようなものがあります。$y=ax^2$ のグラフは放物線といい、放物線は対称の軸をもち、対象の軸と放物線との交点を、放物線の頂点といいます。関数 $y=ax^2$ において $a > 0$ のとき $x$ の値が増加すると (1) $x < 0$ の範囲では $y$ の値は減少する。(2) $x > 0$ の範囲では $y$ の値は増加する。(3) $x = 0$ では $y$ は最小値 $0$ となります。$a < 0$ の場合は $y$ の増減が反転します(おおよそのグラフを描いて確認しましょう)。$y$ の変域を求める問題では、端点の値だけでなく、放物線の頂点($x=0,y=0$)の存在に常に注意をして解きましょう。 また関数 $y=ax^2$ では $x$ がどの値からどの値まで変化するかによって変化の割合は異なり、一定ではありません(変化の割合$=\frac{yの増加量}{xの増加量}$)。放物線の問題は受験問題でもしばしばみかけますので、グラフの特徴や利用方法などを正しく理解しておきましょう。
関数 $y=ax^2$:
(1) $y$ は $x$ の2乗に比例する。
(2) $x$ の値が$2$倍,$ 3$倍, … ,$p$ 倍になる $\to$ $y$ の値は $2^2$ 倍, $3^2$ 倍, … ,$p^2$ 倍 になる。
(1) 原点を通る。
(2) $y$ 軸について対称になる。
(3) 放物線である。
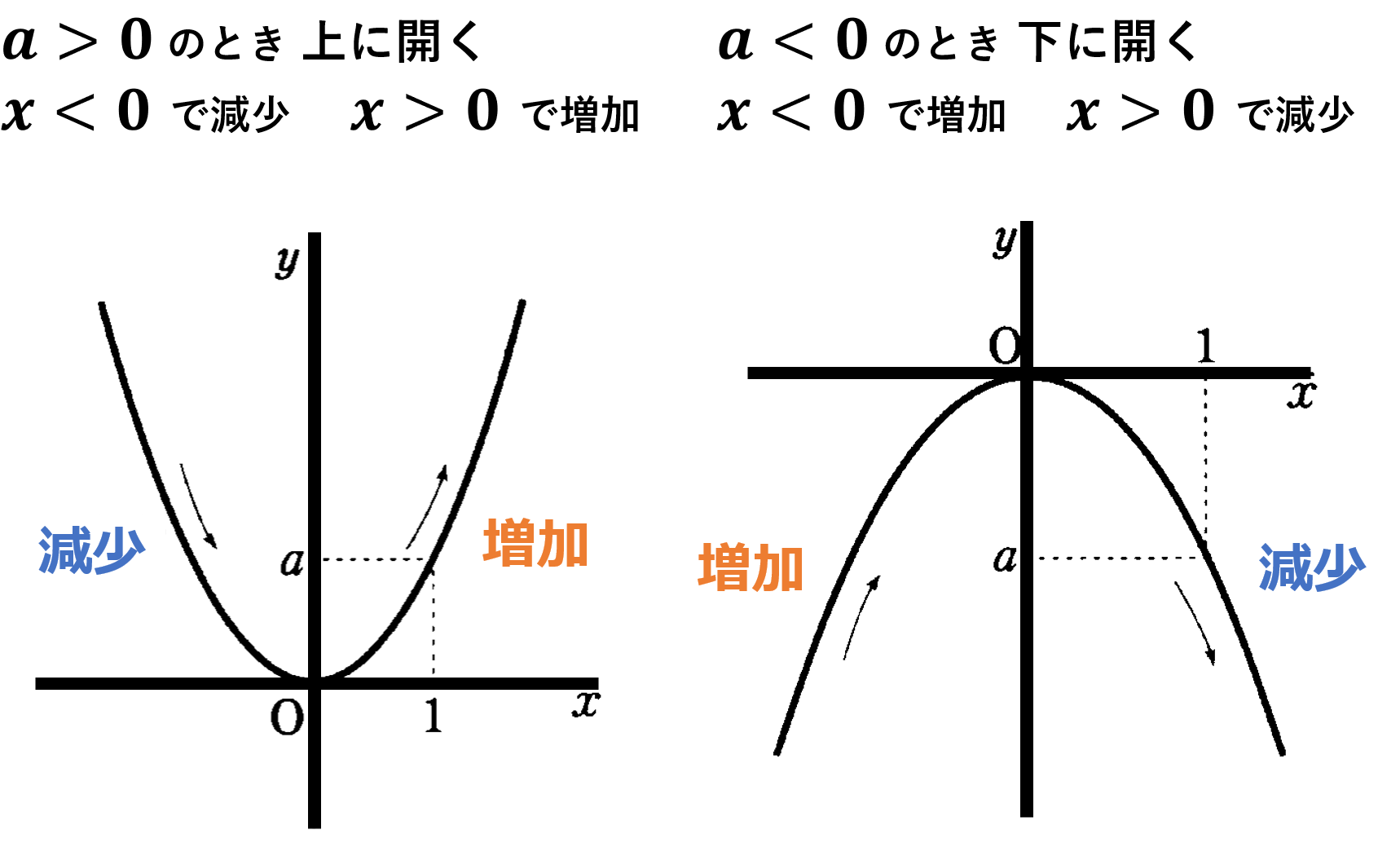
変域を求めるにはグラフを利用して考える。「端の点」と「頂点」に注目すれば分かる。
関数 $y=ax^2$ の利用
本節では、身の回りの問題を関数 $y=ax^2$ とそのグラフを利用して解決する方法について考えてみましょう。例えば、関数 $y=ax^2$ を利用することで「加速する電車が一定速度で走る車に追いつくまでの時間」を計算したりすることができます。他にも数多くのことがらを、関数 $y=ax^2$ を利用することで解決することができます。演習を繰り返して着実に実力を付けていきましょう。
放物線と直線の交点:放物線 $y=ax^2$ と直線 $y=mx+n$ の交点:
STEP1:$y$ を消去し2次方程式 $ax^2=mx+n$ を導く。
STEP2:その方程式を解き $x$ の値を求める。そして得られて $x$ を与式に代入して $y$ の値を求める。
STEP3:$(x,y)$ の組にして交点の座標とする。
いろいろな関数
本節では、身の回りにある色々な関数について考えてみましょう。例えば電車の乗車距離 $x$ と運賃 $y$ の関係は、グラフに表すと $y$ が飛び飛びの値をとる関数になります。このように、身の回り様々な数量の関係をみいだし、その関数を利用して問題を解決してみましょう。
いろいろな関数の中にはそのグラフがつながっていないものもある。
例1)電車に乗る距離 $x$ kmと運賃 $y$ 円の関係。
例2)駐車時間 $x$ 分と駐車料金 $y$ 円の関係。
実際にグラフを描いてみると不連続(階段状)であることが分かる。

