🔄 最終更新日 2019年12月11日 by takara_semi
中2 > 4章:図形の性質と合同
本章では簡単な図形の性質から複雑な図形の性質まで、順を追って正しく理解していくことが目的です。図形の性質やその表現を習得することで、ロボット工学やコンピュータグラフィックスなど、あなたの数学の知識を活用できる場がより一層広くなることでしょう。
平行線と角
本節では平行線と角の性質を説明する(導く)ことを考えます。まず2直線が交わってできる角についてみていきます。2つの直線が交わると、その交点の周りに角ができます。それらの角のうち、向かい合っている角を対頂角といい、その性質として「対頂角は等しい」ということがいえます(その理由を説明できるように:$180^{\circ}-$(共通の角) が等しいことから説明可)。続いて2つの直線に1つの直線が交わってできる角について、その位置関係によって同位角と錯角と呼ばれる角があります。錯角は「たがいちがいの角」という意味です。位置関係と角の呼び方、およびその特徴については要点を確認してください。とくに平行線と同位角・錯角の特徴は重要なポイントなので、正しく理解しておきましょう。平行線の性質として、2直線に1つの直線が交わるとき (1) 2直線が平行ならば同位角は等しい (2) 2直線が平行ならば錯角は等しい ということがいえます。またこれらの性質から、2直線が平行線になる条件として (1) 同位角が等しければその2直線は平行である (2) 錯角が等しければその2直線は平行である ということがいえます。
対頂角・同位角・錯角:
(1) 対頂角は等しい
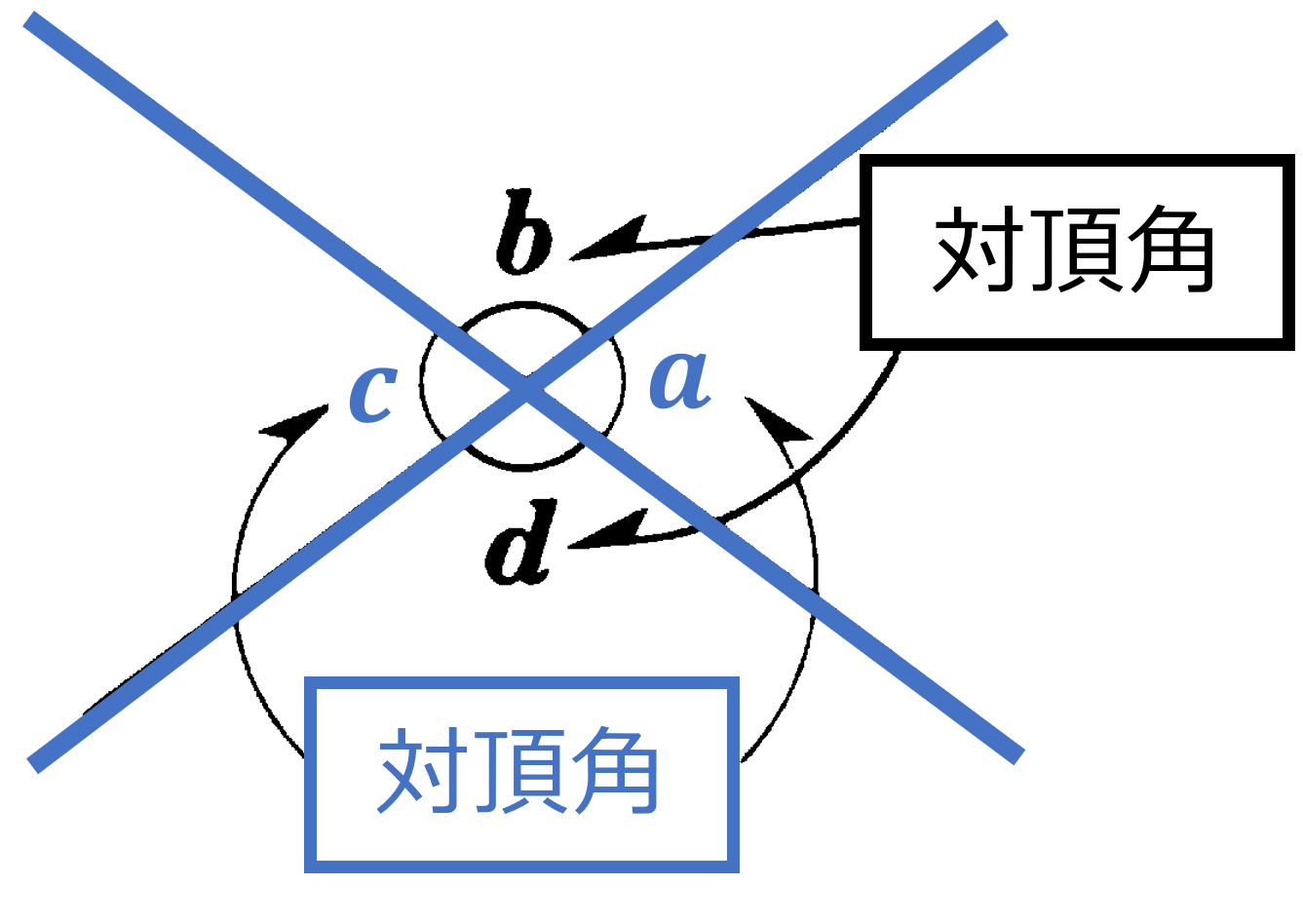
(2) 2直線に1直線が交わってできる角
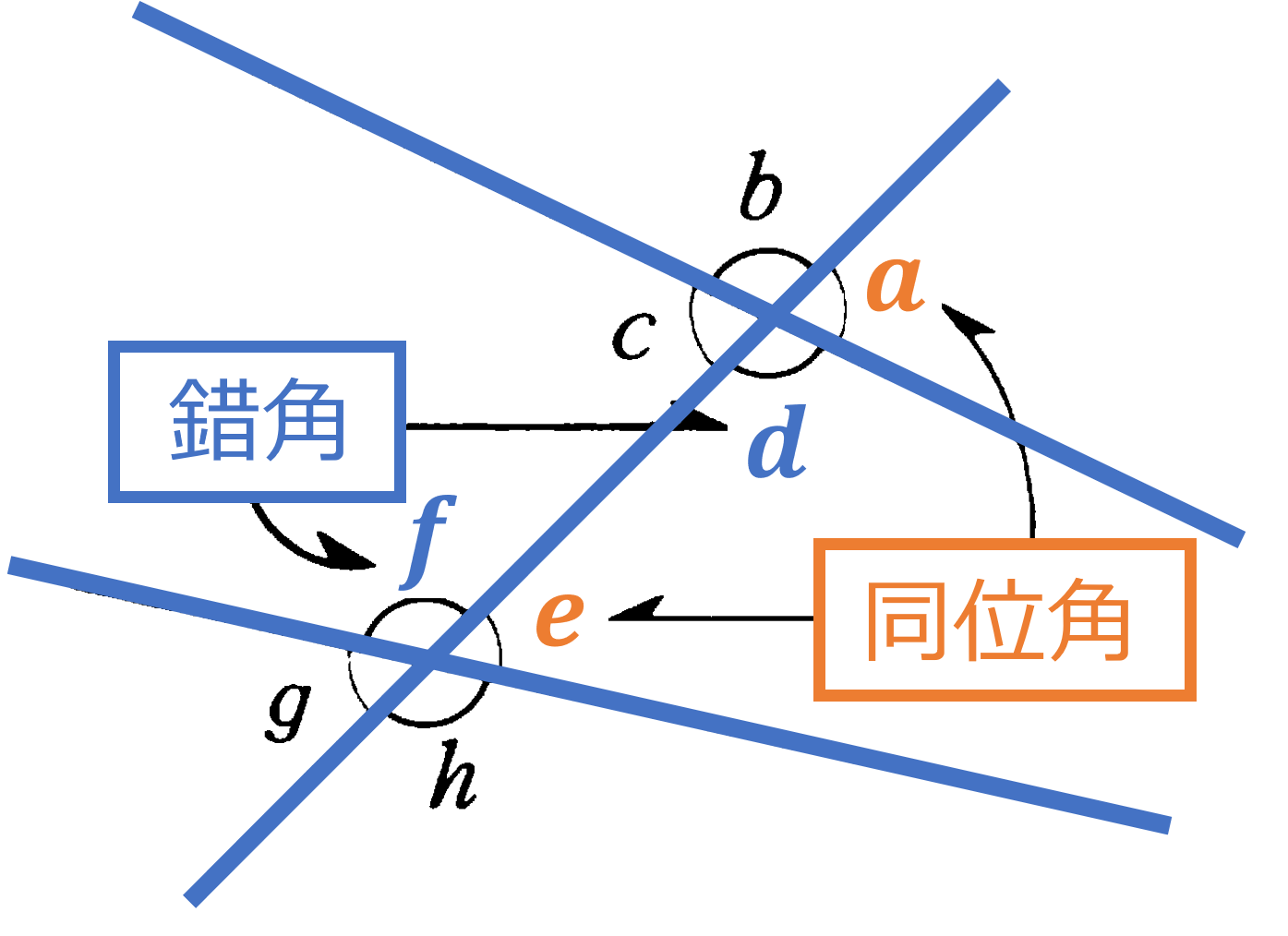
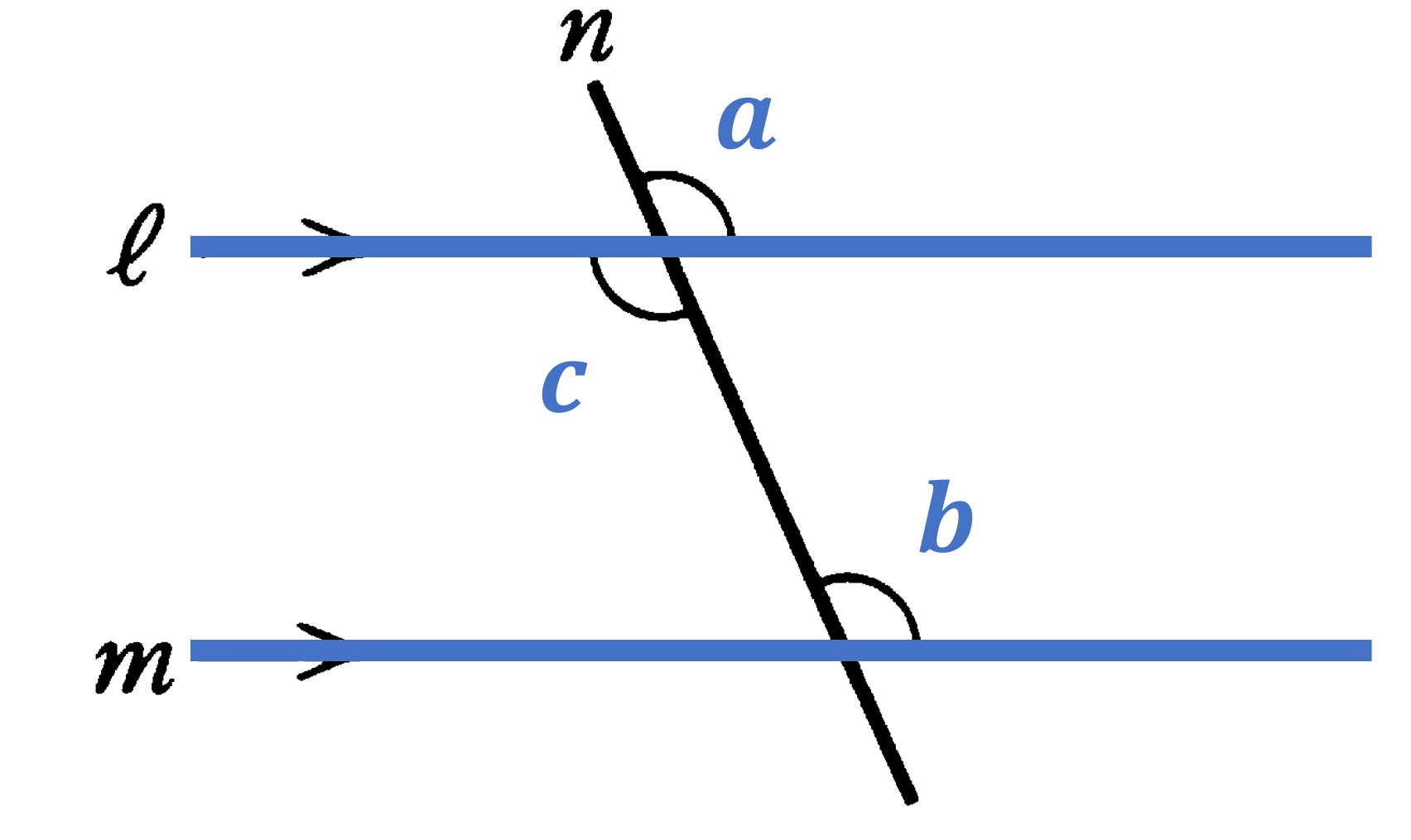
平行線と同位角・錯角:
(1) 平行 $\iff$ 同位角が等しい:$\ell / \! \! / m \iff \angle a=\angle b$
(2) 平行 $\iff$ 錯角が等しい:$\ell / \! \! / m \iff \angle c=\angle b$
多角形の角
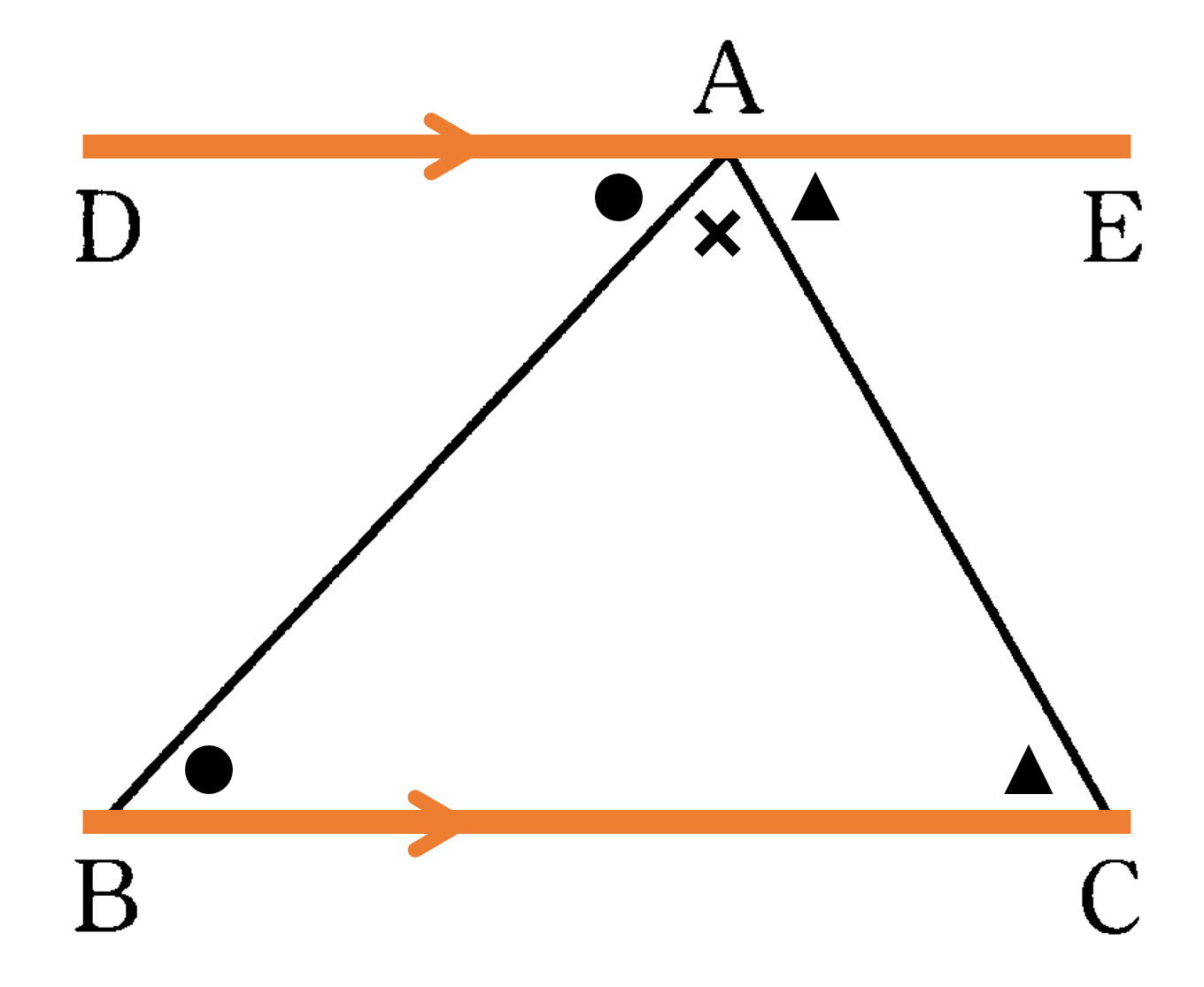
本節では多角形の角について考えてみましょう。ここで多角形というときにはへこんだ部分があるものは考えないものとします。多角形の2辺が作る内側の角を内角、1つの辺と隣りの辺の延長とが作る角を、その頂点の外角といいます。次に、平行線と角の性質を利用して、三角形の内角の和が $180^{\circ}$ であることを説明してみましょう。ある ${\rm \triangle{ABC}}$ の頂点Aを通り、辺BCに平行な直線DEをひきます(説明や計算の理解を助けるためにひく、このような線を補助線といいます)。このとき、次のことが成り立ちます。
(1) 平行線の錯角は等しいから ${\rm \angle ABC}={\rm \angle BAD} \ -①$
(2) 平行線の同位角は等しいから ${\rm \angle BCA}={\rm \angle CAE} \ -②$
したがって ${\rm \triangle{ABC}}$ の内角の和は $①②$ より
${\rm \angle ABC}+{\rm \angle BCA}+{\rm \angle CAB}$$={\rm \angle BAD}+{\rm \angle CAE}+{\rm \angle CAB}$$=180^{\circ}$
となることがいえます。他にも多角形の角の性質は多くありますので、要点でその内容を確認しておきましょう。
三角形の内角と外角:
(1) 内角の和は $180^{\circ}$
(2) 外角はその隣にない2つの内角の和に等しい。
(3) 外角の和は $360^{\circ}$
多角形の内角と外角:
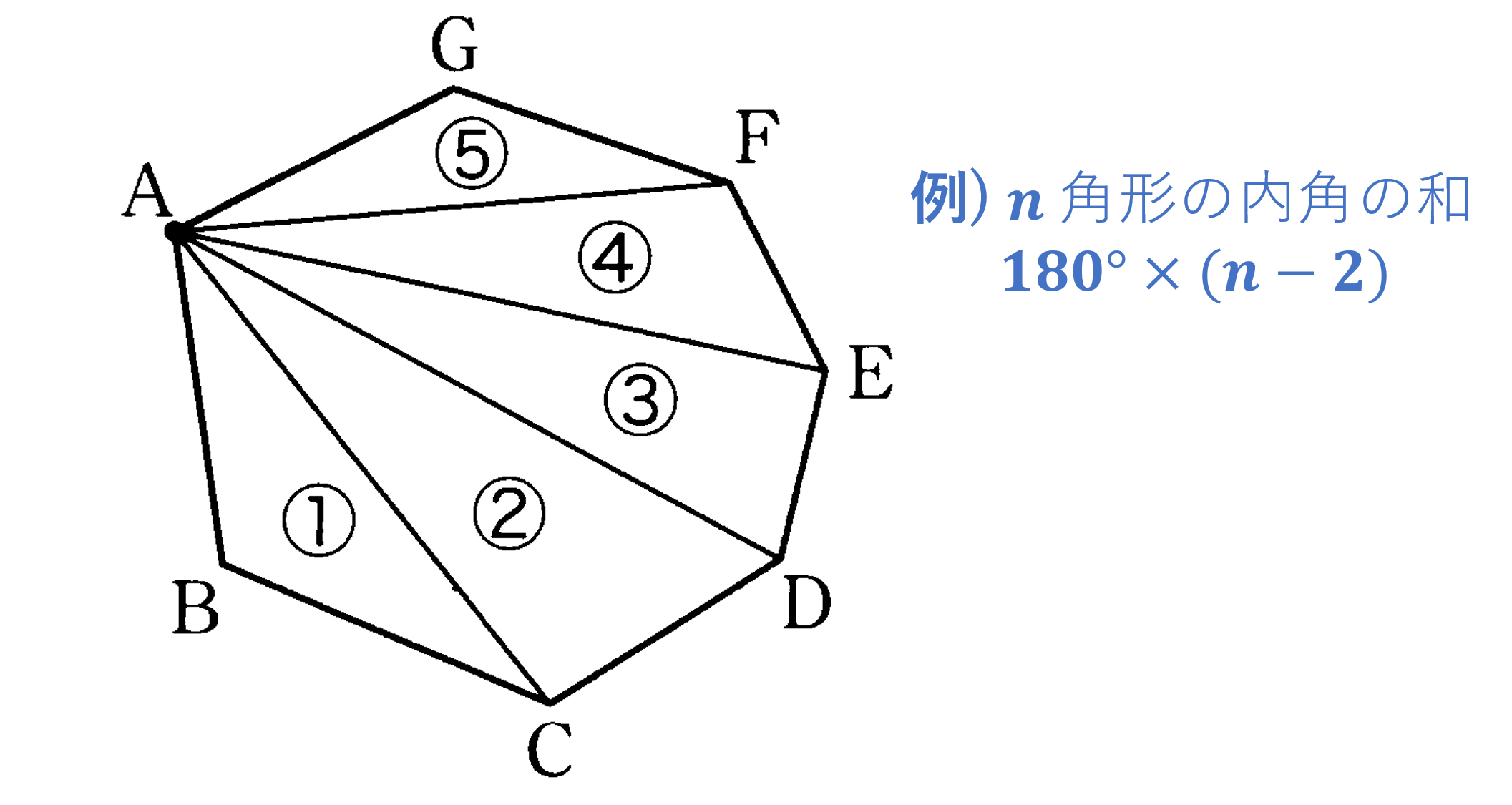
(1) $n$角形の内角の和 $180^{\circ}×(n-2)$
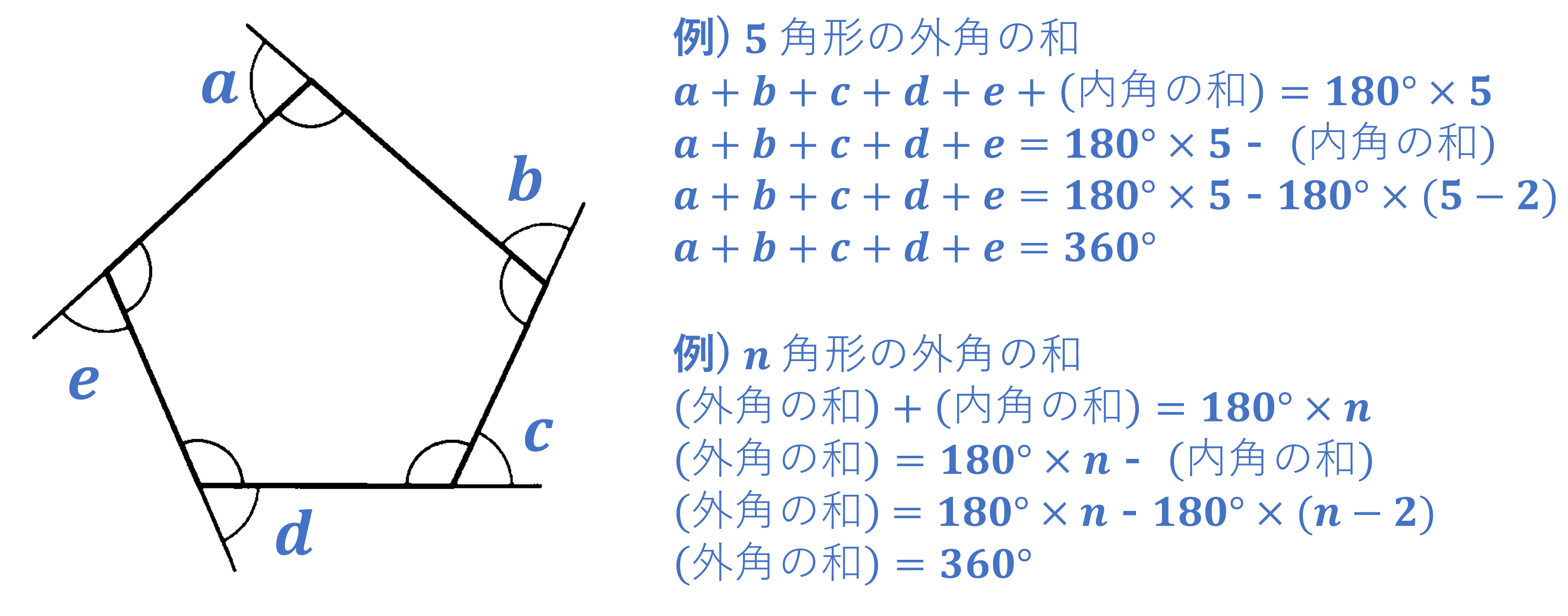
(2) 多角形の外角の和 $360^{\circ}$
三角形の合同
本節では図形の合同について考えてみましょう。平面上の2つの図形について、一方を移動・回転・反転することで他方に重ね合わせることができるとき、この2つの図形は合同であるといいます。そして合同であることを記号 $\equiv$ で表します。例えば 四角形ABCD $\equiv$ 四角形EFGH のようにかき、対応する頂点の名前の順に示します(頂点AとE、頂点BとF…がそれぞれ対応します)。また合同な図形では対応する線分や角は等しくなります。
ここからは平面図形の中でも特に三角形の合同について考えていきます。様々な三角形を観察すると、2つの三角形が合同かどうかを判断するには次の合同条件を満たすかどうかを調べればよいことが分かります。(1) 3組の辺がそれぞれ等しい (2) 2組の辺とその間の角がそれぞれ等しい (3) 1組の辺とその両端の角がそれぞれ等しい。2つの三角形の合同を調べるときには、これらの合同条件のいずれかに当てはまれば合同であると判断することができます。この合同条件は文言も含めて正しく覚えて使えるようになりましょう。合同の意味を理解していれば、言葉も自然と暗記できることかと思います。
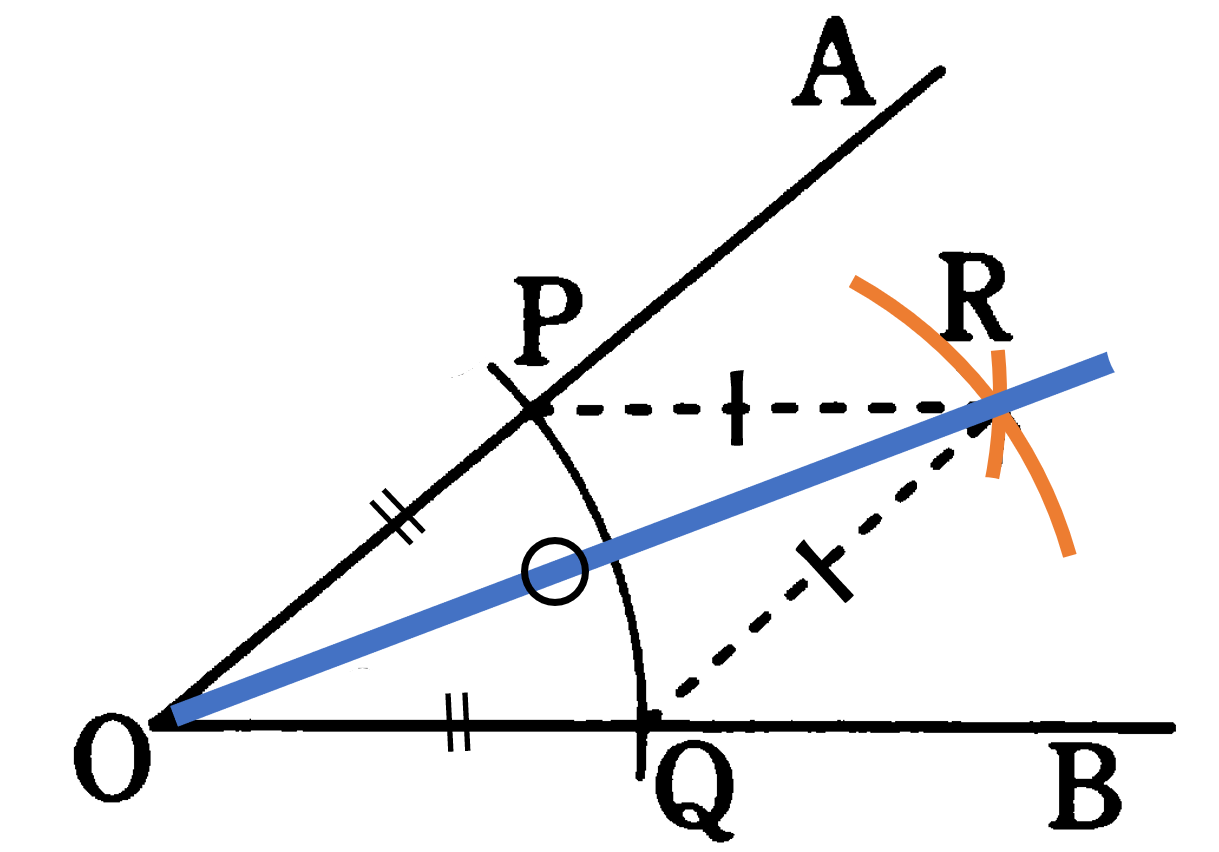
最後に三角形の合同条件を利用した証明について考えてみましょう。三角形の合同条件を利用することで、角の二等分線の作図が正しいことを確かめましょう。
下の図に角の二等分線の作図によって描かれた2つの三角形 ${\rm \triangle{OPR}}$, ${\rm \triangle{OQR}}$ を示します。この図で ${\rm \triangle{OPR}}$, ${\rm \triangle{OQR}}$ において
コンパスを用いた作図であるため
${\rm OP}={\rm OQ} ―①$
${\rm PR}={\rm QR} ―②$
また共通する辺であるため
${\rm RO}={\rm RO} ―③$
よって $①②③$ より 3組の辺がそれぞれ等しいから ${\rm \triangle{OPR}}$$\equiv$${\rm \triangle{OQR}}$ がいえ、合同な図形の対応する角は等しいことから ${\rm \angle ROP}={\rm \angle ROQ}$ となり、ORは ${\rm \angle POQ}$ の二等分線であるといえます(証明終了)。
このような、三角形の合同条件を利用した証明の問題は入試問題としてもよく取り上げられます。角や平行線の性質、等式の性質、面積や体積の公式なども証明の根拠として利用されることがあります。これらも合わせて、正しく理解して着実に身に着けていきましょう。
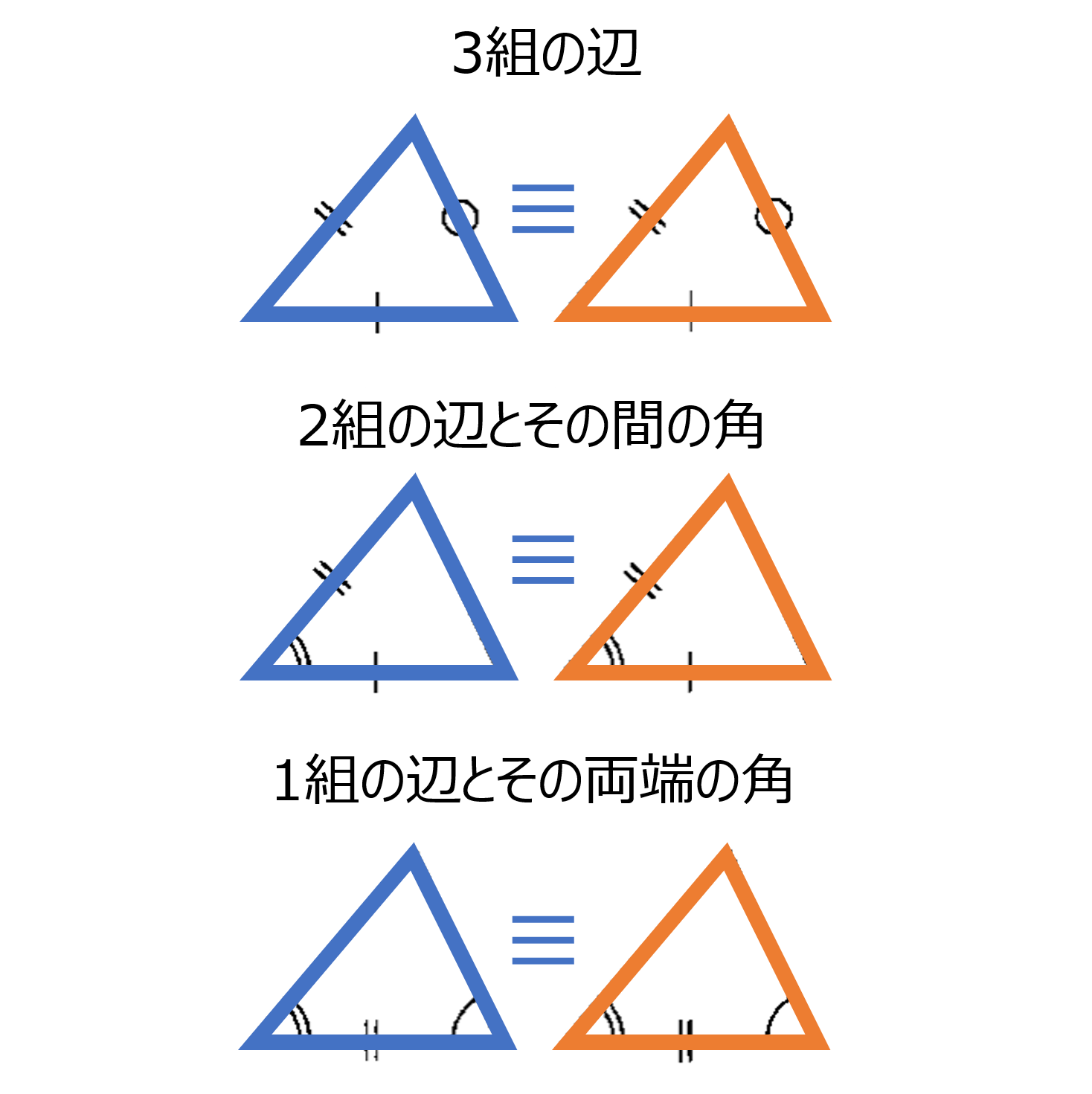
三角形の合同条件:次の(1)(2)(3)いずれかが成り立てば合同。
(1) 3組の辺 (2) 2組の辺とその間の角 (3) 1組の辺とその両端の角
例
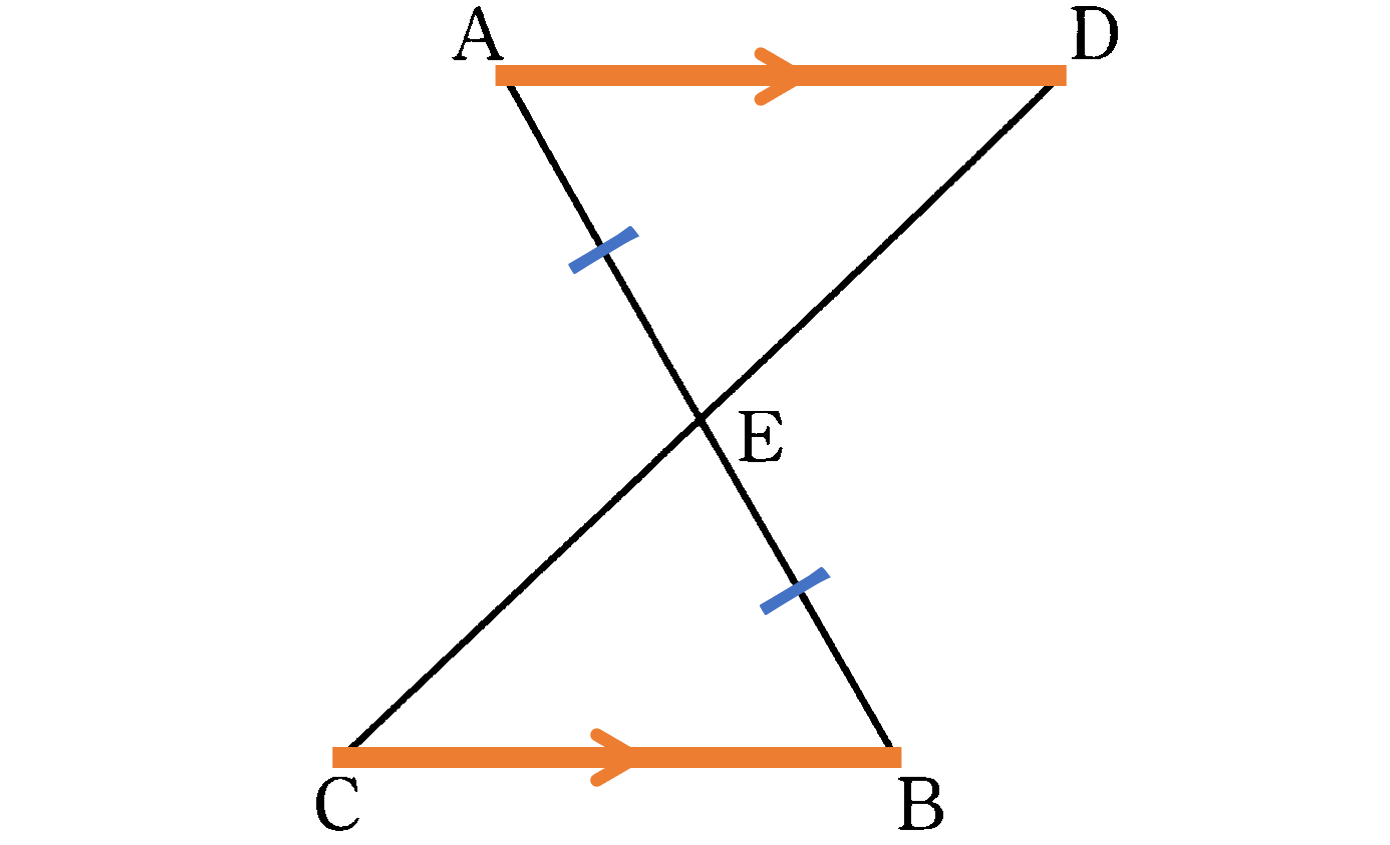
下図で ED $=$ EC となることを証明する $\to$ 仮定(条件)から結論(三角形の合同)を導く。
${\rm \triangle{AED}}$ と ${\rm \triangle{BEC}}$ において
仮定から
${\rm EA}={\rm EB} ―①$
対頂角は等しいから
${\rm \angle AED}={\rm \angle BEC} ―②$
平行線の錯角は等しいから
${\rm \angle EAD}={\rm \angle EBC} ―③$
$①②③$ より 1組の辺とその両端の角がそれぞれ等しいから
${\rm \triangle{AED}}$$\equiv$${\rm \triangle{BEC}}$
合同な図形の対応する辺は等しいから
${\rm ED}={\rm EC}$ (証明終了)
証明
この節では「証明」について再確認していきましょう。証明とは、先の節であった「平行線と角の性質を利用して、三角形の内角の和が $180^{\circ}$ であることを説明する」例のように「あることがらが成り立つ理由」を「すでに正しいと分かっている性質を根拠にして示す」ことをいいます。この例では「三角形の内角の和が $180^{\circ}$ になる理由」を「自明な平行線の性質を根拠にして示す」という証明をしたといえます。このように平行線の性質や三角形の性質を利用して証明可能な図形の性質として、次のようなものがあります。「三角形の内角の和は $180^{\circ}$ である」「三角形の外角は、それと隣り合わない2つの内角の和に等しい」「$n$ 角形の内角の和は $180^{\circ} \times (n-2)$ である」「多角形の外角の和は $360^{\circ}$」。平行線の性質 $\to$ 三角形の内角の和 $\to$ 多角形の内角の和 $\to$ 多角形の外角の和 の順で証明できます。証明や図形の問題になれるために、それぞれの性質を自分で証明できるようになっておきましょう。
仮定と結論:ことがら「(ア)ならば(イ)」について考える。
(ア):与えられて分かっていること $\to$ (ア)の部分が仮定
(イ):(ア)から導こうとしていること $\to$ (イ)の部分が結論
数学が面白くなる動画―12
証明を間違えると大変なことになる?証明を積み立てることで数学はどんどん楽しくなる。

