🔄 最終更新日 2019年12月11日 by takara_semi
中2 > 5章:三角形と四角形
本章では三角形と四角形の性質を調べます。特に線対称な図形である二等辺三角形や、点対称な図形である平行四辺形の性質を詳しく調査し、その性質を証明してみましょう。
三角形
本節では三角形の性質について考えてみましょう。まずは二等辺三角形についてです。二等辺三角形とは「2つの辺が等しい三角形」のことです。このように、言葉の意味をはっきりと述べたものを定義といいます。この定義をもとにして、より発展的な事実を証明していくことで、その性質をより深く知ることができるのです。例えば、二等辺三角形の2つの角は等しいということも、この定義を根拠に、合同条件を利用して証明することができます。また二等辺三角形で、長さの等しい2つの辺の間の角を頂角といい、頂角に対する辺を底辺、底辺の両端の角を底角といいます。「二等辺三角形の底角は等しい」「三角形の内角の和は $180^{\circ}$」「二等辺三角形の頂角の二等分線は底辺を垂直に2等分する」等の性質は、当然の事実として証明の根拠としても利用されますが、定義ではありません。これらは定義などを根拠に証明された性質のひとつであり、このような証明された大切なことがらを定理といいます(高度な数学は、この確かな根拠に裏付けられた「定理」の積み重ねによって成り立っているといっても過言ではありません)。このような定理を利用することで、複雑な問題を簡単に解決することができるようになります。
次に正三角形について考えてみましょう。正三角形とは「3つの辺が等しい三角形」のことです。これが正三角形の定義です。この定義から容易に「正三角形の3つの角は等しい」という定理を証明することができます(二等辺三角形の底角が等しいという定理を利用します)。(※ 三角形は角によって3つに分類することができます。3つの角がすべて鋭角( $0^{\circ}$ より大きく $90^{\circ}$ より小さい角)のものを鋭角三角形、1つの角が直角のものを直角三角形、1つの角が鈍角( $90^{\circ}$ より大きく $180^{\circ}$ より小さい角)のものを鈍角三角形といいます。)
続いて、三角形にどんな条件が加わると二等辺三角形になるかを考えてみます。先に「三角形の2辺が等しいとき、2つの角は等しい」ということを証明しましたが、逆の「2つの角が等しい三角形の2辺は等しい」も成り立つといえるでしょうか。これは図形の合同を利用することで証明可能です。つまり二等辺三角形になるための条件の定理として「三角形の2つの角が等しければ、その三角形は、等しい2つの角を底角とする二等辺三角形である」ということがいえます。同様に、正三角形になる条件の定理として「3つの角が等しい三角形は正三角形である」ということもいえます。ここで、定理の逆というものについて考えてみましょう。「三角形の2つの辺が等しい時、2つの角は等しい…①」ことと「三角形の2つの角が等しいとき、2つの辺は等しい…②」ことは、定理の仮定と結論を入れかえたものであり、このようなものを定理の逆といいます。すなわち②は①の逆であり、①は②の逆です。また「正しいことの逆」がいるも正しいとは限りません。例えば「 $x≧7$ ならば $x > 5$ 」ということがらは正しいですが、逆の「 $x > 5$ ならば $x≧7$ 」ということがらは $x=6$ では成り立たず、正しいといえません。このような、あることがらが成り立たない例を反例といい、あることがらが正しくないことを示すには反例を1つあげればよいといえます。このように、ある定理の逆が正しいということをいうためには、改めてその正しさを証明する必要があるのです。
最後に直角三角形について考えていきましょう。直角三角形の直角に対する辺は斜辺といいます。また直角三角形は「三角形の合同条件」に加えて、次の2つの特別な合同条件を使うことができます。(1) 斜辺と1つの鋭角がそれぞれ等しい。 (2) 斜辺と他の1辺がそれぞれ等しい。 2つの直角三角形の合同を考える時は、この特別な合同条件を上手く活用しましょう。
二等辺三角形の定義:2辺が等しい三角形
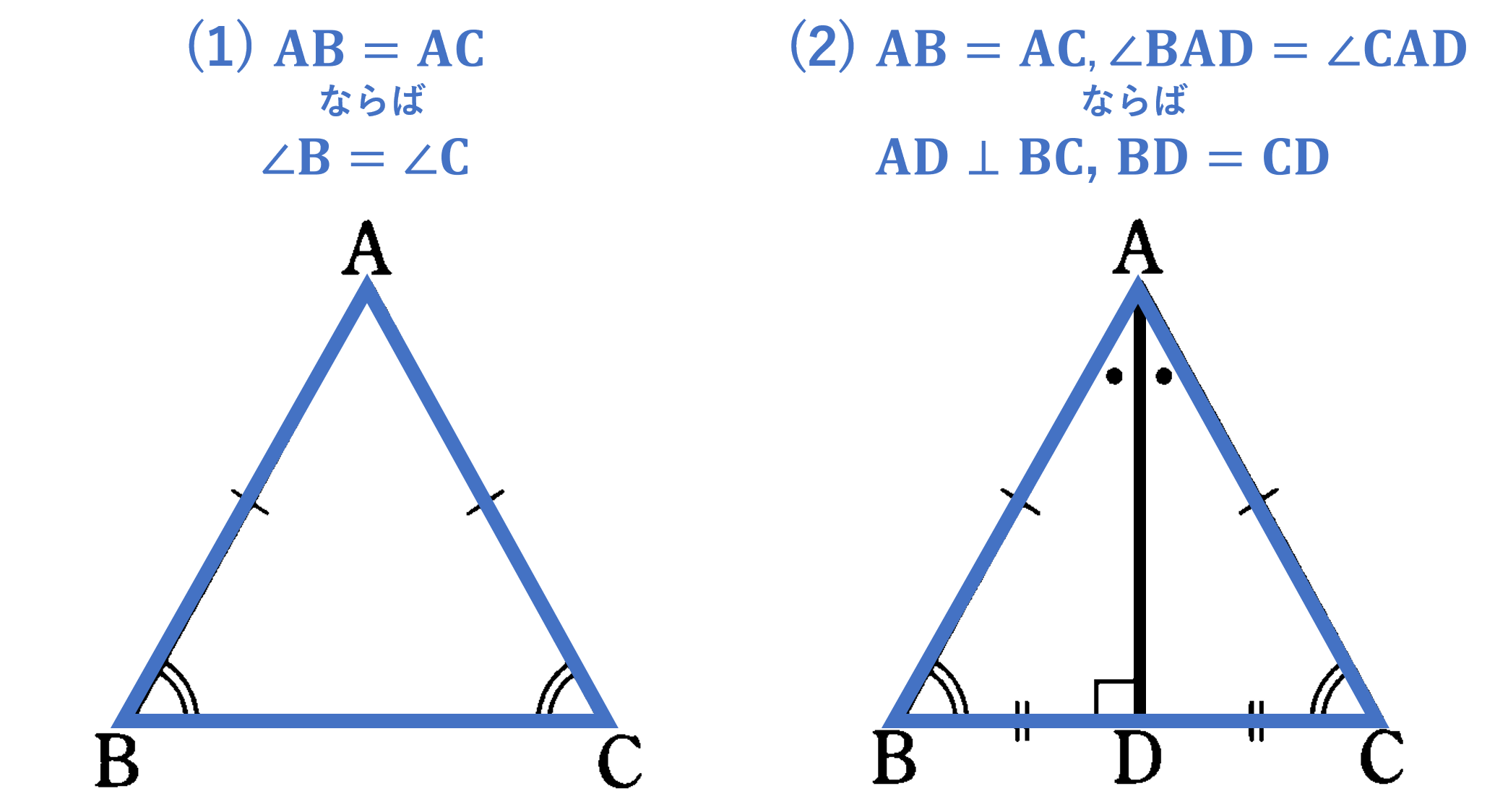
【定理】
(1) ${\rm AB}={\rm AC}$ ならば $\angle {\rm B}=\angle {\rm C}$
(2) ${\rm AB}={\rm AC}$, $\angle {\rm BAD}=\angle {\rm CAD}$ ならば ${\rm AD} \perp {\rm BC}$, ${\rm BD}={\rm CD}$
(3) $\angle {\rm B}=\angle {\rm C}$ ならば ${\rm AB}={\rm AC}$
【定理】
${\rm \triangle{ABC}}$ で ${\rm AB}={\rm BC}={\rm CA}$ $\iff$ $\angle {\rm A}=\angle {\rm B}=\angle {\rm C}$
直角三角形の定義:1つの内角が直角である三角形
直角三角形の合同条件:一般の合同条件の他に(1)(2)いずれかが等しい時にも合同。 (1) 斜辺と1つの鋭角 (2) 斜辺と他の1辺
四角形
本節では四角形、特に平行四辺形の性質についてみていきます。四角形の向かい合う辺を対辺向かい合う角を対角といいます。平行四辺形は以下のように定義づけられています。「平行四辺形とは2組の対辺がそれぞれ平行な四角形のことである。」平行四辺形 ${\rm ABCD}$ を ${\rm ▱ABCD}$ と表すこともあります。平行四辺形の性質(定理)として次の3つがあります。(1) 2組の対辺はそれぞれ等しい。 (2) 2組の対角はそれぞれ等しい。 (3) 対角線はそれぞれの中点で交わる。 これらの性質は「平行線と錯覚・対頂角・同位角」や「合同な図形」の知識を利用することで証明することができますので、1度確認しておきましょう。次に平行四辺形になるための条件についてみていきましょう。四角形は次のいずれかが成り立てば平行四辺形となります。(1) 2組の対辺がそれぞれ平行。…(定義) (2) 2組の対辺がそれぞれ等しい。 (3) 2組の対角がそれぞれ等しい。 (4) 対角線がそれぞれの中点で交わる。 (5) 1組の対辺が平行でその長さが等しい。
続いて、特別な平行四辺形である「長方形」「ひし形」「正方形」についてみていきます。それぞれの図形の定義は次の通りです。「長方形とは、4つの角が全て等しい四角形のことである」もしくは「長方形とは、4つの角が全て直角である四角形のことである」。「ひし形とは、4つの辺が全て等しい四角形のことである。」「正方形とは、4つの角が全て等しく、4つの辺が全て等しい四角形のことである」もしくは「正方形とは、4つの角が全て直角で、4つの辺が全て等しい四角形のことである。」 これらの定義からもわかるように、長方形やひし形は平行四辺形の特別な場合と考えることができます。また、長方形であり、ひし形でもある四角形が正方形です。
最後に、それぞれの図形の対角線の性質について考えてみましょう。長方形は対角線が等しくなります。ひし形の対角線は垂直に交わります。また、長方形の対角線の性質から考えると、直角三角形の斜辺の中点はこの三角形の3つの頂点から等しい距離になることが分かります。これらの性質を上手く活用して、図形に関する問題を工夫して解決していきましょう。
平行四辺形の定義:2組の対辺がそれぞれ平行な四角形
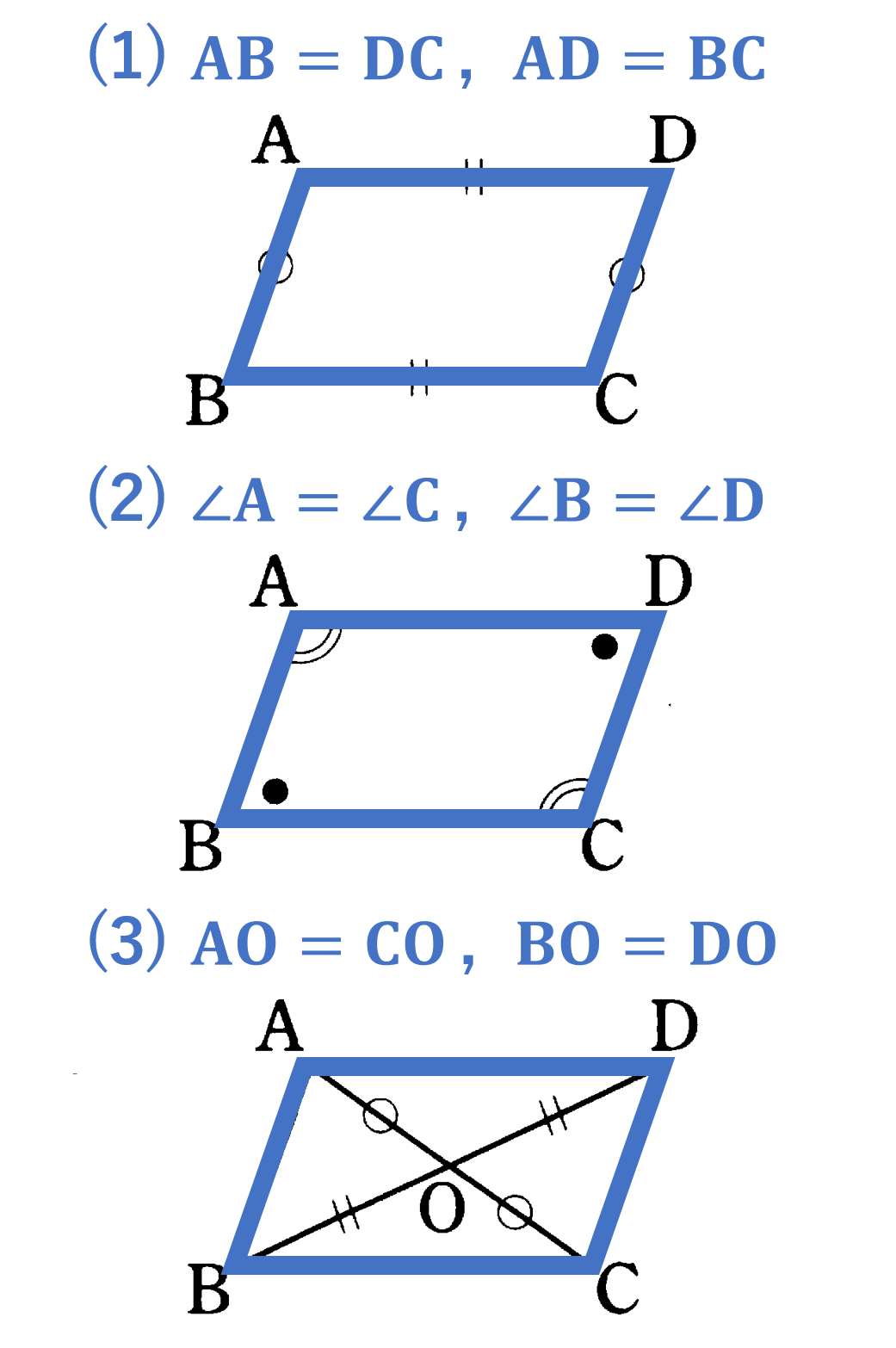
【定理】
(1) 2組の対辺はそれぞれ等しい。 ${\rm AB}={\rm DC},{\rm AD}={\rm BC}$
(2) 2組の対角はそれぞれ等しい。 $\angle {\rm A}=\angle {\rm C},\angle {\rm B}=\angle {\rm D}$
(3) 対角線がそれぞれの中点で交わる。 ${\rm AO}={\rm CO},{\rm BO}={\rm DO}$
平行四辺形になる条件:
(1) 2組の対辺がそれぞれ平行である。(=定義)
(2) 2組の対辺がそれぞれ等しい。
(3) 2組の対角がそれぞれ等しい。
(4) 対角線がそれぞれの中点で交わる。
(5) 1組の対辺が平行でその長さが等しい。
長方形:4つの角が等しい四角形。
(1) 長方形は平行四辺形。
(2) 1つの角が $90^{\circ}$
(3) 対角線の長さが等しい。

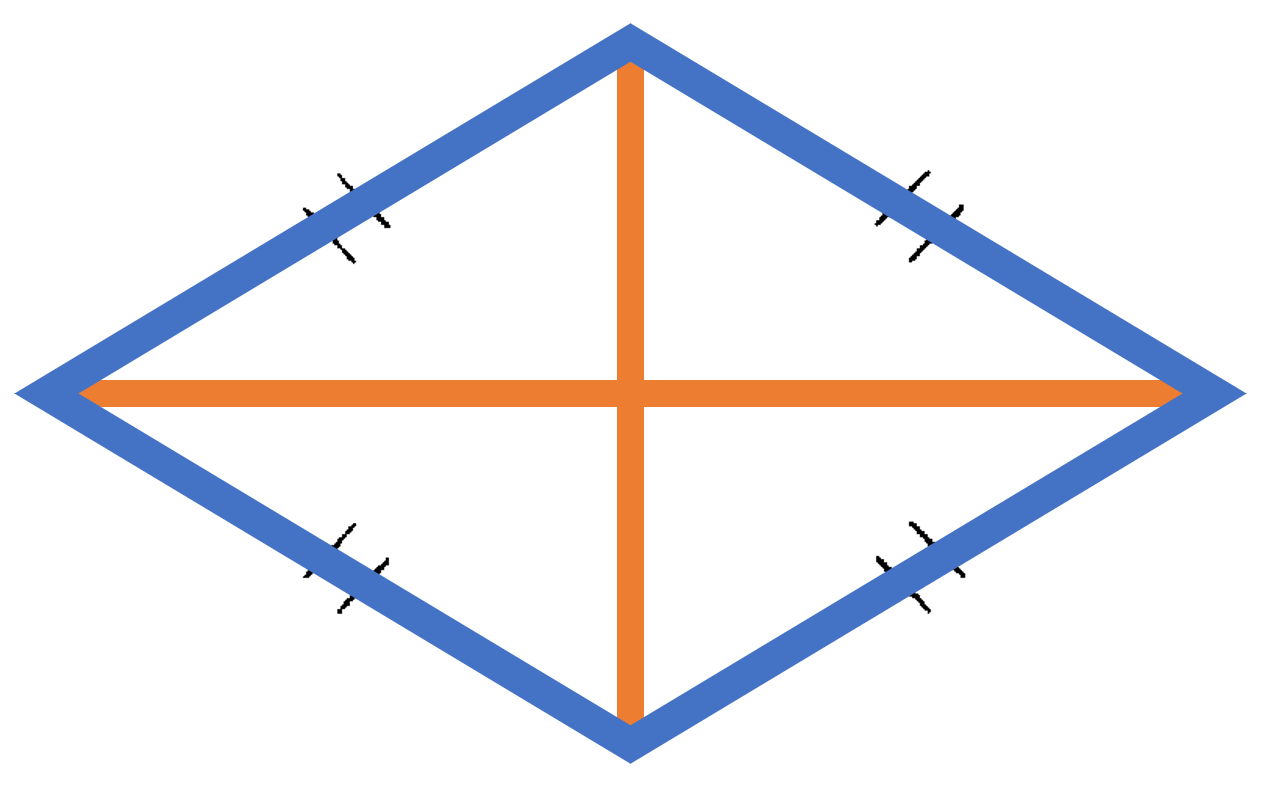
菱形:4つの辺が等しい四角形。
(1) 菱形は平行四辺形の特別な例(つまり菱形も平行四辺形)。
(2) 対角線が垂直に交わる。
正方形:4つの角が等しく4つの辺が等しい四角形。
(1) 長方形と菱形の性質をもつ。
(2) 対角線が互いに垂直で長さが等しい。
平行線と面積
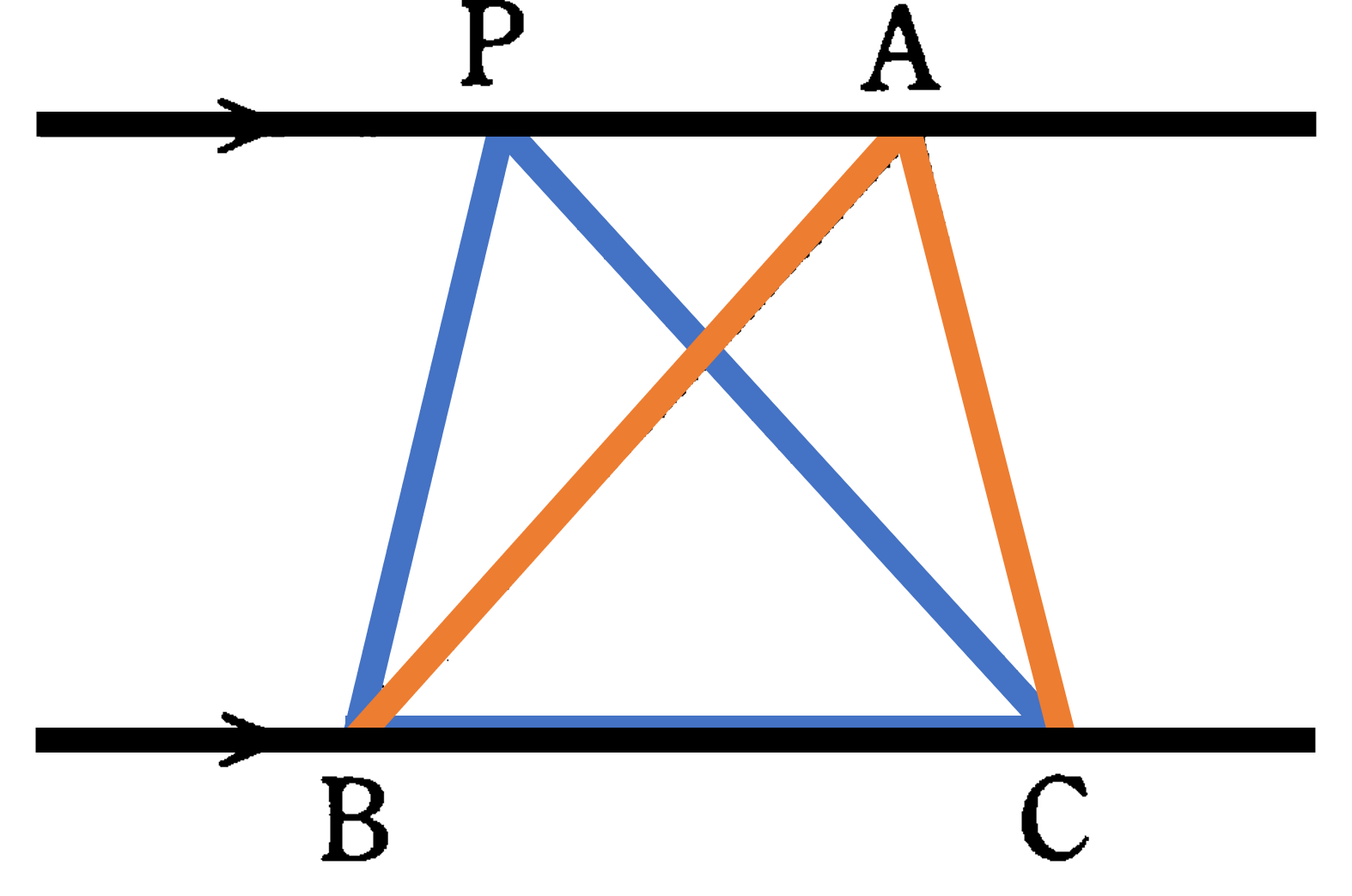
本節では、多角形の面積を変えずに平行線の性質を利用して変形する方法を考えてみましょう。下図のような、底辺 ${\rm BC}$ を共有し ${\rm BC}$ に平行な直線 $\ell$ 上に頂点を持つ ${\rm \triangle{ABC}}$, ${\rm \triangle{A’BC}}$, ${\rm \triangle{A^{\prime \prime}BC}}$ の面積を考えると、これらの三角形はみな、底辺が同じで高さが等しいため、面積が同じになります。このように、平行線を利用して、面積を変えずに図形を変形することができます。この変形を習得することで、一見計算できないような図形の面積を簡単に求めることができることがあります。演習重ねて、平行線と面積について、正しく理解しておきましょう。
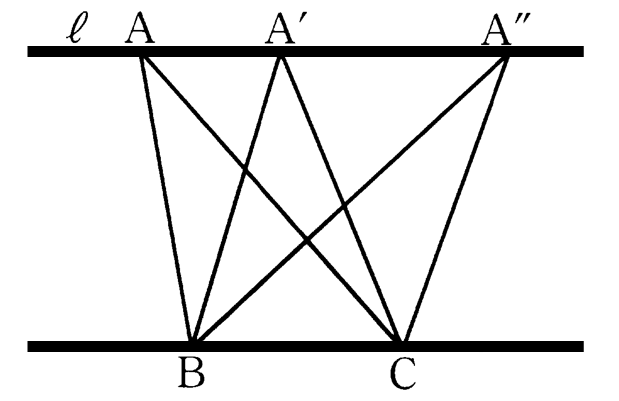
面積が等しい三角形:辺 ${\rm BC}$ を共有する ${\rm \triangle{PBC}}$ と ${\rm \triangle{ABC}}$ において
${\rm PA / \! \! / BC}$$\iff$${\rm \triangle{PBC}=\triangle{ABC}}$