🔄 最終更新日 2019年12月11日 by takara_semi
中1 > 4章:比例と反比例
たとえば1000枚を超える紙束の枚数を数えようと思うと大変です。そこで、枚数を直接数える代わりに紙1枚の重さを調べてから、紙束の重さを量れば、比例の関係から紙束の枚数を求めることができます。このように求めたい数量と関係のある数量をみつけて、その関係を利用することがとても便利な場合があります。本章では、このような便利な比例・反比例の関係を調べたり利用したりする方法を学びましょう。
比例
比例の関係を利用すれば、お店のレジの待ち時間や、家のお風呂のお湯がいっぱいになるまでの時間、出かける時に目的地に着く時間などを予測できるようになります。未来を予測できるようになるのです。ともなって変わる2つの数量の間に成り立つ関係について考え理解を深め、比例の関係の利用方法を習得しましょう。
変数:いろいろな値をとる文字。主に $x$, $y$, $z$ が変数として利用される。
関数:2つの変数 $x$, $y$ があり変数 $x$ の値を決めるとそれにともなって変数 $y$ の値が定まる時 $y$ は $x$ の関数であるという。
変域:変数の取り得る値の範囲。
例
変数 $x$ の取り得る値の範囲が $0$ 以上$5$ 未満のとき $x$ の変域は不等号を使って $0≦x<5$ と表すことができる。
※ 変域を数直線上で表現する場合:端の数を含む場合は ● 含まない場合は ○ を使って表すことが多い。つまり端の数を含む $≧, ≦$ の記号の場合は ● 端の数を含まない $>, <$ の記号の場合は ○ を使って表す。
比例を表す式:$y$ は $x$ に比例 $\to$ $y=ax$ ($a$ は定数で $a \neq 0$) また比例の式の中の文字 $a$ は定数であり比例定数という。
例
縦が $5$cm 横が $x$cm の長方形の面積を $y$${\rm cm^2}$とする。このとき $y$ を $x$ の式で表すと $y=5x$ となる。このとき比例定数は $5$ となる。
座標・比例のグラフ
本節では比例の式 $y=ax$ をグラフとして表現する方法を学びます。グラフの上での点の位置を $x$ と $y$ の値の組 $(x,y)$ で表す方法を理解することは、関数を図を用いて理解するための基礎知識となります。演習を繰り返してグラフでの表現方法と読み取り方法を正しく理解しましょう。
座標:横の直線を $x$ 軸または横軸、縦の直線を $y$ 軸または縦軸、 $x$ 軸 $y$ 軸を合わせて座標軸、座標軸の交点 $O$ を原点という。原点は平面においては $(x,y)=(0,0)$ である。また任意の点 ${\rm P}$ の位置を表すためには ${\rm P}(m,n)$ と書く。このとき $m$ を点 ${\rm P}$ の $x$ 座標 $n$ を点 ${\rm P}$ の $y$ 座標 $(m,n)$ を点 ${\rm P}$ の座標という。
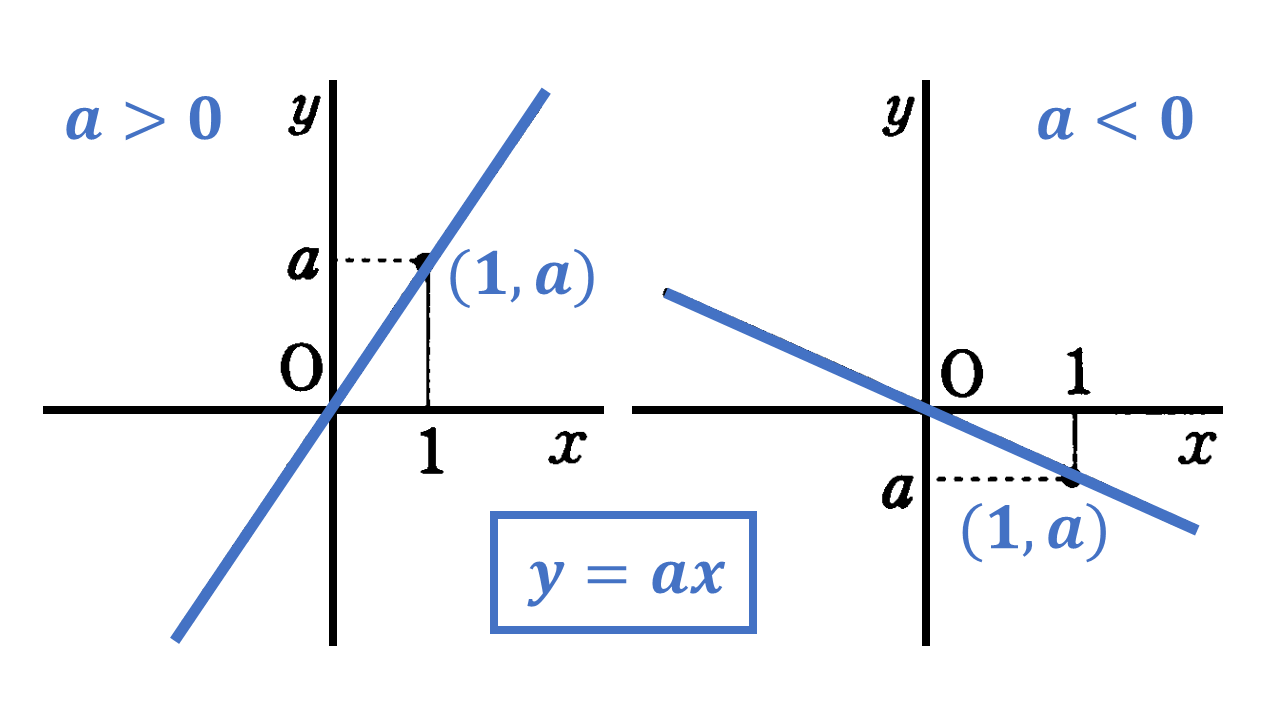
比例 $y=ax$ のグラフ:
(1) 原点 $(x,y)=(0,0)$ を通る直線。
(2) 比例定数が $a>0$ のとき $\to$ 右上がり。
(3) 比例定数が $a<0$ のとき $\to$ 右下がり。
(4) 描き方:原点と他の1点 $(x,y)=(m,n)$ を求めて直線で結ぶ。$x \neq 0$ のとき $\frac{y}{x}=\frac{m}{n}=a$ の値は一定で比例定数 $a$ に等しいため比例の表やグラフが与えられれれば比例の式 $y=ax$ を求められる。また反対に比例の式 $y=ax$ が与えられれば比例の表やグラフを求めることができる。
反比例とそのグラフ
反比例する関係にはどのようなものがあるでしょうか。たとえば道のりが分かっているときに、歩く速さと必要な時間の間には反比例の関係が成り立ちます。距離が決まっている時、速く歩くと必要な時間が短くなるためです。他にも面積が決まっている長方形の縦横の長さの間にも反比例の関係が成り立ちます。このように一方が増加すると他方が減少する関係(トレードオフの関係)は世の中に無数に存在し、また非常に大切な考え方です。本節で正しく理解しておきましょう。
反比例:$y$ は $x$ に反比例 $\to$ $y=\frac{a}{x}$ ($a$は定数, $a \neq 0$, $x \neq 0$) ここで定数 $a$ は比例定数とよばれる(比例の関係の時と同様)。また反比例のグラフはなめらかな2つの曲線となり、この曲線を双曲線という。この $y=\frac{a}{x}$ のグラフは $x$ 軸および $y$ 軸とは交わらない(軸を延長しても交わることはない)。
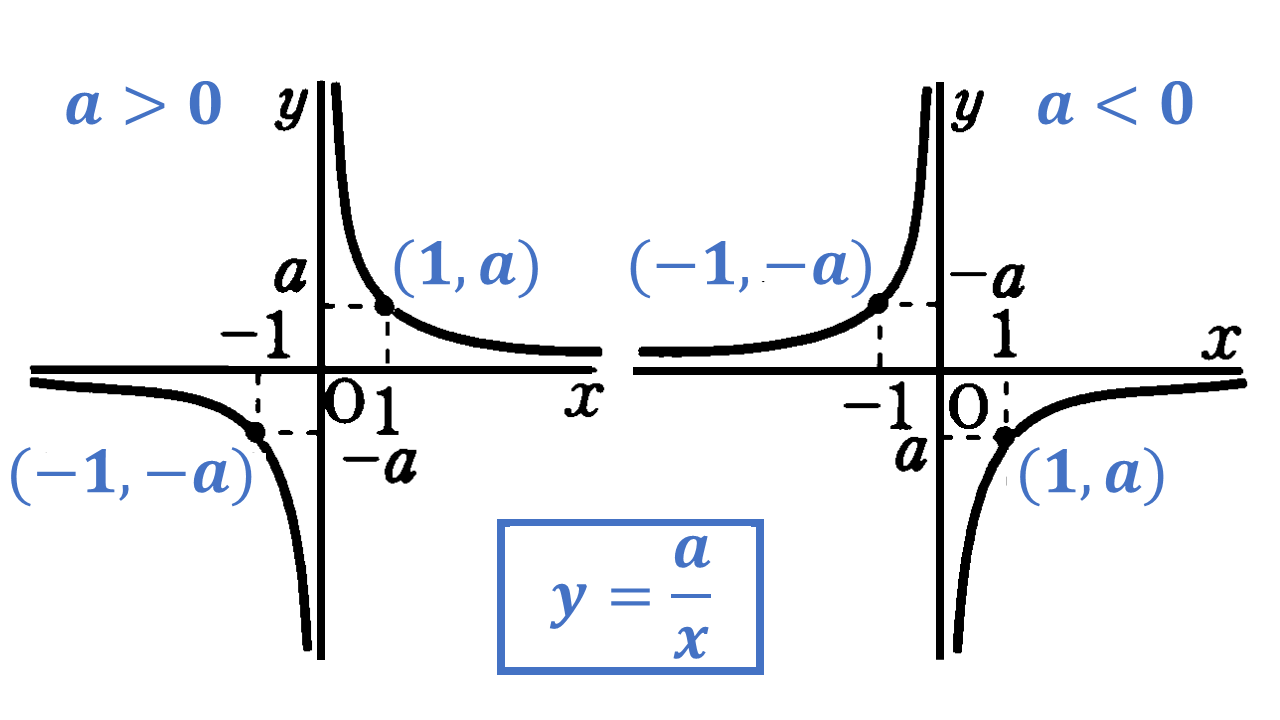
反比例のグラフ:
(1) 双曲線とよばれる曲線になる。
(2) 原点について点対称である。
(3) 比例定数 $a$ が $a>0$ のとき $\to$ $x$ が増加するとき $y$ は減少する。
(4) 比例定数 $a$ が $a<0$ のとき $\to$ $x$ が増加するとき $y$ も増加する。
(5) 描き方:点 $(x,y)=(m,n)$ が得られたとき $xy=mn=a$ の値は一定で比例定数 $a$ に等しいため反比例の表やグラフが与えられれれば反比例の式 $y=\frac{a}{x}$ を求められる。また反対に反比例の式 $y=\frac{a}{x}$ が与えられれば反比例の表やグラフを求めることができる。
比例と反比例の利用
身近な問題を比例や反比例の関係を利用して解決してみましょう。(1) 紙束の枚数を重さから計算したり (2) 決まった量の課題を制限時間内にグループで終わらすために必要な人数を求めたり (3) 地震の揺れを予測したり (4) 自転車の変速機の仕組みを調査したり…これまでに学んだ知識を活用して、自由に問題を解決してみましょう。
※ (1) は比例の関係:1枚の重さが$5$gだったとすると、紙束の枚数を $y$ 枚、重さを $x$gとすれば $y=\frac{x}{5}$ の関係式から紙束の枚数を計算できる。(2) は反比例の関係:課題が100ページの数学ドリルで、時間何に1人あたりが終わらすページ数を $x$ ページ、グループの人数を $y$ 人とすると $xy=100$ となり反比例の関係が得られ $y=\frac{100}{x}$ の関係式から必要な人数を計算できる。(3) は比例の関係:地震の揺れを伝える波(P波とS波)の伝達速度からどの場所でいつ地震が発生するかを予測することができる(緊急地震速報のシステムなど)。 (4) はギアの歯の数の比に注目して自由に考えてみましょう。
ともなって変わる3つの変数 $x,y,z$ があって関係 $z=xy$ が成り立つとき:
(1) $x$ が一定なら $z$ は $y$ に比例する( $z=ay$ ($a$ は定数))。$y$ が一定なら $z$ は $x$ に比例する( $z=ax$ ($a$ は定数))。
(2) $z$ が一定なら $y$ は $x$ に反比例する( $y=\frac{a}{x}$ ($a$は定数))。$x$は$y$に反比例する($x=\frac{a}{y}$ ($a$は定数))。

