🔄 最終更新日 2022年10月24日 by takara_semi
問題
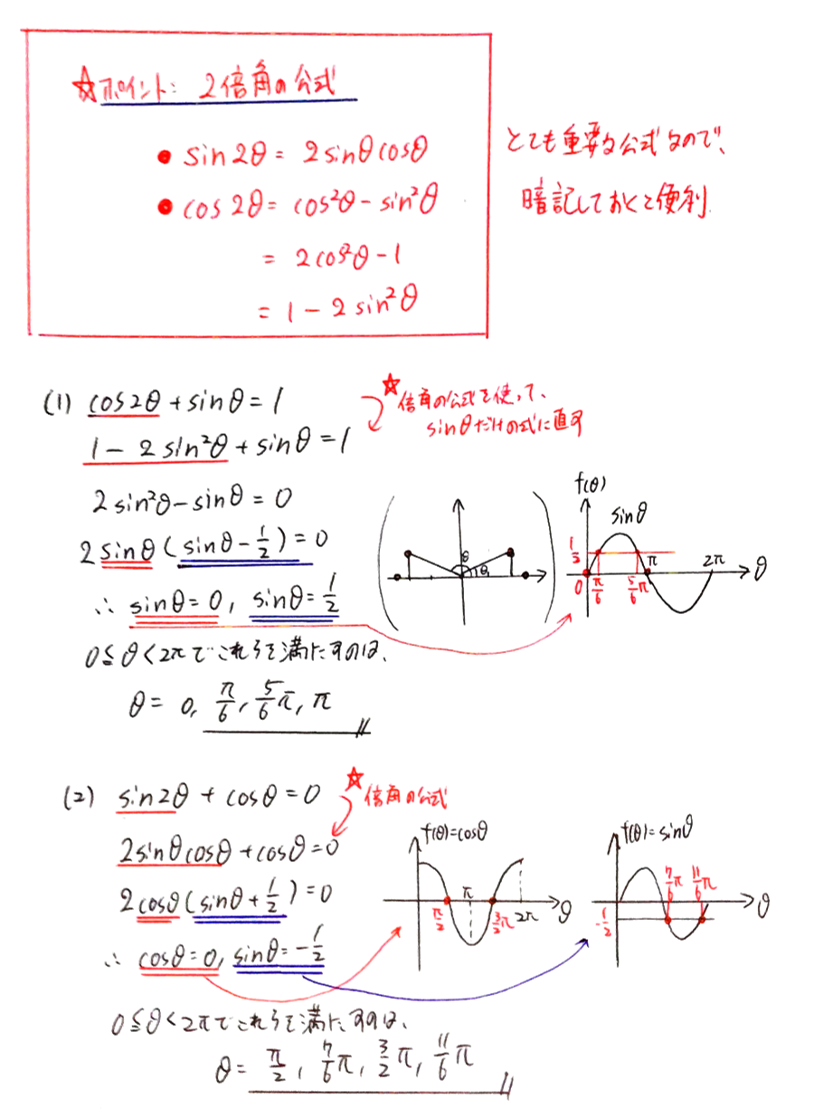
以下の方程式を解け.ただし $0≦\theta<2\pi$ とする.
(1) $\cos{2\theta}+\sin{\theta}=1$
(2) $\sin{2\theta}+\cos{\theta}=0$
以下の方程式を解け.ただし $0≦\theta<2\pi$ とする.
(1) $\cos{2\theta}+\sin{\theta}=1$
(2) $\sin{2\theta}+\cos{\theta}=0$

三角関数を含む方程式は,多少面倒であっても,簡単な図を描いて,正確に解を求めましょう.また2倍角の公式は加法定理より容易に導けるので,忘れてしまっても,導出できるよう確認しておきましょう.
検索キーワード:
三角関数, 方程式, 2倍角の公式, $0≦\theta<2\pi$, $\cos{2\theta}+\sin{\theta}=1$, $\sin{2\theta}+\cos{\theta}=0$.