🔄 最終更新日 2019年12月11日 by takara_semi
中3 > 7章:三平方の定理
本章では、三平方の定理について学びます。三平方の定理はピタゴラスの定理ともいい、非常に便利で実用的な定理です。その証明方法や活用方法について学び、いろいろな問題に対して、この定理を利用できるようになりましょう。
三平方の定理
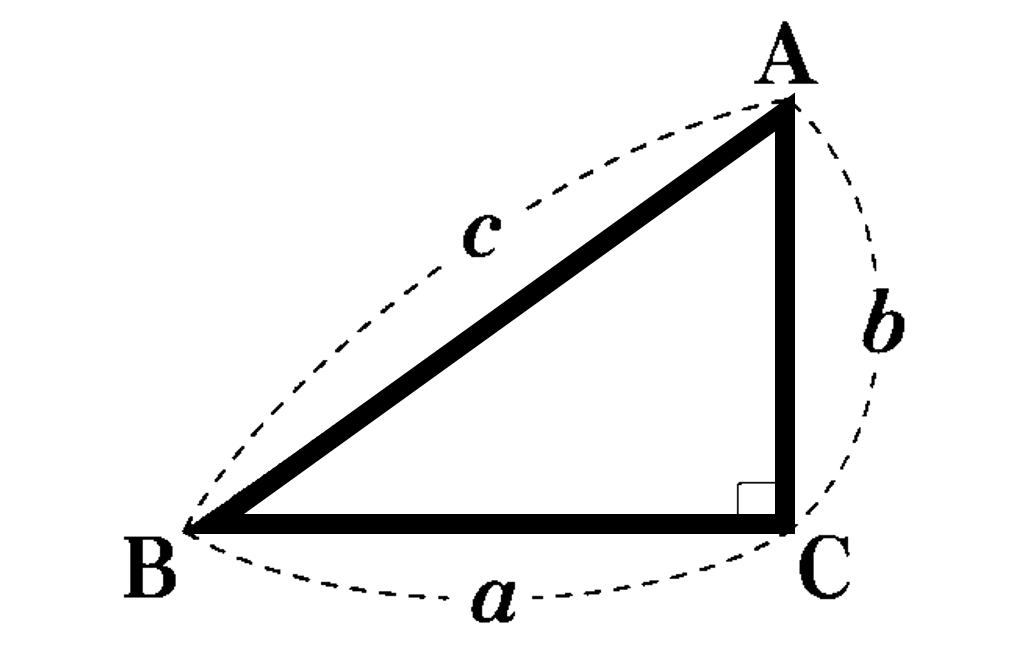
三平方の定理とは「直角三角形の直角をはさむ2辺の長さを $a,b$ 斜辺の長さを $c$ としたときに $a^2+b^2=c^2$ という関係が成り立つ」というものです。この定理は、古代エジプト時代から知られており、ギリシャの数学者であるピタゴラスにちなんでピタゴラスの定理ともよばれます。
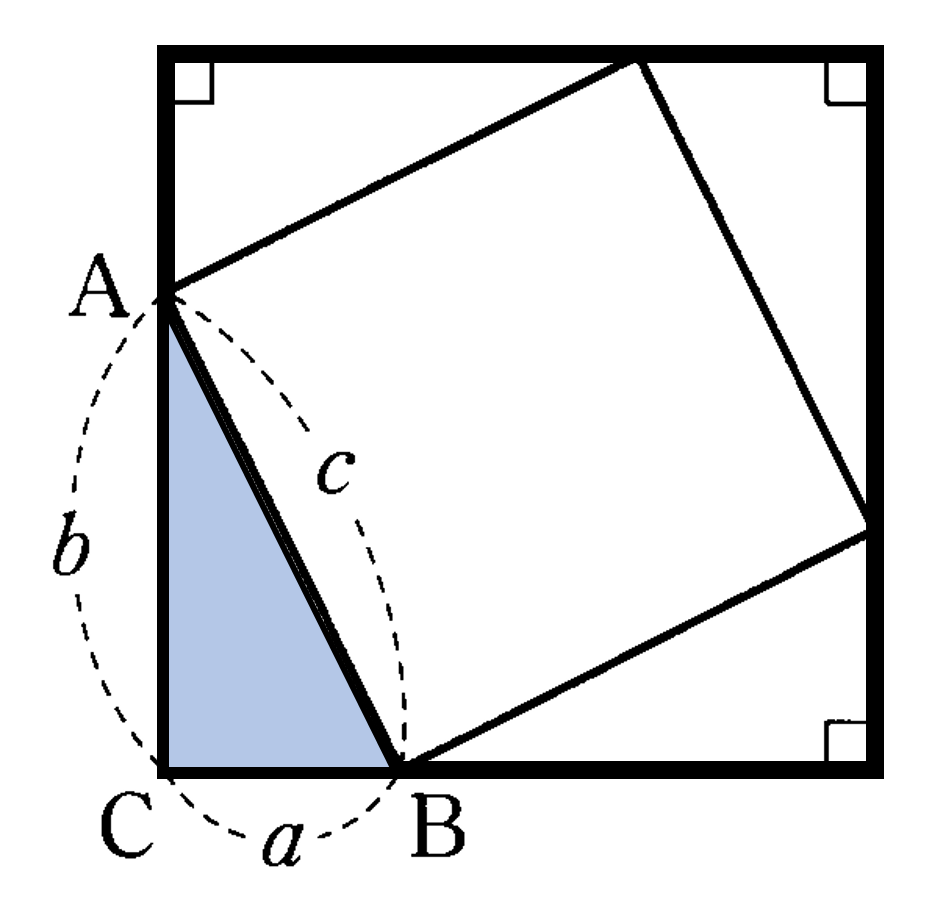
下の図のように、直角三角形 $\triangle {\rm ACB}$ と合同な直角三角形を、1辺の長さが $c$ の正方形の周りに描きます。そうすると、外側に1辺が
の長さが $a+b$ の正方形ができます。この図で面積の関係を考えます。(1辺 $c$ の正方形の面積)$=$(1辺 $a+b$ の正方形の面積)$-$($\triangle {\rm ABC}$ の面積)$\times 4$ であるから
\begin{eqnarray}
c^2 &=& (a+b)^2-\frac{1}{2}ab \times 4 \\
&=& (a^2+2ab+b^2)-2ab \\
&=& a^2+b^2
\end{eqnarray}
よって三平方の定理が証明されました。
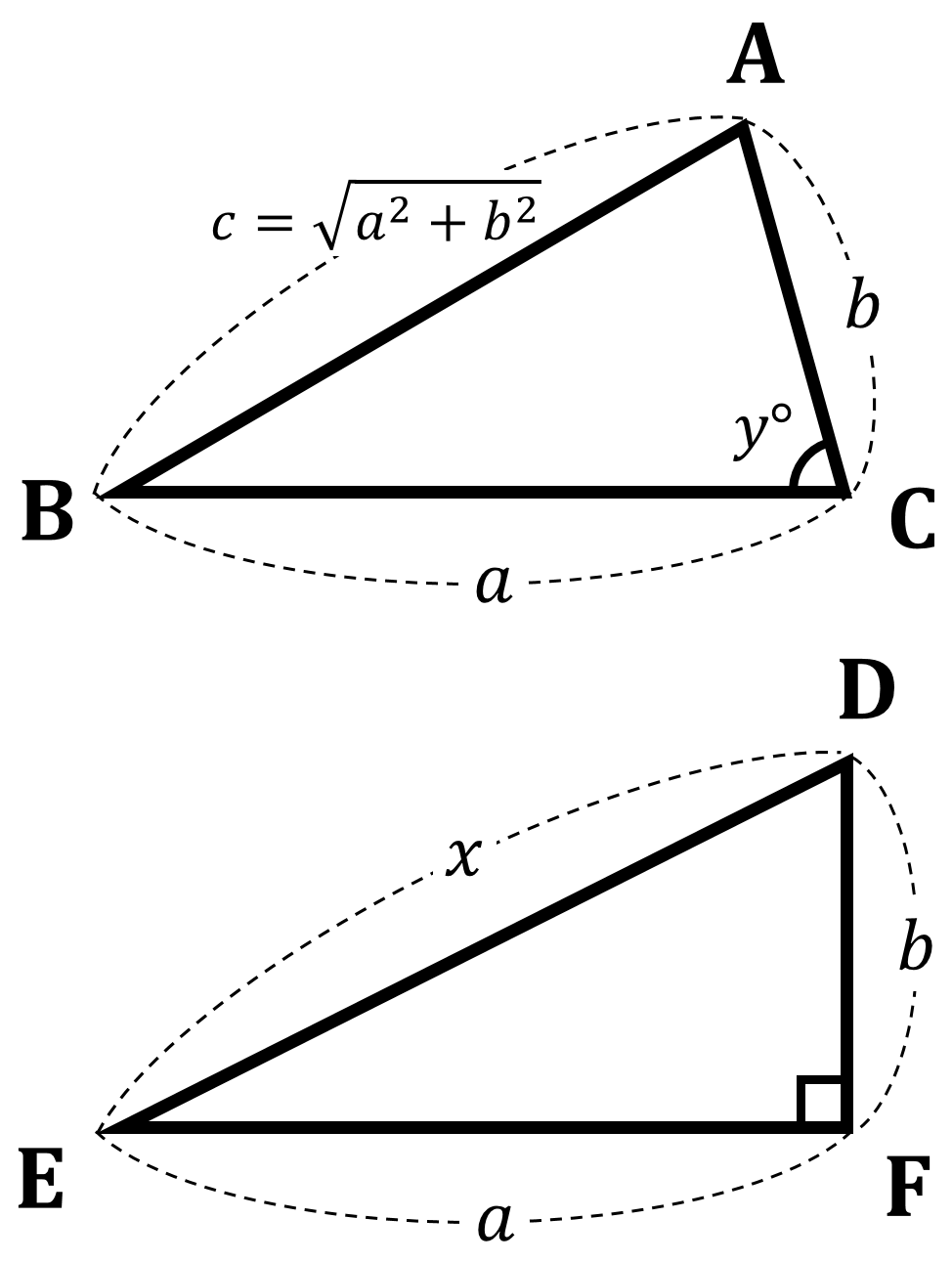
下の図のように ${\rm BC} = a$,${\rm CA} = b$,${\rm AB} = c$ で $a^2+b^2=c^2$ が成り立つ $\triangle {\rm ABC}$ を考えます。この三角形の斜辺に対する角 $\angle {\rm C} = y$ とします。次に ${\rm EF} = a$,${\rm FD} = b$,${\rm DE} = x$, $\angle {\rm F} = 90^{\circ}$ である $\triangle {\rm DEF}$ を考え $\triangle {\rm ABC}$ と比較します。
$\triangle {\rm DEF}$ において三平方の定理より
$a^2+b^2=x^2$・・・①
仮定から
$a^2+b^2=c^2$・・・②
①②より
$x^2=c^2$
$x > 0$,$c > 0$であるから
$x=c$
つまり
${\rm DE} = {\rm AB}$・・・③
仮定より
${\rm EF} = {\rm BC}$・・・④
${\rm FD} = {\rm CA}$・・・⑤
③④⑤より
$\triangle {\rm ABC}$ と $\triangle {\rm DEF}$ において3組の辺がそれぞれ等しいため
$\triangle {\rm ABC} ≡ \triangle {\rm DEF}$
したがって対応する角の大きさは等しいので
$\angle {\rm C} = \angle {\rm F}$
$y=90^{\circ}$
よって三平方の定理の逆が成り立つことが証明できました。
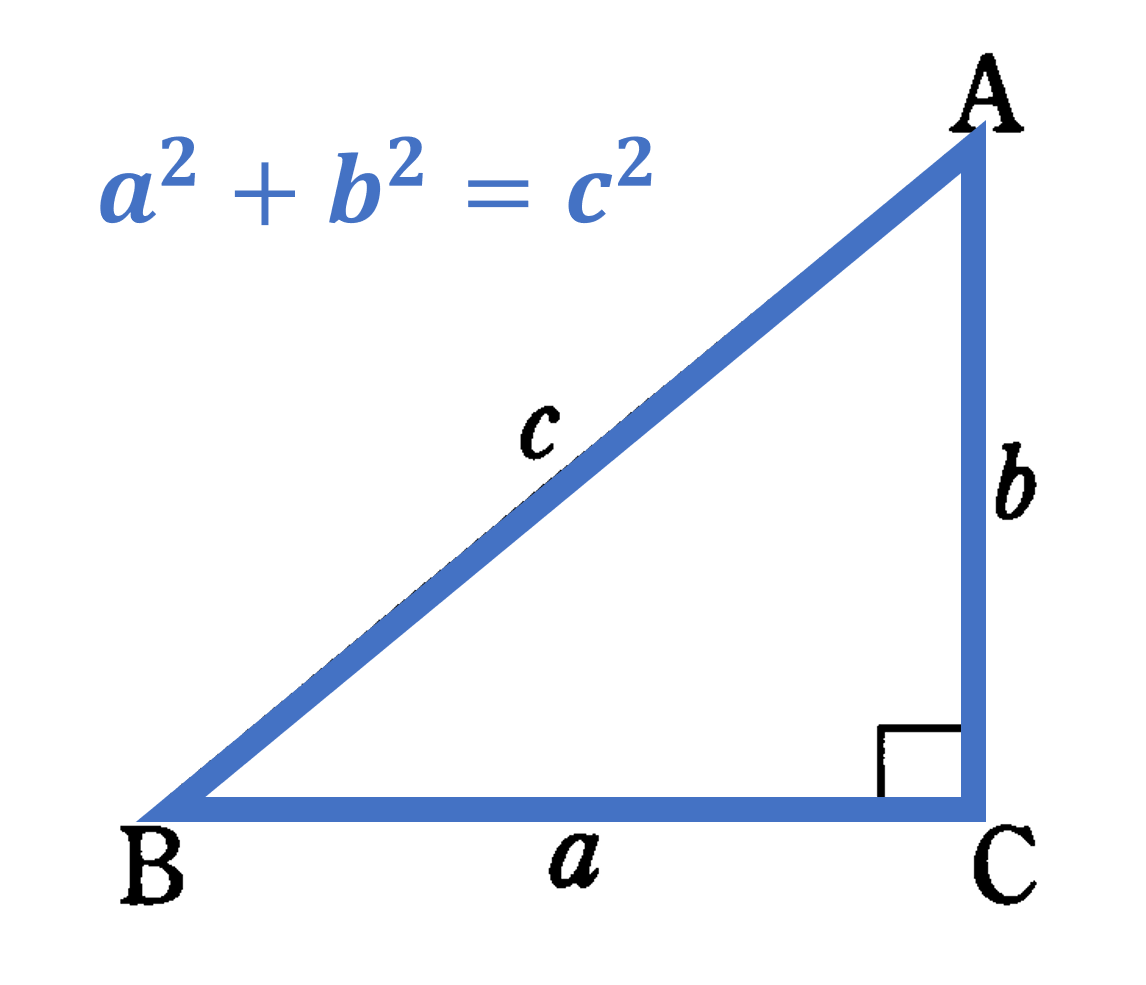
三平方の定理:直角三角形の直角をはさむ2辺の長さを $a$, $b$ 斜辺の長さを $c$ とすると $a^2+b^2=c^2$ が成り立つ。
数学が面白くなる動画―17
三平方の定理の証明方法を考えてみましょう。
3辺の長さが $a,b,c$ である三角形において $a^2+b^2=c^2$ が成り立つならばその三角形は長さ $c$ の辺を斜辺とする直角三角形である。
三平方の定理の利用
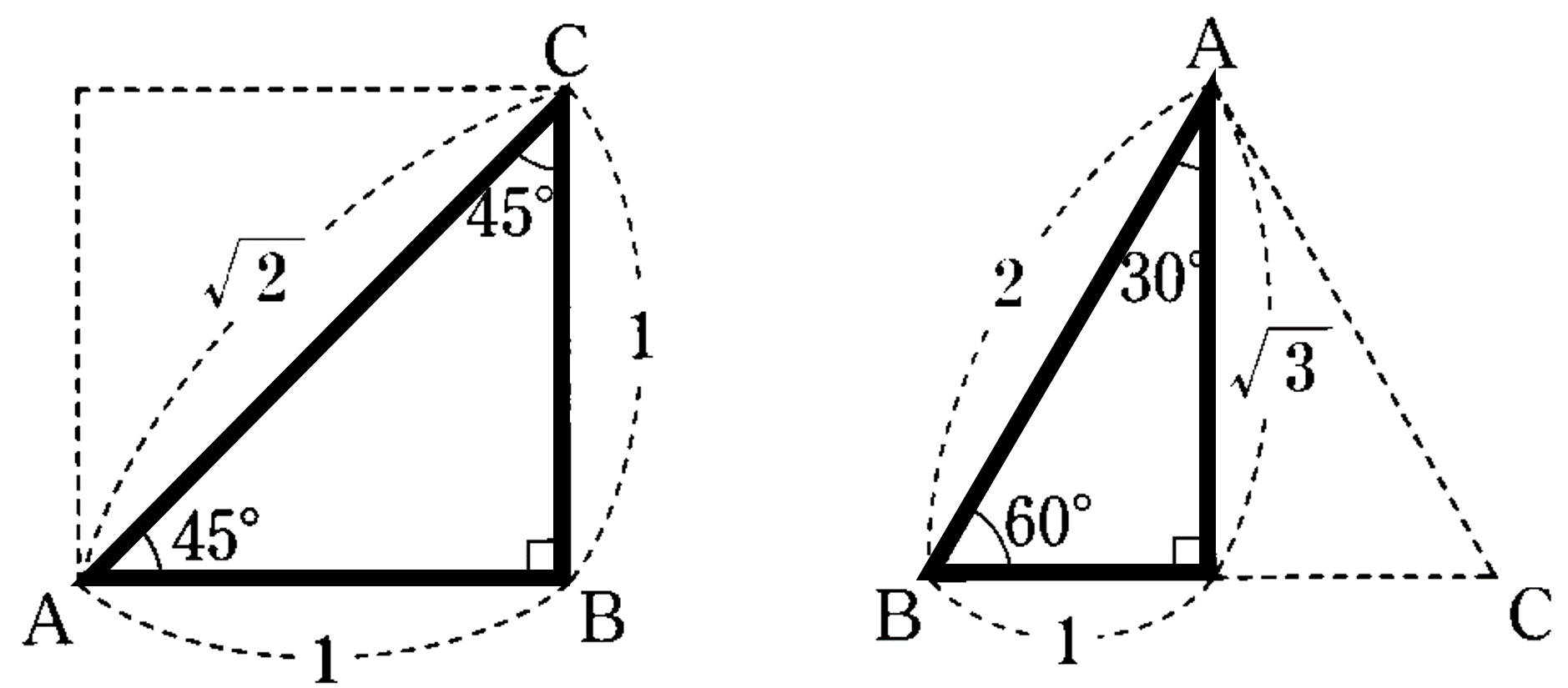
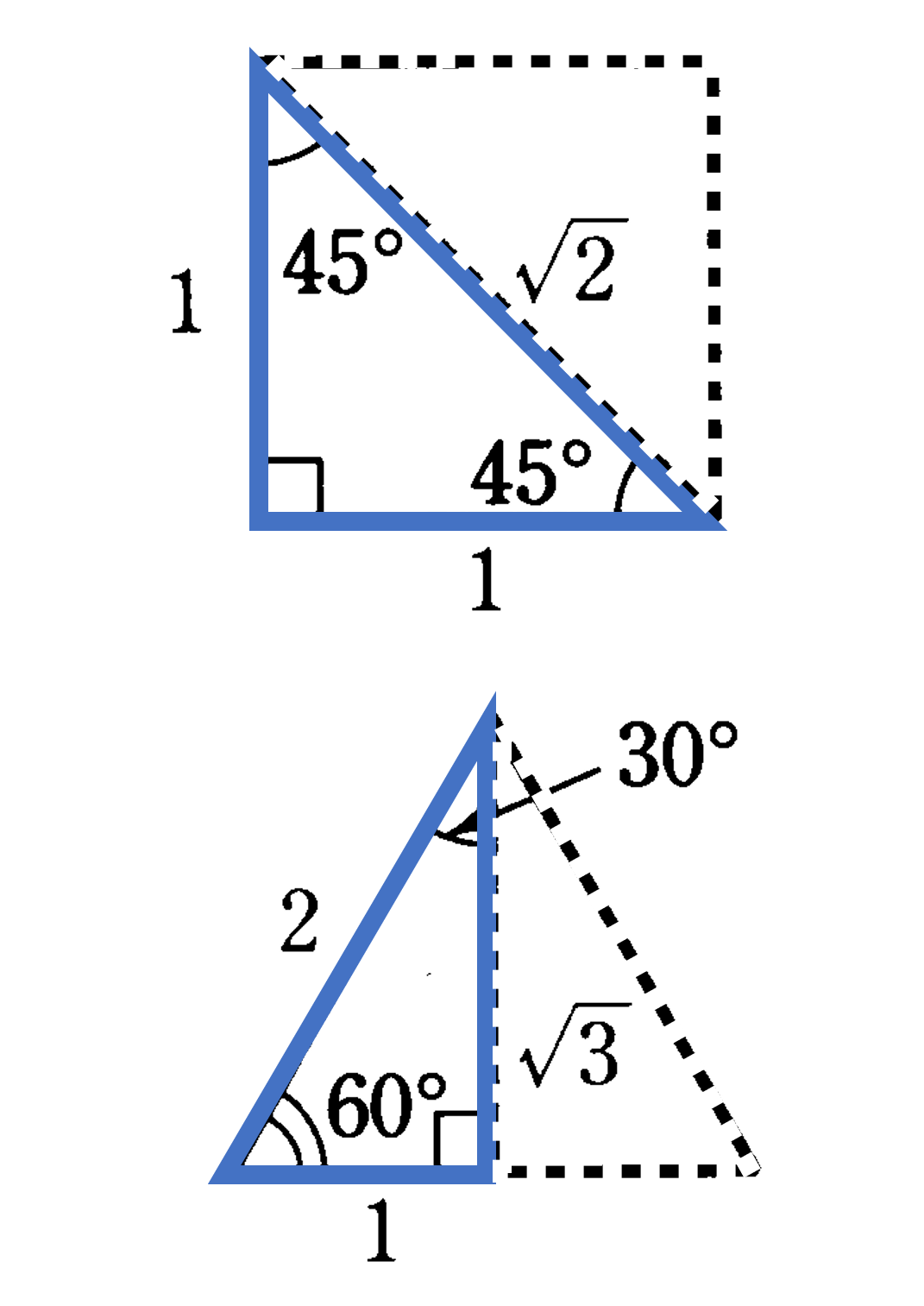
本節では、三平方の定理を利用して、いろいろな長さを求める方法について考えてみましょう。例えば特徴的な直角三角形として、3つの角が$45^{\circ}$, $45^{\circ}$, $90^{\circ}$ である直角三角形と $30^{\circ}$, $60^{\circ}$, $90^{\circ}$ である直角三角形の3辺の長さは、下図のような関係が成り立っています。この関係は非常に重要で、問題にもよく利用されますので、正しく理解しておきましょう。
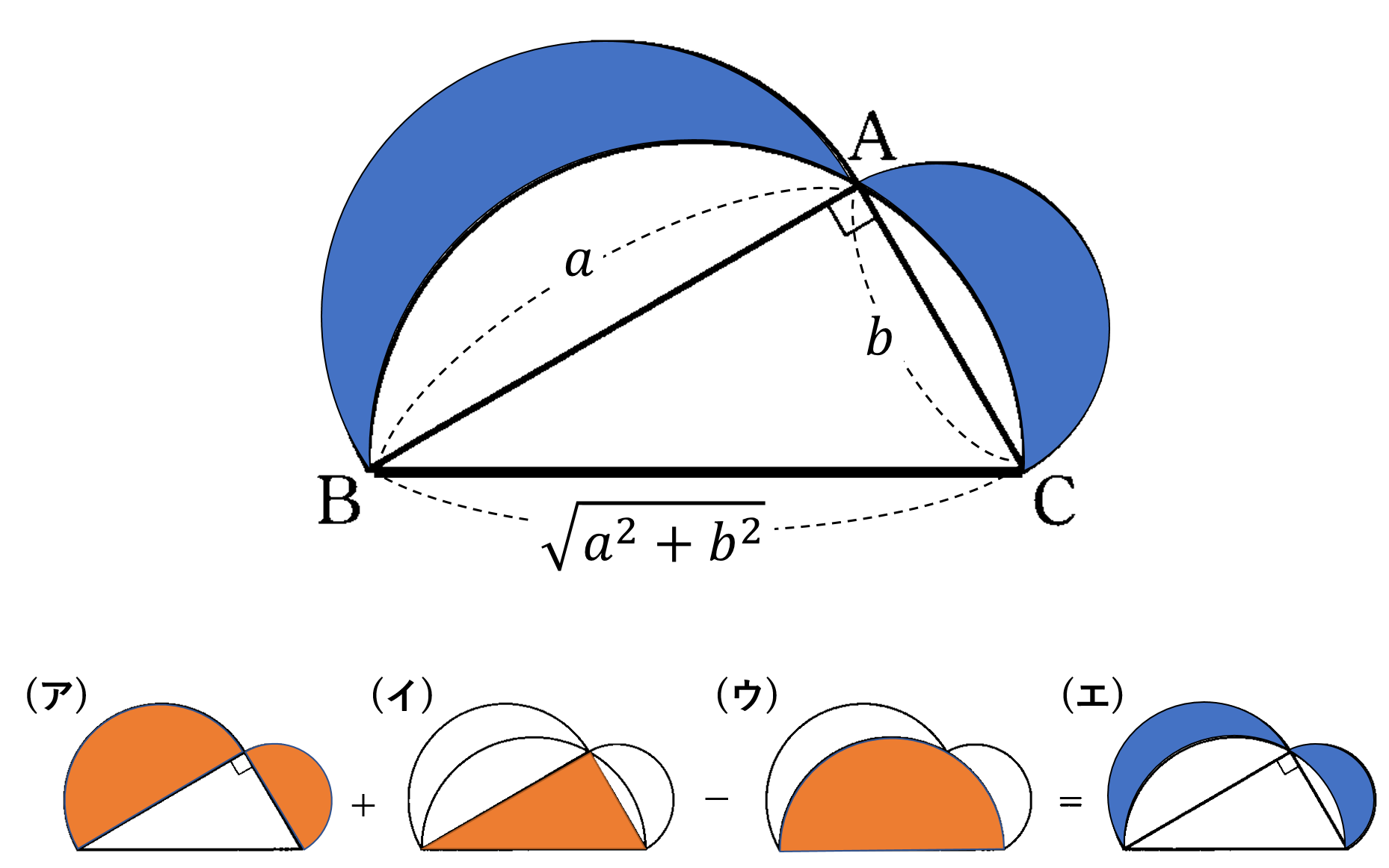
ヒポクラテスの月形の面積(エ)は、下の図のように(ア)$+$(イ)$-$(ウ)という計算で求めることができます。
\begin{eqnarray}
(ア)&=&\pi a^2 \times \frac{1}{2}+\pi b^2 \times \frac{1}{2}\\
&=&\frac{1}{2}\pi(a^2+b^2) ・・・①\\
\\
(イ)&=&\frac{1}{2}ab ・・・②
\\
(ウ)&=&\pi (\sqrt{a^2+b^2})^2 \times \frac{1}{2}\\
&=&\frac{1}{2}\pi(a^2+b^2) ・・・③
\end{eqnarray}
①②③より
\begin{eqnarray}
(エ)&=&(ア)+(イ)-(ウ)\\
&=&\frac{1}{2}\pi(a^2+b^2)+\frac{1}{2}ab\\
& &-\frac{1}{2}\pi(a^2+b^2)\\
&=&\frac{1}{2}ab
\end{eqnarray}
となり、ヒポクラテスの月形の面積は、直角三角形 $\triangle {\rm ABC}$ の面積と等しくなることが分かります。
このように、三平方の定理を学ぶことで、一見複雑な図形の面積も求めることができるようになります。応用範囲の広い「三平方の定理」を是非、正しく理解しておきましょう。
特別な直角三角形の3辺の長さの比:
(1) 直角二等辺三角形 $\to$ $1:1:\sqrt{2}$
(2) $30^{\circ},60^{\circ}$ の直角三角形 $\to$ $1:2:\sqrt{3}$
2点 ${\rm A},{\rm B}$ 間の距離は ${\rm AB}$$=\sqrt{(x\small{座標の差})^2+(y\small{座標の差})^2}$
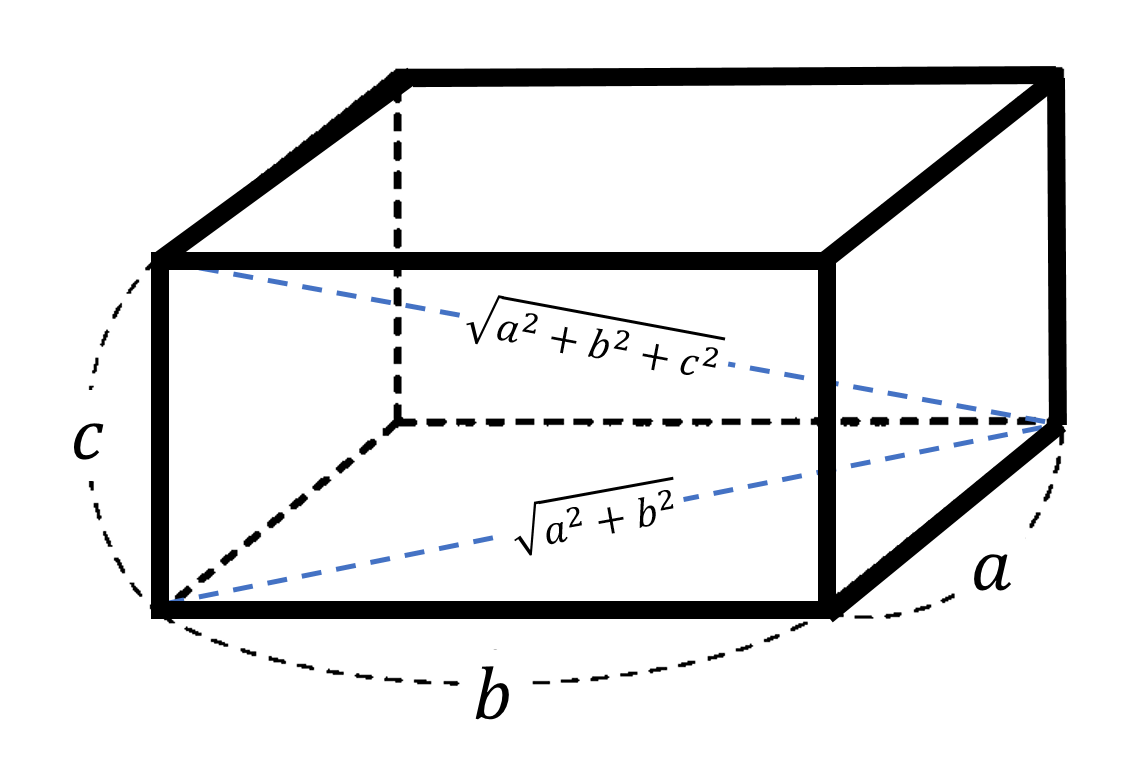
直方体の対角線の長さ:
縦 $a$ 横 $b$ 高さ $c$ の直方体の対角線の長さを $\ell$ とすると $\ell=\sqrt{a^2+b^2+c^2}$

