🔄 最終更新日 2019年12月11日 by takara_semi
中3 > 6章:円
本章では、円の性質について詳しく調べます。円は1点からの距離が一定である点の集まりであり、たとえば円周上に頂点を持つ角には特別な性質がみられます。このような、円についての様々な性質を調査し、その活用方法や見方を広げていきましょう。
円周角の定理
本節では、円周角の定理について学習します。円 ${\rm O}$ において弧 $\stackrel{\frown}{\rm AB}$ をのぞく円周上の点を $P$ とするとき $\angle {\rm APB}$ を「弧 $\stackrel{\frown}{\rm AB}$ に対する円周角」といいます。また、弧 $\stackrel{\frown}{\rm AB}$ を「円周角 $\angle {\rm APB}$ に対する弧」といいます。
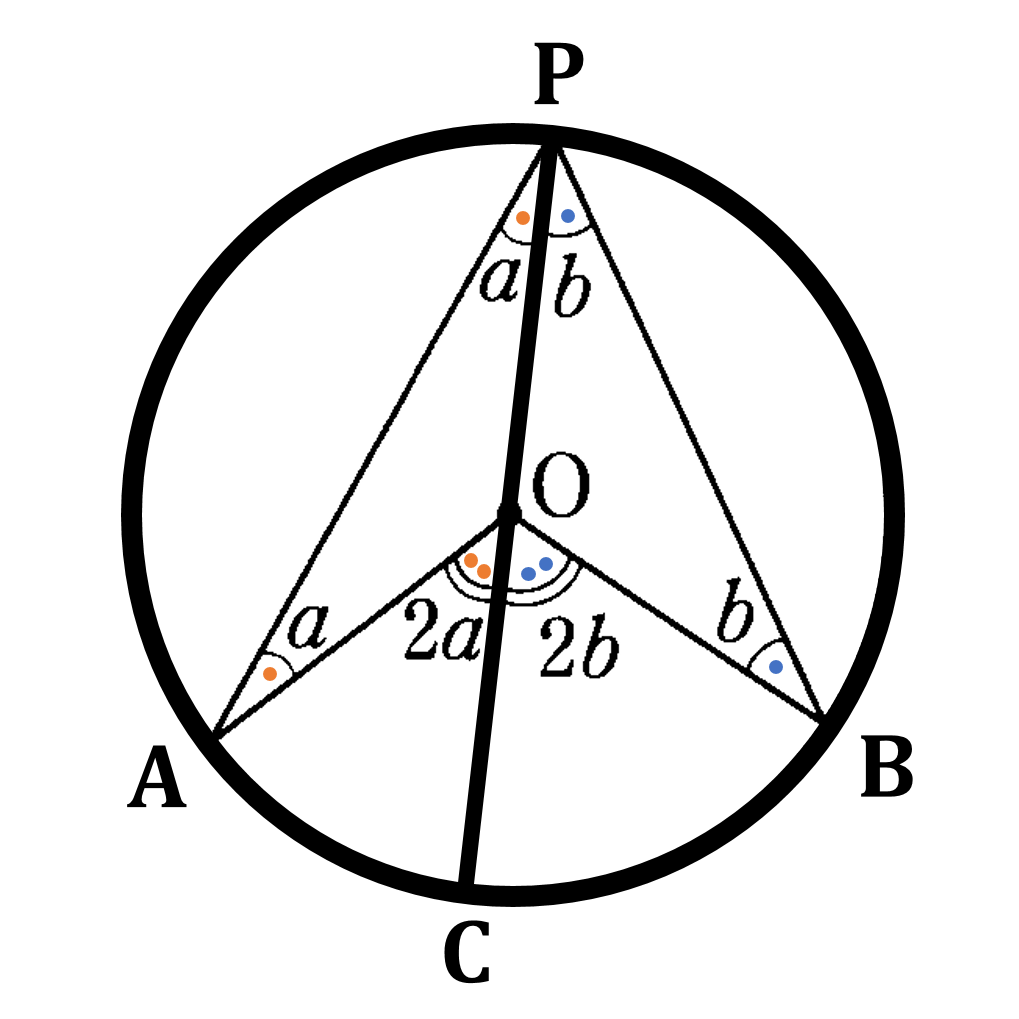
続いて円周角の定理についてみていきましょう。円周角の定理とは「1つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の半分である」というものです。この定理の証明をしましょう。
下の図において直径 ${\rm PC}$ をひき $\angle {\rm OPA}=\angle a$, $\angle {\rm OPB}=\angle b$ とします。
${\rm OP=OA}$ であるから
$\angle {\rm OAP}=\angle a$
$\angle {\rm AOC}$ は ${\rm \triangle{OPA}}$ の外角なので
$\angle {\rm AOC}$$=\angle {\rm OAP}+\angle {\rm OPA}$$=2\angle a$
同様にして
$\angle {\rm BOC}$$=2\angle b$
したがって
$\angle {\rm AOB}$$=2(\angle a + \angle b)$
また
$\angle {\rm APB}$$=\angle a + \angle b$
であるから
$\angle {\rm APB}$$=\frac{1}{2}\angle {\rm AOB}$
弧 $\stackrel{\frown}{\rm AB}$ に対する中心角 $\angle {\rm AOB}$ は1つに定まるため、$\angle {\rm APB}$ の大きさは $\frac{1}{2}\angle {\rm AOB}$ で一定となる。(証明終了)
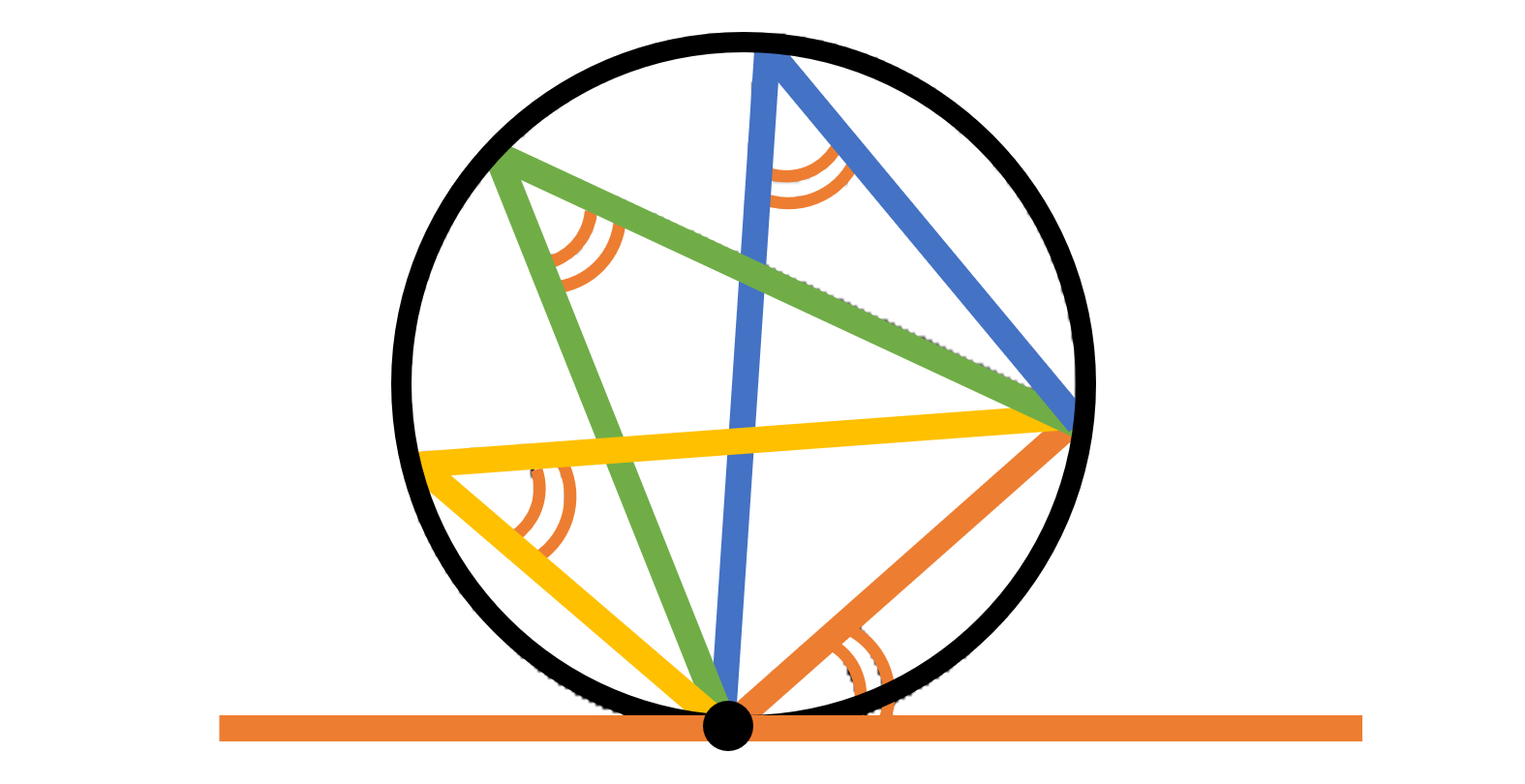
続いて、円周角と弧の性質について、より詳細にみていきましょう。例えば、1つの円で「等しい中心角に対する弧は等しく」なります。逆に「等しい弧に対する中心角も等しく」なります。これらの性質と中心角の定理から、1つの円において「等しい円周角に対する弧は等しく」なり「等しい弧に対する円周角も等しく」なります。また1つの円で「等しい弧に対する弦も等しく」なります。しかしながら、1つの弦に対する弧は2つ存在するため「等しい弦に対する弧は等しい」とはいえないので注意が必要です。
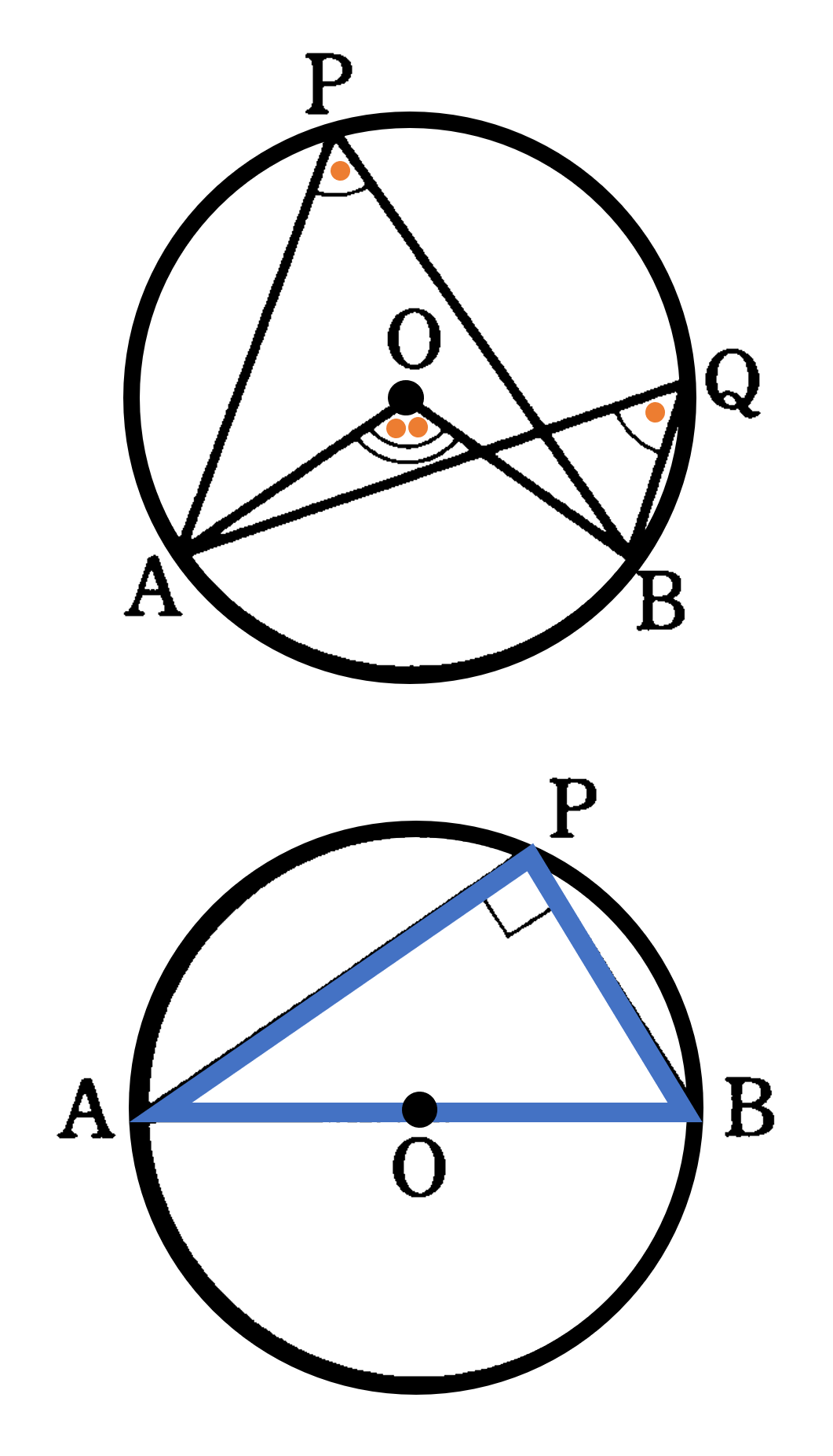
また、直径と円周角の間にも特別な性質があります。半円の弧に対する中心角が $180^{\circ}$ となることから、その円周角は $90^{\circ}$ となります。つまり、線分 ${\rm AB}$ を直径とする円の円周上に、点 ${\rm A,B}$ と異なる点 ${\rm P}$ をとれば $\angle {\rm APB}=90^{\circ}$(直角)となります。この性質の逆も成り立ち、円周上の3点 ${\rm A,P,B}$ について $\angle {\rm APB}=90^{\circ}$(直角)であるならば、線分 ${\rm AB}$ は円の直径になります。
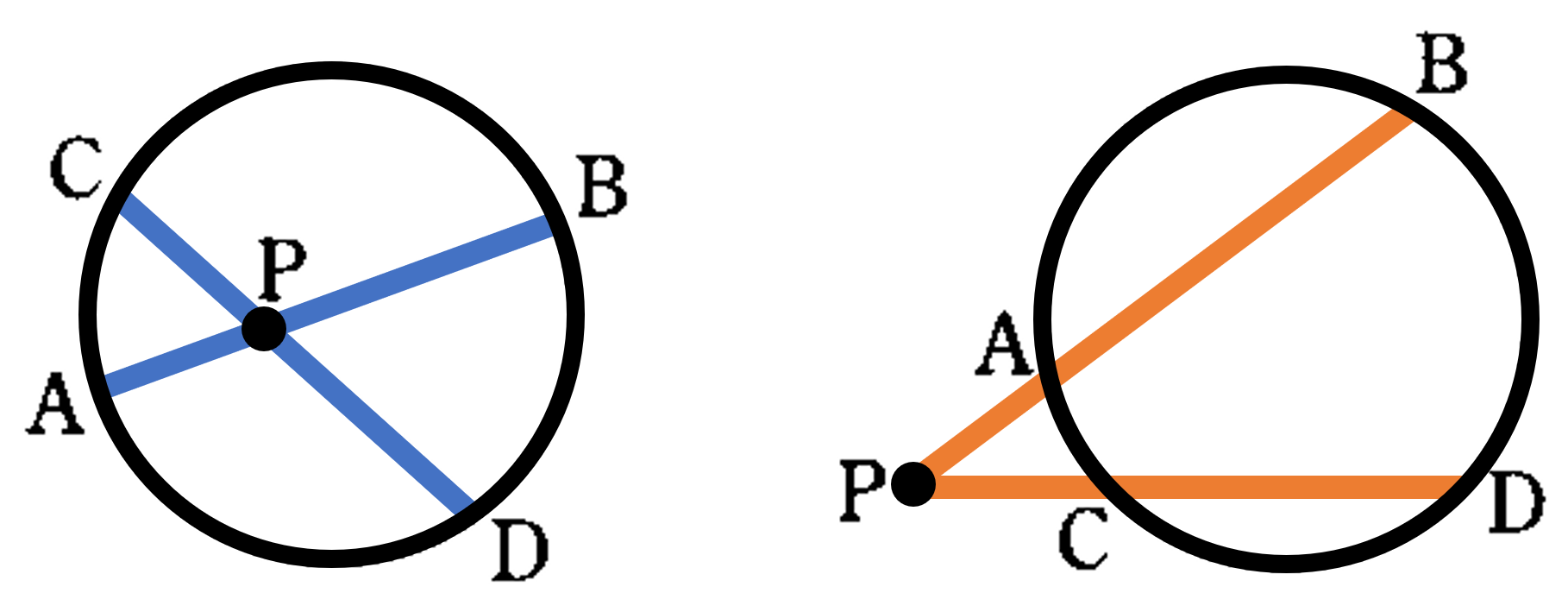
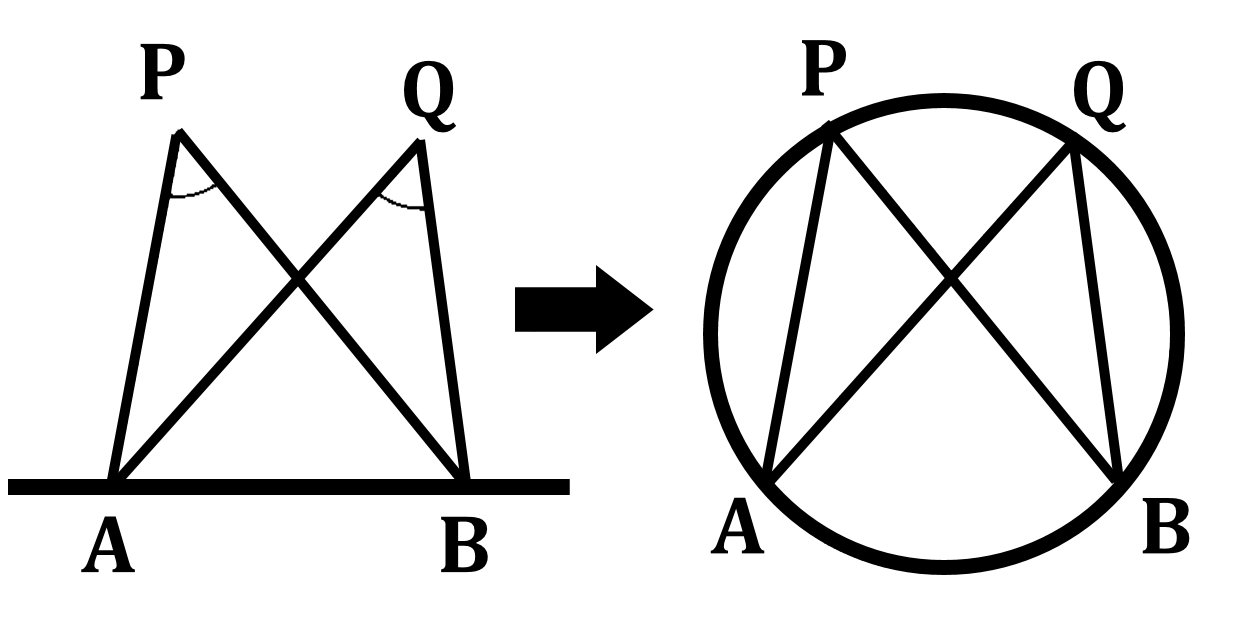
最後に、円周角の定理の逆について考えてみましょう。円周角の定理の逆は、下の図において「4点 ${\rm A,B,P,Q}$ について点 ${\rm P,Q}$ が直線 ${\rm AB}$ の同じ側にあり $\angle {\rm APB}=\angle {\rm AQB}$ ならば、この4点は1つの円周上にある」という性質になります。以下に、この性質が成り立つことを簡単に説明します。
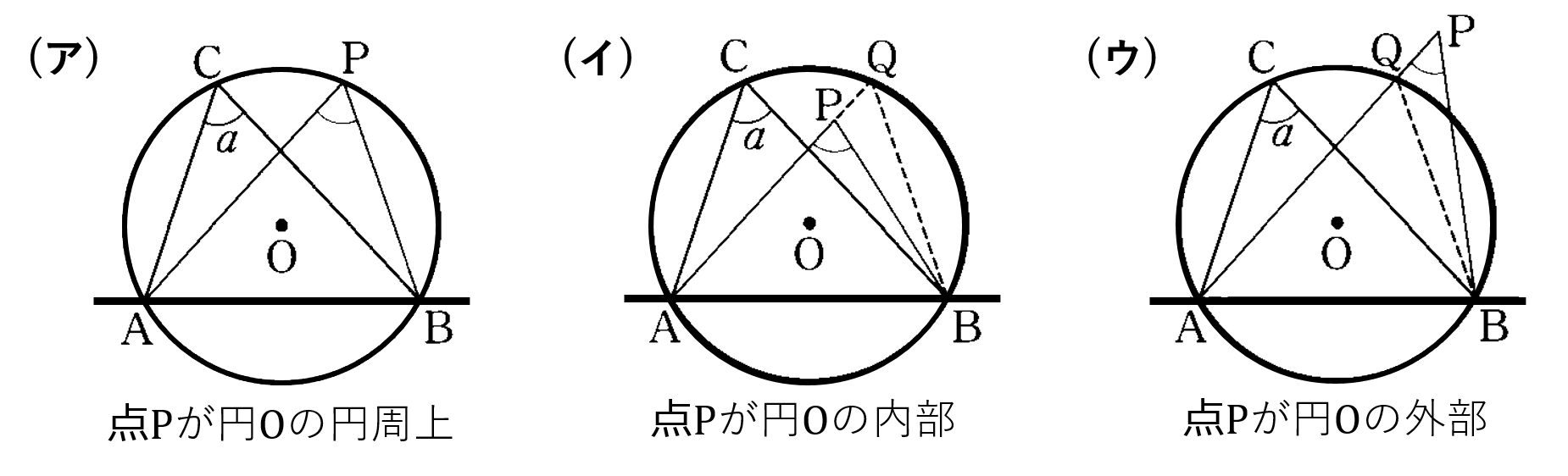
下の図のように、点 ${\rm P}$ が円 ${\rm O}$ の円周上や内部、外部にあるときの $\angle {\rm APB}$ と $\angle a$ の大きさを比べます。
(ア) 円周上にある場合
円周角の定理より
$\angle {\rm APB}=\angle a$・・・①
(イ) 内部にある場合
${\rm AP}$ の延長線と円周との交点を ${\rm Q}$ とすると $\angle {\rm APB}$ は $\triangle {\rm PBQ}$ の外角となるため
$\angle {\rm APB} > \angle a$・・・②
(ウ) 外部にある場合
${\rm AP}$ と円周との交点を ${\rm Q}$ とすると $\angle {\rm AQB}$ は $\triangle {\rm QBP}$ の外角となるため
$\angle {\rm APB} < \angle a$・・・②
①②③より、点 ${\rm P}$ を直線 ${\rm AB}$ に対して点 ${\rm C}$ と同じ側にとったとき $\angle {\rm APB}=\angle a$ ならば点 ${\rm P}$ は円 ${\rm O}$ の円周上にあるということが確かめられました。
円周角の定理:
(1) $\angle {\rm APB} = \frac{1}{2} \angle {\rm AOB}$
(2) $\angle {\rm APB} =\angle {\rm AQB}$
(3) ${\rm AB}$ が直径 $\iff$ $\angle {\rm APB}=90^{\circ}$
2点 ${\rm P,Q}$ が直線 ${\rm AB}$ について同じ側にあるとき $\angle {\rm APB}=\angle {\rm AQB}$ ならば4点 ${\rm A,B,P,Q}$ は1つの円周上にある。
円の接線:
(1) 円の接線は接点を通る半径に垂直である。
(2) 円の外の点からこの円にひいた2本の接線の長さは等しい。
円の様々な問題
本節では、円に関する様々な問題について考えていきましょう。色々な性質について要点内にまとめてあるので、確認しておきましょう。ここでは応用問題として、円を利用した $\sqrt{a}$ の長さの線分の描き方についてみていきましょう。
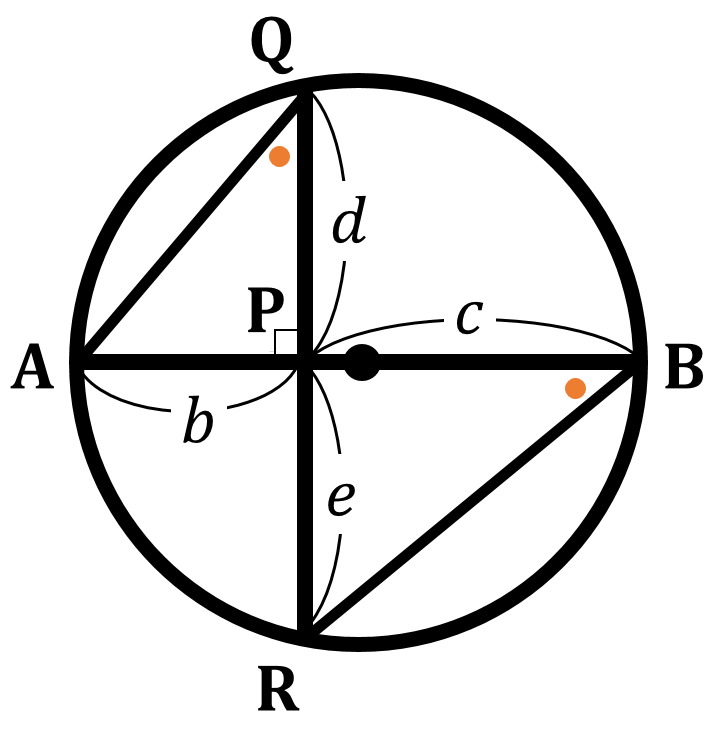
$\sqrt{a}$ の長さの線分は以下の手順で描くことができます。下の図を用いて説明します。
(1) $a$ を2つの数の積で表します。
$a=bc$
(2) $b+c$ を直径とする円を描きます。
(3) 円の直径を $b:c$ に分ける点を ${\rm P}$ とします。
(4) 点 ${\rm P}$ を通る、この直径の垂線をひき、円との交点を ${\rm P,Q}$ とします。これで作図は完了です。線分 ${\rm PQ}$ の長さが $\sqrt{a}$ となるのですが、以下にその証明を示します。
$\triangle {\rm QPA}$ と $\triangle {\rm BPR}$ において
円周角の定理より
$\angle {\rm AQP} = \angle {\rm RBP}$・・・①
対頂角は等しいから
$\angle {\rm QPA} = \angle {\rm BPR}$・・・②
①②より2組の角がそれぞれ等しいから
$\triangle {\rm QPA} ∽ \triangle {\rm BPR}$
よって対応する辺の比は等しいから
${\rm AP:QP=RP:BP}$
${\rm QP \times RP = AP \times BP}$
${\rm QP^2 }= b \times c$
${\rm QP} = \sqrt{bc}$
${\rm QP} = \sqrt{a}$
よって、線分 ${\rm PQ}$ の長さが $\sqrt{a}$ となります。
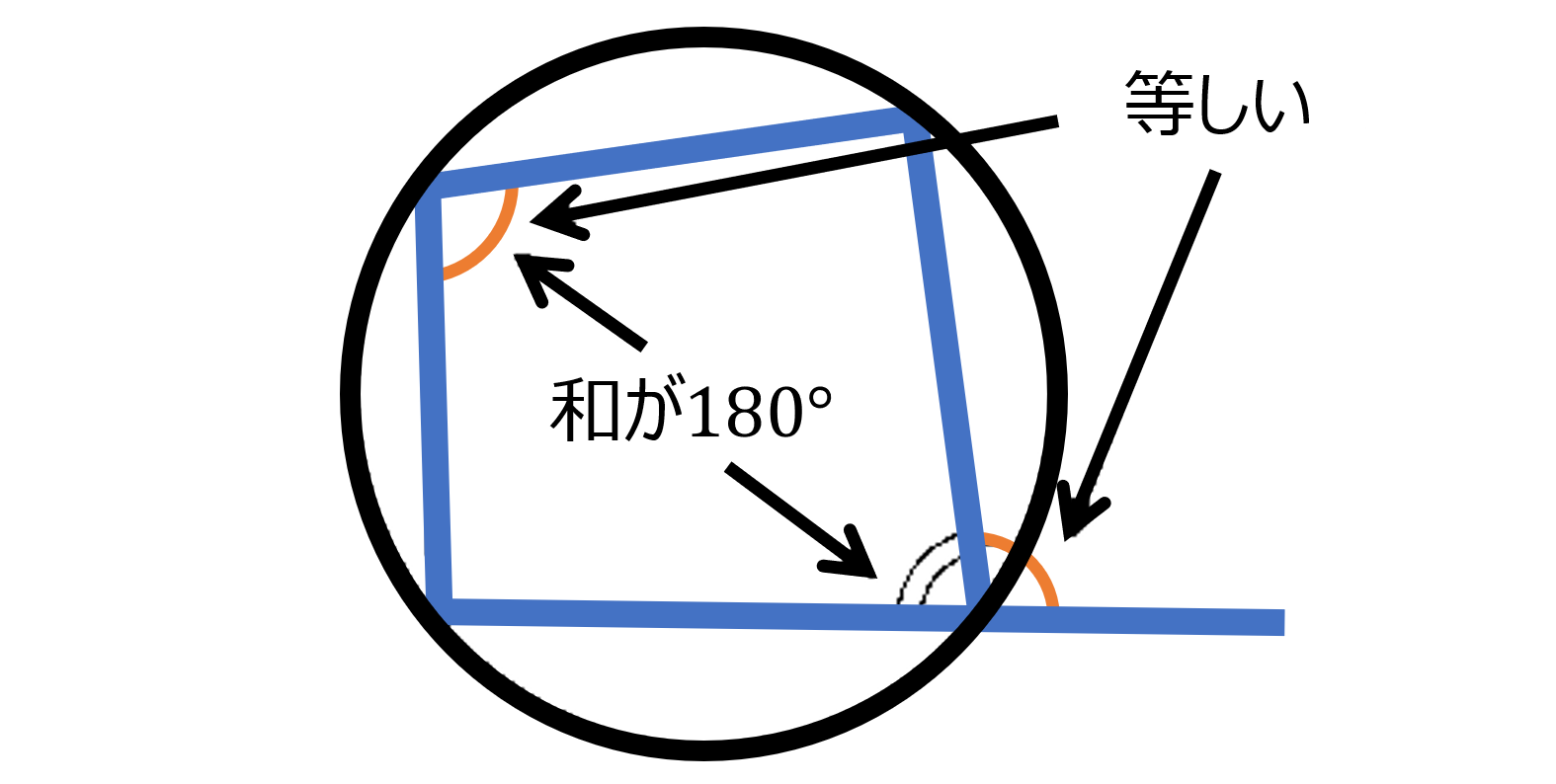
円に内接する四角形 :
(1) 四角形の対角の和は $180^{\circ}$
(2) 四角形の外角はそれと隣り合う内角の対角に等しい。