🔄 最終更新日 2021年7月15日 by takara_semi
問題
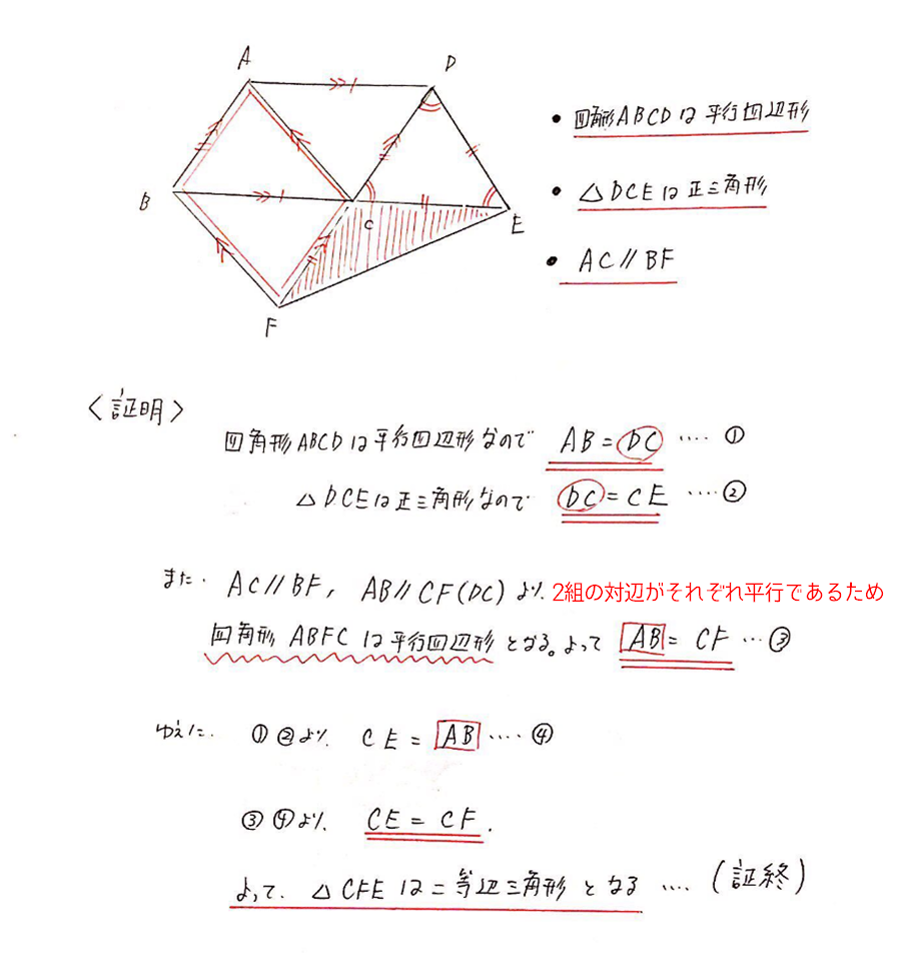
図の四角形ABCDは平行四辺形である.辺BCの延長線上に点Eをとると,△DCEは正三角形となった.また,点Bを通りACに平行な直線と辺DCの延長線との交点をFとする.このとき△CFEが二等辺去角形となることを証明せよ.

図の四角形ABCDは平行四辺形である.辺BCの延長線上に点Eをとると,△DCEは正三角形となった.また,点Bを通りACに平行な直線と辺DCの延長線との交点をFとする.このとき△CFEが二等辺去角形となることを証明せよ.

文章の条件を整理し,平行四辺形の定義を利用して正しく証明しよう
検索キーワード:
四角形ABCD, 平行四辺形, △DCEは正三角形, △CFEは二等辺三角形, 証明