🔄 最終更新日 2021年5月26日 by takara_semi
第5章:データの分析
本章では「データの分析」について学習する.
データの分析方法
❶ データの管理
データを管理・分析する上で重要となる用語を確認する.試験などで問題文を正しく理解し,解答できるように,丸暗記ではなく,それぞれの意味や必要性を正確に理解しておくことが望ましい.
(a) 変量・データ
テストの点数や,身長・体重,運動の記録などのように,ある特性を表す数量を「変量」という.そして,ある変量の測定値や観測値の集まりを「データ」という.
(b) 度数分布表・階級値・ヒストグラム
データのとる値を,いくつかの区間に区切って階級を定め,各階級に度数を対応させた表を「度数分布表」という.また,各階級の中央の値を「階級値」という.そして,度数分布表を柱状のグラフで表したものを「ヒストグラム」という.
❷ 代表値
データを代表する値のことを「代表値」という.よく用いられる代表値として「平均値」があるが,それ以外の代表値として「最頻値」や「中央値」などの指標も非常に利便性が高い.それぞれについて,以下で説明する.
(c) 平均値
変量 $x$ のデータの値が $x_1,x_2,…,x_n$ であるとする.このとき,データの平均値 $\overline{x}$ は以下のようにして計算できる.
平均値は「テストの平均点」「都道府県の平均年齢」などでもよく目にする,最も馴染み深い代表値だといえる.
(d) 最頻値 (モード)
データにおいて,最も個数の多い値を「最頻値」もしくは「モード」という.データが度数分布表に整理されているときは,度数が最も大きい階級の階級値が「最頻値」となる.
(e) 中央値 (メジアン)
データを値の大きさの順に並べたとき,その中央の位置にくる値を「中央値」もしくは「メジアン」という.データの大きさ(データの個数)が偶数のときは,中央の2つの値の平均値がそのデータの中央値となる.
❸ データの散らばりと四分位数
データを分析し,その特徴を理解する上で,値の散らばり具合を調べることは重要である.そのようなデータの特徴を非常に分かりやすく示す図として「箱ひげ図」がよく用いられる.箱ひげ図の読み解きは,データの特徴の理解を大きく助けるため,確実に理解しておくこと.
(f) 箱ひげ図
データの分布を「最小値」「第1四分位数 $Q_1$」「中央値 $Q_2$」「第3四分位数 $Q_3$」「最大値」の5つの値で表した以下のような図を「箱ひげ図」という(平均値を記入することもある).
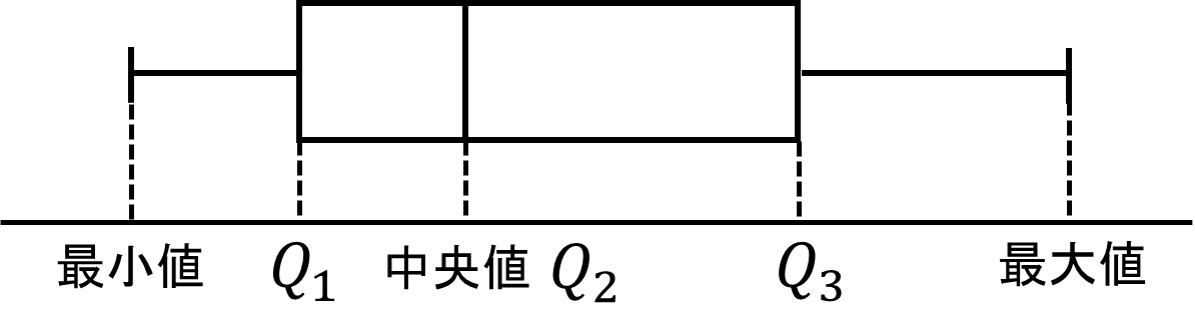
(g) 範囲
データの最大値から最小値を引いた差のことを「範囲」という.
(f) 四分位数
データの値を大きさの順に並べたとき,4等分する位置の値を「四分位数」という.四分位数は,小さい方から順にそれぞれ,第1四分位数($Q_1$),第2四分位数($Q_2$),第3四分位数($Q_3$)という.第2四分位数はデータの中央値と同値となる.
(i) 四分位範囲
データの第3四分位数 $Q_3$ と第1四分位数 $Q_1$ の差を四分位範囲という.箱ひげ図を描いた時の箱部分の幅の大きさに相当する.
(j) 四分位偏差
四分位範囲の半分の値を「四分位偏差」という.
様々な統計に関する用語の定義を理解する必要があるが,基本的考え方を理解しておけば,丸暗記することなく覚えることができる.「範囲」と「四分位数」の考えを理解していれば「四分位範囲」は自然と理解でき,また「偏差」と「四分位数」の考えを理解していれば「四分位偏差」を理解することができる.
❹ 分散と標準偏差
$x_1,x_2,…,x_n$ を変量 $x$ のデータの値とする.
(k) 偏差
データの各値と平均値 $\overline{x}$ との差を「偏差」といい以下のように定義される.
(l) 分散
偏差の2乗の平均値を「分散」といい,データの散らばり具合を示す非常に有効な指標として用いられ $s^2$ で表す.分散は以下のようにして計算する.
(ii) ($x$ のデータの分散) = ($x^2$ のデータの平均値) – ($x$ のデータの平均値$)^2$
(m) 標準偏差
分散の正の平方根を「標準偏差」といい $s$ で表す.標準偏差は以下のようにして計算する.
(ii) ${\scriptsize (x のデータの標準偏差)}$ = ${\scriptsize \sqrt{ (x^2 のデータの平均値)-(xのデータの平均値)^2}}$
❺ データの相関
(n) 散布図
2つの変量からなるデータを平面上に図示したものを「散布図」という.散布図を調べることで,得られたデータに「正の相関がある」のか「負の相関がある」のか「相関がない」のかを,知ることができる.散布図において,正の相関があるとき,データを表す点は全体的に右上がりとなり,負の相関があるとき,データを表す点は全体的に右下がりとなる.
(*) 正の相関:一方の変量が増加すると他方も増加する傾向がみられるとき,2つの変量には「正の相関がある」という.
(**) 負の相関:一方の変量が増加すると他方が減少する傾向がみられるとき,2つの変量には「負の相関がある」という.
(0) 相関係数
相関の正負と強弱を表す値として「相関係数」がある.2つの変量 $x,y$ からなるデータにおいて $(x-\overline{x})(y-\overline{y})$ の総和を $a$,$(x-\overline{x})^2$ の総和を $b$, $(y-\overline{y})^2$ の総和を $c$ とするとき,以下のようにして計算される値 $r$ を $x$ と $y$ の相関係数という.
※ 総和の記号 $\sum$ を用いれば,相関係数は
と表すことができる.
相関係数 $r$ が $1$ に近いほど「正の相関(右肩上がり)」が強く,$-1$ に近いほど「負の相関(右下がり)」が強い.また,相関がない(バラバラのデータのとき)とき,$r$ は $0$ に近い値をとる.
発展・応用
❶ 変量の変換
$a,b$ は定数とする。変量 $x$ のデータから $y=ax+b$ によって新しい変量 $y$ のデータが得られるとき,$x,y$ のデータの平均値を $\overline{x},\overline{y}$,分散を ${s_x}^2, {s_y}^2$,標準偏差を $s_x, s_y$ とすると,以下の関係が成り立つ.
${s_y}^2=a^2{s_x}^2$
$s_y=|a|s_x$
補足・詳説
❶ 表計算ソフトによるデータの分析
Excelなどの表計算ソフトでデータを分析する際に,平均値,分散,標準偏差,相関係数を計算するためには以下のようなコードを入力すればよい.
データ A1 から A5 について:
(i) 平均値を求める場合は以下のように入力する.
=AVERAGE(A1:A5)
※ 平均は英語で”AVERAGE”であるためAVERAGEと書く.
(ii) 分散を求める場合は以下のように入力する.
=VARP(A1:A5)
※ 分散は英語で”VARiance”であり,データから母集団(“Population”)の分散を算出するため(与えられたデータの一部を用いて計算した分散ではない,という意味)VARPと書く.
(iii) 標準偏差を求める場合は以下のように入力する.
=STDEVP(A1:A5)
※ 標準偏差は英語で”STandard DEViation”であり,データから母集団(“Population”)の標準偏差を算出するため(与えられたデータの一部を用いて計算した標準偏差ではない,という意味)STDEVPと書く.
(iv) データ A1 から A5,B1 からB5 の相関係数を求める場合は以下のように入力する.
=CORREL(A1:A5, B1:B5)
※ 相関係数は英語で”CORRELation coefficient”であるためCORRELと書く.

