🔄 最終更新日 2020年5月3日 by takara_semi
ポアソン分布とコンビニ
本記事では具体的な例題を扱い「統計モデル」について説明します。統計モデルはGLM、GLMM、階層ベイズモデルなど沢山ありますが、ここでは一般化線形モデル（GML）のポアソン回帰を扱います。まず、回帰を行うデータセットを生成し、準備します。今回はフリーの統計解析ソフトであるRを利用して、ポアソン分布に従う乱数生成関数を用いコンビニの来店者数の架空のヒストグラムデータを生成します。ポアソン分布に与えるパラメータとして、１日の来客数が平均800人（$\lambda=800$）のコンビニを考えます。つまり、ある日$i$において来客数が$y_i$である確率$p(y_i|\lambda_i)$は
\begin{equation}
p(y_i|\lambda_i)=\frac{\lambda_i^{y_i}\exp(-\lambda_i)}{y_i!}
\end{equation}
と表現することできます。この確率分布に従う１年間(365日分)のコンビニの来客数の架空データセットを生成し、そのデータに適する統計モデルを考えます。ここで「来客数」はカウントデータであり「負」の値は取らないことに注意して下さい。Rを用いて生成したポアソン分布に従う架空データのヒストグラムをFig1に示します。
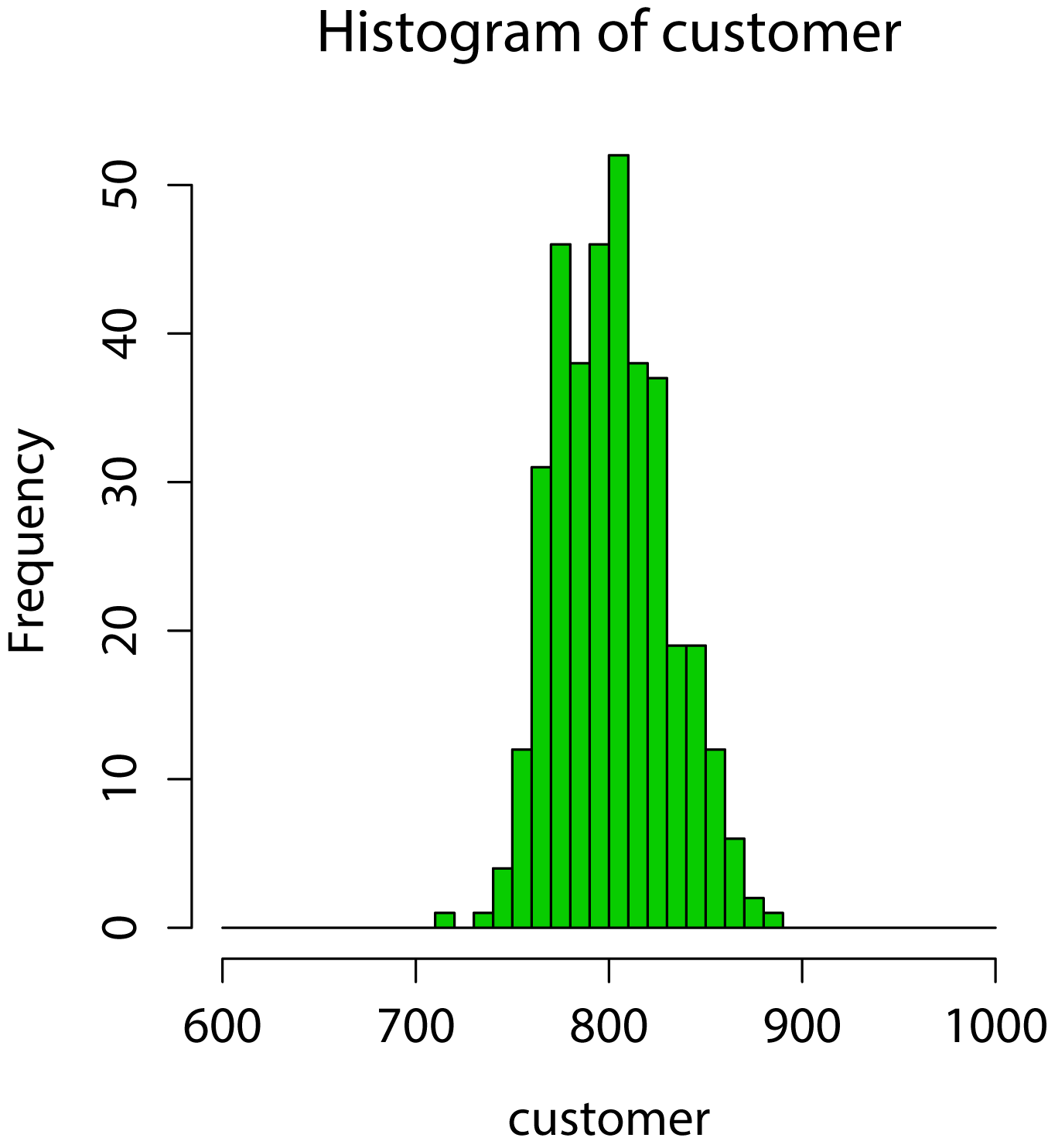
<br /> #ポアソン分布に従う架空データの生成<br /> customer <- rpois(365,lambda=800)#コンビニの来客数データ<br /> hist(customer,breaks=seq(600,1000,10),col=3)<br />
ポアソン分布によるフィッティング
Fig1で与えられたデータに対し、適当な統計モデルは何かを考えます。データに合った統計モデルを選択しなければ、うまくデータとフィットする回帰結果は得られません。今回はポアソン分布に従うデータセットであることが分かっているので、ポアソン分布を用いた回帰を行います（未知データが与えられたときは、回帰に用いる統計モデルを検討するのが大変重要な作業になります。データに隠された統計的性質を見つけるために、様々な統計モデルひとつひとつに対して、分散がどの程度かなどを検証・確認する必要などがあります）。
続いて、ポアソン分布をFig1のヒストグラムを当てはめてみます。この時、ポアソン分布のパラメータ$\lambda$を変化させて、データとのフィッティングの程度を観察してみます（このパラメータの調整作業も、未知データに対する回帰を行う際には重要となります）。パラメータ$\lambda$を変化させた場合のモデルフィッティングの結果をFig2に示します。Fig2から見て取れるように、今回の架空データに対してはパラメータ$\lambda=800$の時に良好な一致が見られます。これは最初に仮定したパラメータ（１日の来客数が平均800人：$\lambda=800$）と一致する結果です。
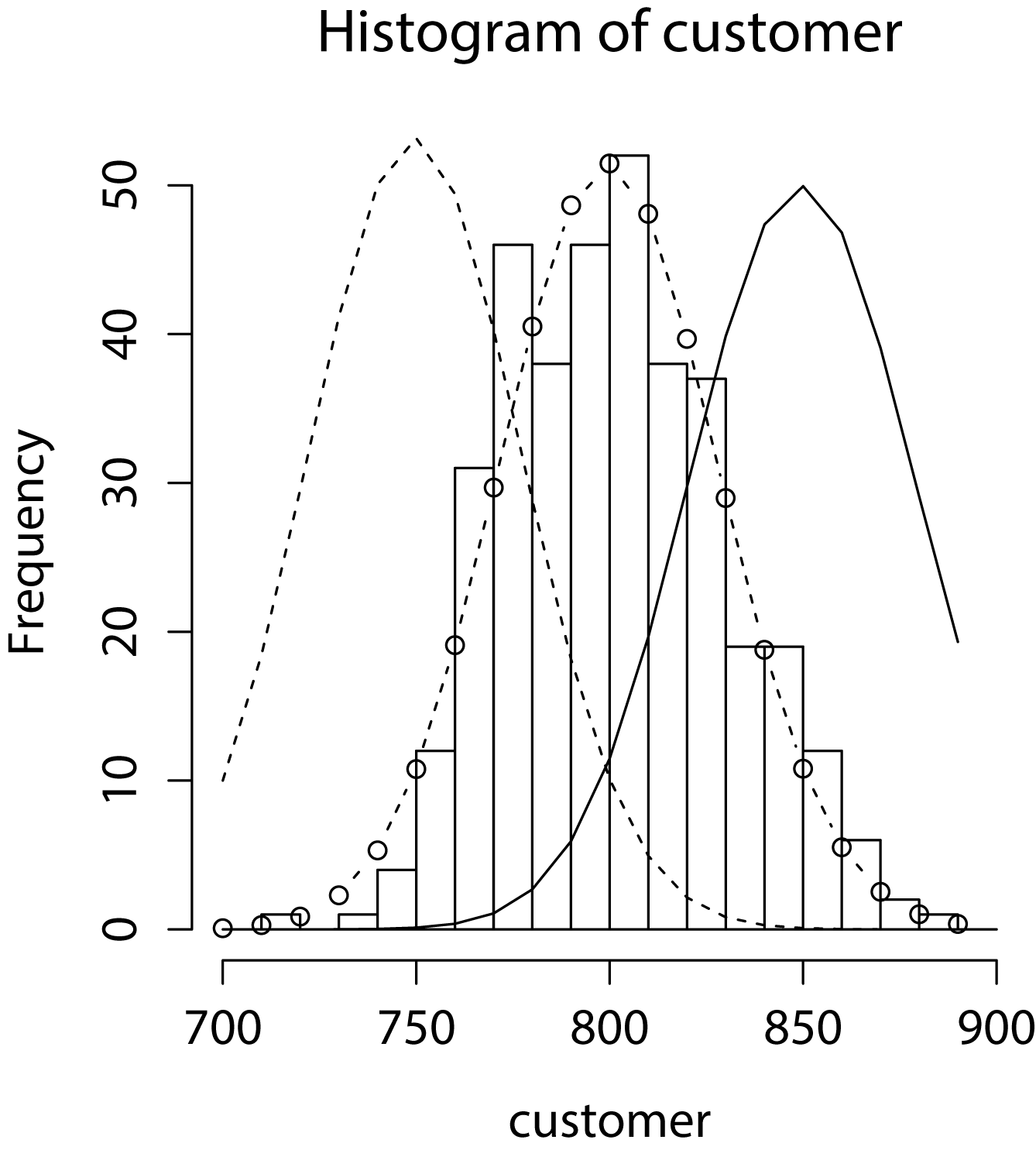
ポアソン回帰の方法
ここからは、GLMとしてポアソン回帰モデルを導入し、パラメータ$\lambda_i$を推定し、モデルフィッティングを行います。つまり、与えられたコンビニ来客数データ（Fig1）に当てはまりの良いポアソン回帰モデルのパラメータ$\lambda_i$を推定し、実際のデータに推定した回帰モデルが良好な一致を示すかどうかの検証を行います。
今回の架空データは$\lambda=800$で固定されたポアソン分布に従い生成されたデータですが、GLM導入のため、ある日$i$の来客数$\lambda_i$がコンビニの前の交通量$x_i$に依存し、その日の平均来客数が$\lambda_i$となるとして考えます。そうすると、各日$i$ごとに異なる$\lambda_i$を、交通量$x_i$の関数として次のように表現できます。
\begin{equation}
\lambda_i=f(x_i)=\exp(\beta_1+\beta_2 x_i)
\end{equation}
ここで$\beta$はポアソン回帰によって推定するパラメータです。上式は両辺の対数をとることで
\begin{equation}
\log\lambda_i=\beta_1+\beta_2 x_i
\end{equation}
と変形できます。右辺はパラメータ$\beta$の線形結合で表現されることから「線形予測子」と呼ばれ、左辺の関数を「リンク関数」と呼び、ここでは対数関数（対数リンク関数）として表現されています。GLMにはポアソン回帰以外にも様々ありますが、これらの概念を理解することで、他のGLMの理解にも繋がります。ポアソン回帰をする場合には、たいてい対数リンク関数が使用されます。ポアソン回帰の目的は、与えられたデータに対するポアソン分布を用いた統計モデルのあてはめであり、統計モデルの対数尤度関数$\log L(\beta_1,\beta_2)=\sum_i \log\frac{\lambda_i^{y_i}\exp(-\lambda_i)}{y_i!}$が最大になるパラメータ$\hat{\beta}_1$および$\hat{\beta}_2$の推定値を決定することです。生成した架空データに対し、ポアソン回帰を実行すると次のような結果が得られます。
<br />
> glm.customer<-glm(NUM~TRAFFIC,data=customer.data,family=poisson(link="log"))<br />
> summary(glm.customer)<br />
Call:<br />
glm(formula = NUM ~ TRAFFIC, family = poisson(link = "log"),<br />
data = customer.data)<br />
Deviance Residuals:<br />
Min 1Q Median 3Q Max<br />
-3.11844 -0.77988 -0.03042 0.67193 2.98305<br />
Coefficients:<br />
Estimate Std. Error z value Pr(>|z|)<br />
(Intercept) 6.762641 0.178590 37.867 <2e-16 ***<br />
TRAFFIC -0.000739 0.001754 -0.421 0.673<br />
---<br />
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1<br />
(Dispersion parameter for poisson family taken to be 1)<br />
Null deviance: 368.48 on 364 degrees of freedom<br />
Residual deviance: 368.30 on 363 degrees of freedom<br />
AIC: 3483.9<br />
Number of Fisher Scoring iterations: 3<br />
推定した結果であるパラメータ$\hat{\beta}_1$および$\hat{\beta}_2$を代入すると
\begin{equation}
\lambda_i=\exp(\hat{\beta}_1+\hat{\beta}_2 x_i)
\end{equation}
が得られ、上式によりデータフィッティング（回帰）を実行した結果をFig3に示します。Fig3を見るとポアソン回帰によって推定された回帰モデルが確かに当てはまりが良いことが確認できました。以上で、ポアソン回帰の完了です。
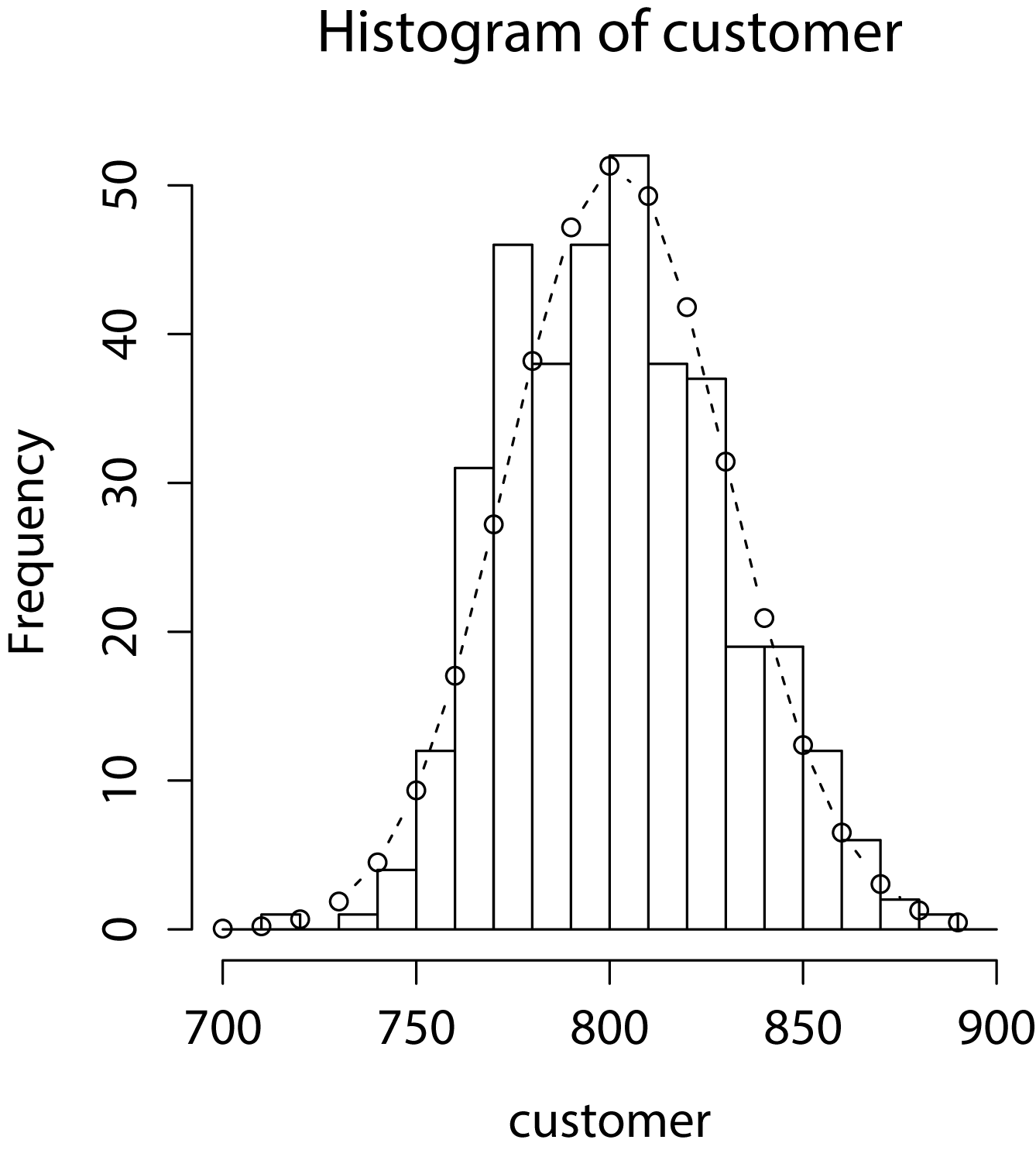
<br /> #ポアソン分布に当てはめる<br /> y<-seq(length=20, from=700, by=10)<br /> prob.1<-dpois(y,lambda=800)<br /> prob.2<-dpois(y,lambda=750)<br /> prob.3<-dpois(y,lambda=850)<br /> hist(customer,breaks=seq(700,900,10),col=0)<br /> lines(y,prob.1*3650,type="b",lty=2)<br /> lines(y,prob.2*3650,type="l",lty=2)<br /> lines(y,prob.3*3650,type="l",lty=1)</p> <p>#ポアソン回帰を行う<br /> day<-seq(length=365,from=1,by=1)<br /> traffic<-seq(length=365,from=100,by=0.01)<br /> customer.data<-data.frame(DAY=day,NUM=customer,TRAFFIC=traffic)<br /> glm.customer<-glm(NUM~TRAFFIC,data=customer.data,family=poisson(link="log"))<br /> summary(glm.customer)</p> <p>#ポアソン回帰の推定結果でフィッティング<br /> lambda.pre<-glm.customer$coefficients["(Intercept)"]+glm.customer$coefficients["TRAFFIC"]*traffic<br /> prob.pre<-dpois(y,lambda=exp(mean(lambda.pre)))<br /> hist(customer,breaks=seq(700,900,10),col=0)<br /> lines(y,prob.pre*3650,type="b",lty=2)<br />
統計モデルは、見かけの変動を示すデータの中に埋もれた真の姿を把握するための重要なツールです。実際に手を動かしてモデル回帰を実行することで、古典的な線形モデルにおける誤差項に仮定されていた正規分布の枠組みを外し、正規分布になじまない確率変数に対しても、統一的な線形推測が可能であることが理解できたことでしょう。また、コンビニの来客数以外に、例えば累積被ばく線量と死亡相対リスクに関する統計データの解析には、過去の研究で実際にポアソン回帰モデルが適用されています。様々なデータに隠された統計的性質を、統計モデルを上手く設計することで見つけることができれば、未解決状態にある社会問題の解決の大きな助けになることは間違いないでしょう。
＜参考文献＞
[1] 丹後俊郎．”統計モデル入門”．朝倉書店(2000)
[2] 金 明哲．”Rによるデータサイエンス”．森北出版(2007)
