🔄 最終更新日 2020年4月12日 by takara_semi
パラメトリック回帰とノンパラメトリック回帰
身近にあるデータを解析する際、プロットしたときに明示的な統計的性質が分からない場合が多くあります。そうすると、解析のために、利用する統計モデルを検討する必要があります。例えばパラメトリック回帰ではある程度の目途をつけてモデルを仮定し、与えられたデータと最も上手くフィットするモデルパラメータを最尤法などを用いて推定することで、データを上手く表現するモデル(数式)を得ることができます。しかし実際には、先述の通り、事前の予想ではモデルを上手く仮定できない場合が多くあります。そこで、仮定するモデルの形自体を与えられたデータから推定する回帰手法があり、そのような手法はノンパラメトリック回帰と呼ばれます。
ハエの寿命の回帰
本記事では、Rのパッケージに含まれるサンプル・データセットの中から「ハエの寿命に関するデータ(medflies.csv)」を用いて、ノンパラメトリック回帰の方法を適用して解析します。解析するデータセットの散布図をFig1およびFig2に示します。
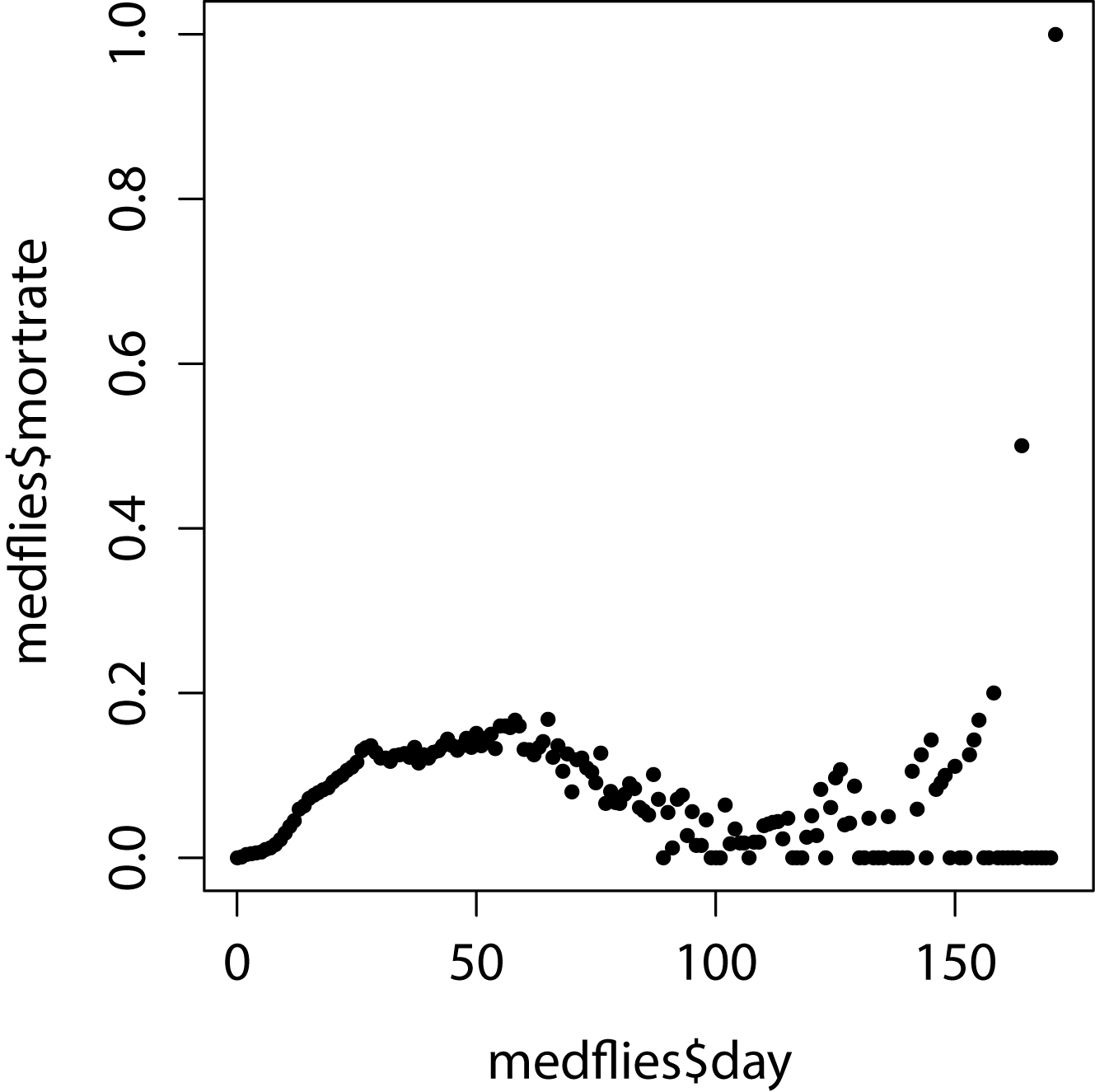
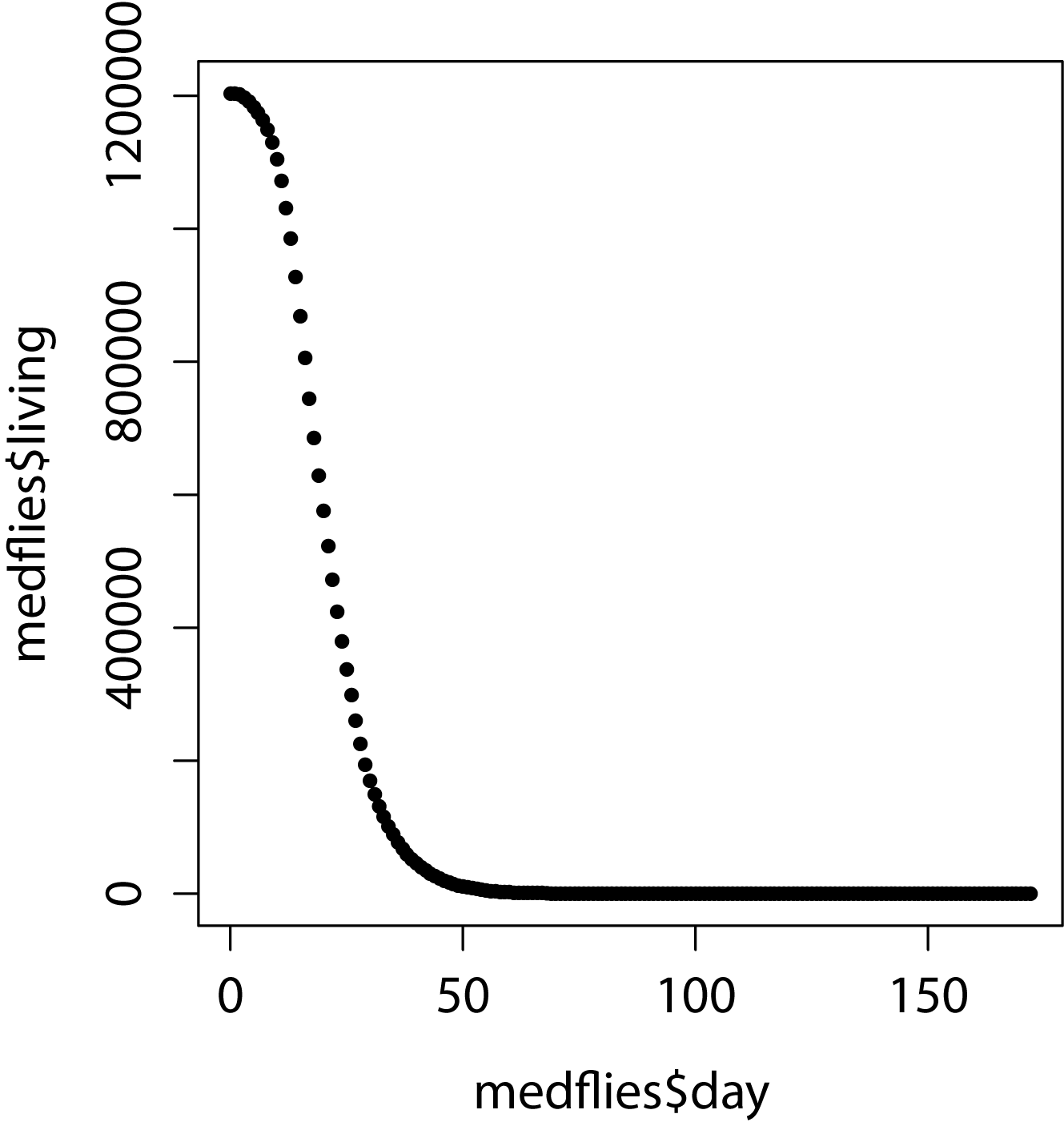
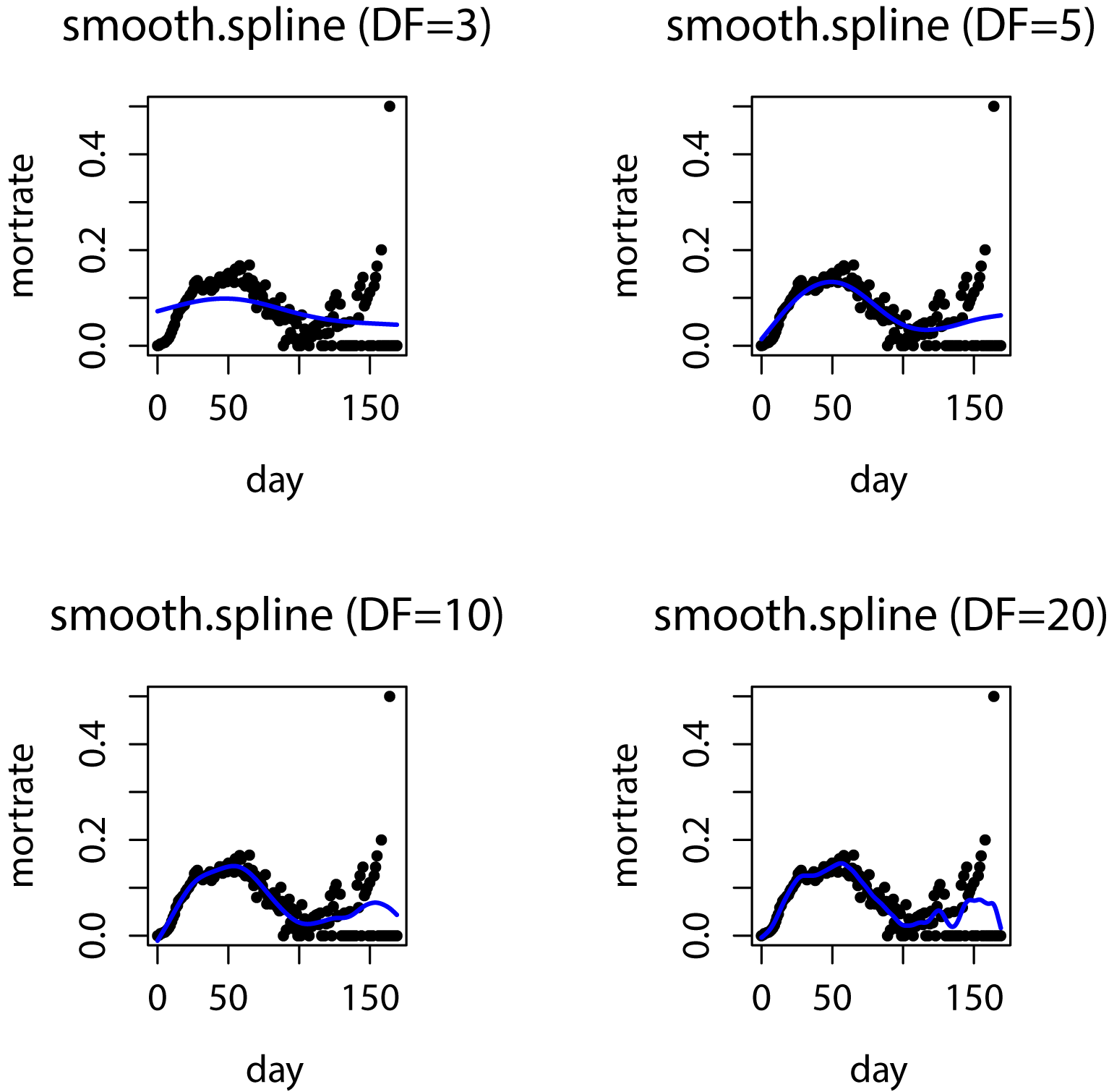
Fig1のデータセットに対する回帰結果をFig3に示します。Fig3はパラメータDF(等価自由度)によって、回帰結果がどのように変化するかを検証した結果です。この結果からDFが大きいほど回帰する関数がひとつひとつのデータ点を忠実になぞるような形に変化する様子が見て取れます。つまり、DFを変化させることで、モデル自体の複雑さを調整することができることが分かります。今回のデータセットに対してはDF=5の場合がおおよそ良好な回帰を実現しています。
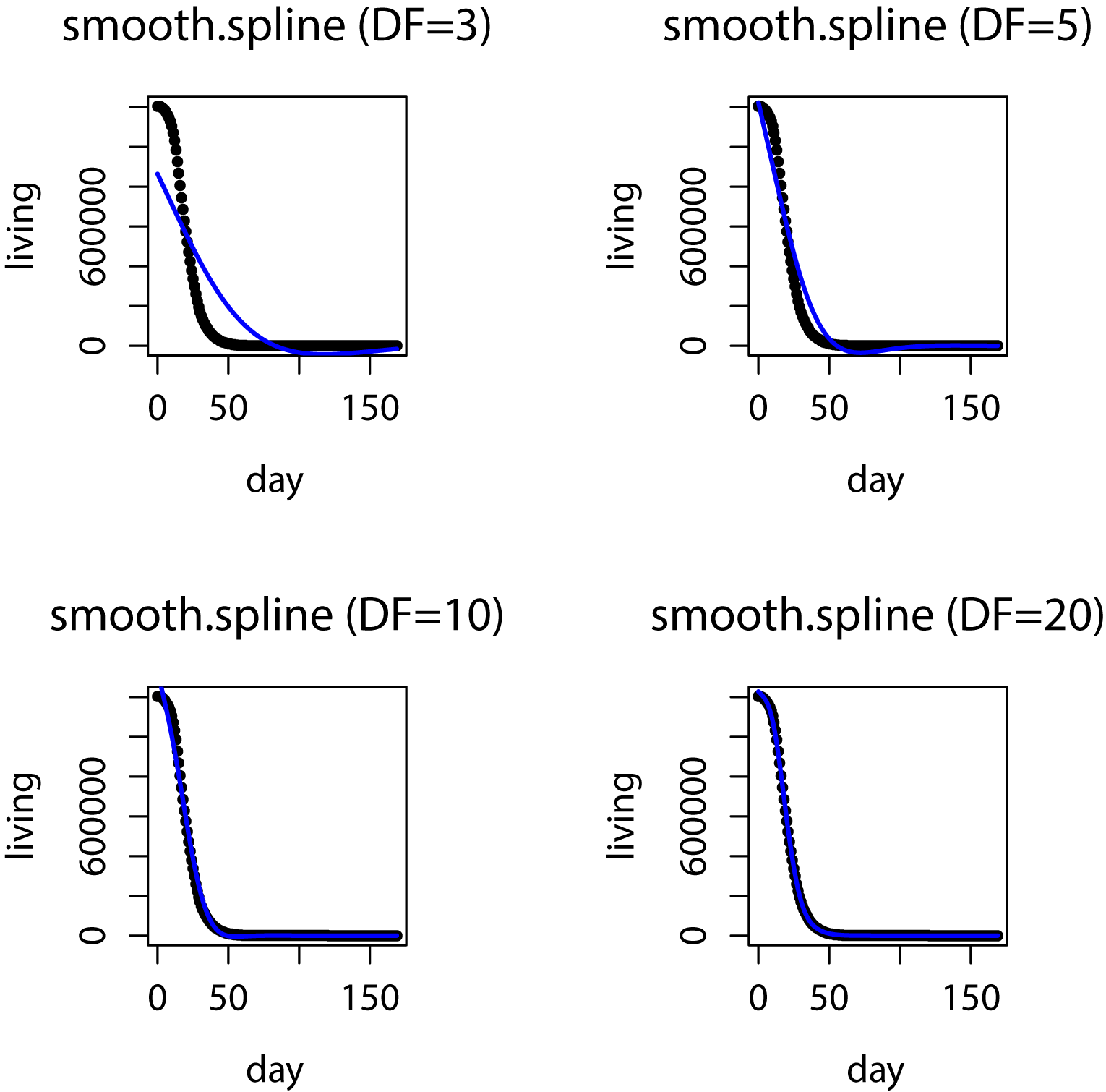
またFig2のデータセットに対する回帰結果をFig4に示します。Fig4はFig3と同様、パラメータDF(等価自由度)によって、回帰結果がどのように変化するかを検証した結果です。この結果からもDFが大きいほど回帰する関数がひとつひとつのデータ点を忠実になぞるような形に変化する様子が見て取れます。今回のデータセットに対してはDF=20の場合において実データとの誤差がほとんど見られない程、精度の良い回帰結果が得られました。これはFig1のデータに比べFig2のデータは外れ値が少なく整ったデータセットで、回帰が容易であったためだと考えられます。
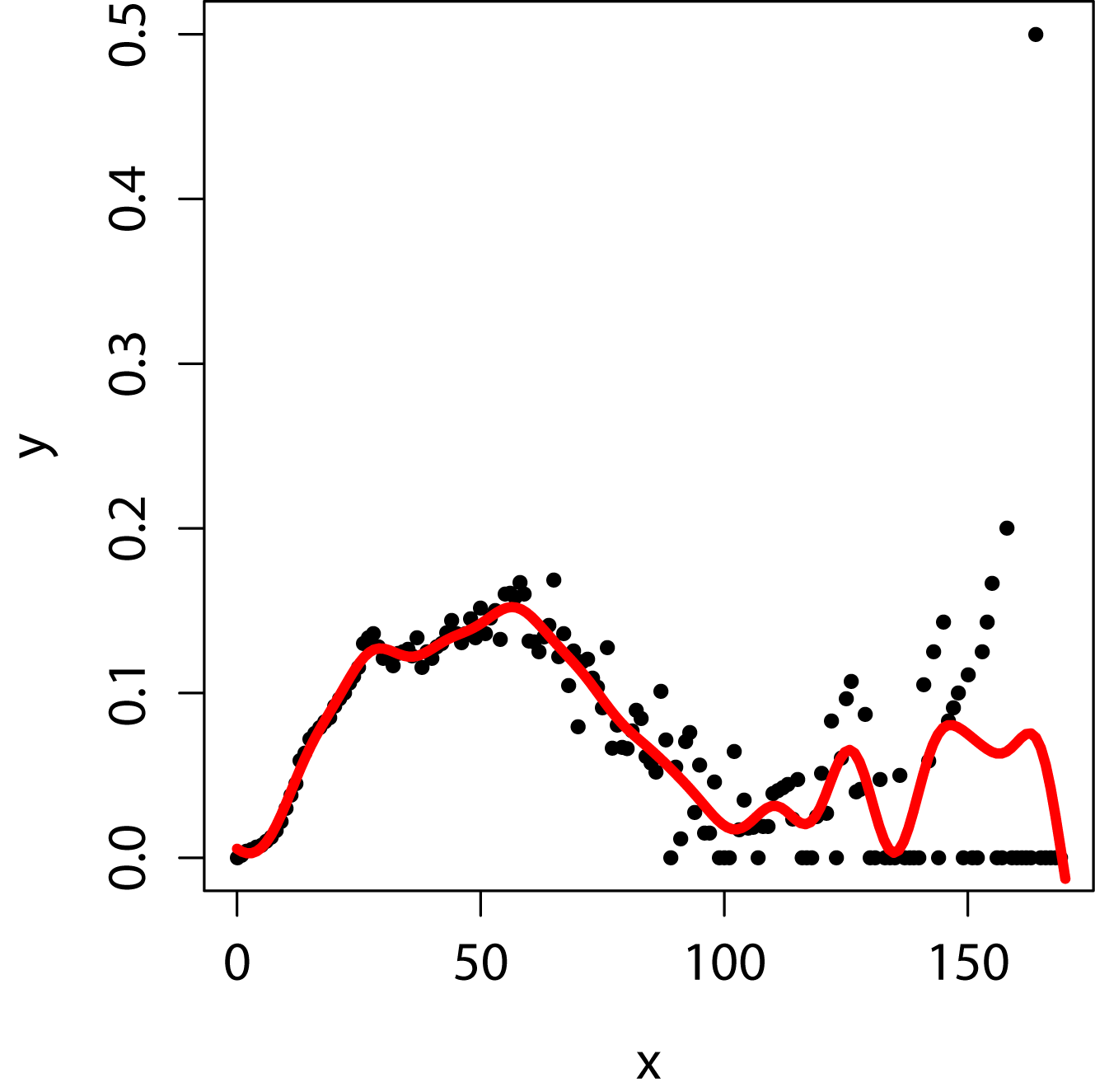
回帰の他の例としてFig1のデータに対してガウスカーネルを用いた回帰を実行した結果をFig5に示します。このモデルにおいてもsmooth.splineを用いたノンパラメトリック回帰におけるDFと同様の働きをするハイパーパラメータ$\sigma$を調整することで、データに沿った良好な回帰を実現することができます(Fig5はある程度良好な回帰結果が得られた時の回帰例を示したものです)。
ノンパラメトリック回帰の利点と欠点
ノンパラメトリック回帰の手法の利点は、パラメトリック回帰と比較して、ハイパーパラメータの調整によってオーバーフィッティングを避ける事ができることや、モデルの複雑さ自体を推定することができること(複雑さを明に扱う必要がない)などが挙げられます。モデルの複雑度は、モデルの表現力を測るための尺度になります。ガウシアンカーネルを用いた場合は、パラメータ$\sigma$の値によって、回帰モデルの複雑さを調整することができます。これらの特徴はノンパラメトリック回帰特有のものであり、パラメトリック回帰と比較し優位な点です。ノンパラメトリック回帰の欠点としては、扱うデータ数の増加に伴う計算コストや要するメモリの増加などが挙げられます。結局のところ、それぞれの回帰手法の特徴を理解した上で、与えられたデータによって、適当な手法を判断する必要があるといえます。
以下のコードをR Studioなどで実行すれば、本記事中の結果をすべて再現することができます。
<br /> library(SemiPar)<br /> medflies<-read.table("medflies.csv",header=T, sep=",")#チチュウカイミバエの死亡率のデータ<br /> plot(medflies$day,medflies$living,pch=20)#その日の初めに生きているチチュウカイミバエの数<br /> plot(medflies$day,medflies$mortrate,pch=20)#その日までのハエの死亡率<br /> dim(medflies)</p> <p>#スプライン回帰(smooth.spline)<br /> ##その日までのハエの死亡率のノンパラメトリック回帰<br /> par(mfrow=c(2,2))<br /> medflies.ss <- smooth.spline(medflies[1:170,1], medflies[1:170,3], df=3);medflies.ss<br /> plot(medflies[1:170,-2], pch=20, main="smooth.spline (DF=3)")<br /> lines(spline(medflies.ss$x,medflies.ss$y), col = "blue", lwd=2)<br /> medflies.ss <- smooth.spline(medflies[1:170,1], medflies[1:170,3], df=5);medflies.ss<br /> plot(medflies[1:170,-2], pch=20, main="smooth.spline (DF=5)")<br /> lines(spline(medflies.ss$x,medflies.ss$y), col = "blue", lwd=2)<br /> medflies.ss <- smooth.spline(medflies[1:170,1], medflies[1:170,3], df=10);medflies.ss<br /> plot(medflies[1:170,-2], pch=20, main="smooth.spline (DF=10)")<br /> lines(spline(medflies.ss$x,medflies.ss$y), col = "blue", lwd=2)<br /> medflies.ss <- smooth.spline(medflies[1:170,1], medflies[1:170,3], df=20);medflies.ss<br /> plot(medflies[1:170,-2], pch=20, main="smooth.spline (DF=20)")<br /> lines(spline(medflies.ss$x,medflies.ss$y), col = "blue", lwd=2)<br /> par(mfrow=c(1,1))</p> <p>#その日の初めに生きているチチュウカイミバエの数のノンパラメトリック回帰<br /> par(mfrow=c(2,2))<br /> medflies.ss <- smooth.spline(medflies[1:170,1], medflies[1:170,2], df=3);medflies.ss<br /> plot(medflies[1:170,-3], pch=20, main="smooth.spline (DF=3)")<br /> lines(spline(medflies.ss$x,medflies.ss$y), col = "blue", lwd=2)<br /> medflies.ss <- smooth.spline(medflies[1:170,1], medflies[1:170,2], df=5);medflies.ss<br /> plot(medflies[1:170,-3], pch=20, main="smooth.spline (DF=5)")<br /> lines(spline(medflies.ss$x,medflies.ss$y), col = "blue", lwd=2)<br /> medflies.ss <- smooth.spline(medflies[1:170,1], medflies[1:170,2], df=10);medflies.ss<br /> plot(medflies[1:170,-3], pch=20, main="smooth.spline (DF=10)")<br /> lines(spline(medflies.ss$x,medflies.ss$y), col = "blue", lwd=2)<br /> medflies.ss <- smooth.spline(medflies[1:170,1], medflies[1:170,2], df=20);medflies.ss<br /> plot(medflies[1:170,-3], pch=20, main="smooth.spline (DF=20)")<br /> lines(spline(medflies.ss$x,medflies.ss$y), col = "blue", lwd=2)<br /> par(mfrow=c(1,1))</p> <p>#正則化付きカーネル回帰(ノンパラメトリック回帰)<br /> #その日までのハエの死亡率のノンパラメトリック回帰<br /> library(kernlab);library(MASS)<br /> sigma <- 0.01; lambda <- 0.1; #モデルパラメータ設定<br /> n <- 170<br /> medflies<-as.matrix(medflies)<br /> x <- medflies[1:170,1]<br /> y <- medflies[1:170,3]<br /> K <- kernelMatrix(rbfdot(sigma=sigma),x)#ガウシアン・カーネル(rbfdot)のグラム行列<br /> rowK <- rowSums(K)#推定量の計算(一般逆行列を使って線形方程式を解く)<br /> A <- rbind(cbind(K%*%K+lambda*K,rowK),c(rowK,n))<br /> b <- c(K%*%y, sum(y))<br /> estpar <- as.vector(ginv(A)%*%b)<br /> beta <- estpar[1:n]<br /> b <- estpar[n+1]<br /> px <- seq(0,170,l=170)<br /> pK <- kernelMatrix(rbfdot(sigma=sigma),px,x)<br /> py <- pK%*%beta+b #予測値<br /> plot(x,y,pch=20)<br /> lines(px,py,lwd=4,col=2)<br />



