🔄 最終更新日 2023年2月4日 by takara_semi
問題
全ての実数 $x$ に対して $(m-1)x^2+(m-1)x+1>0$ が成り立つような実数 $m$ の値を求めよ.
全ての実数 $x$ に対して $(m-1)x^2+(m-1)x+1>0$ が成り立つような実数 $m$ の値を求めよ.

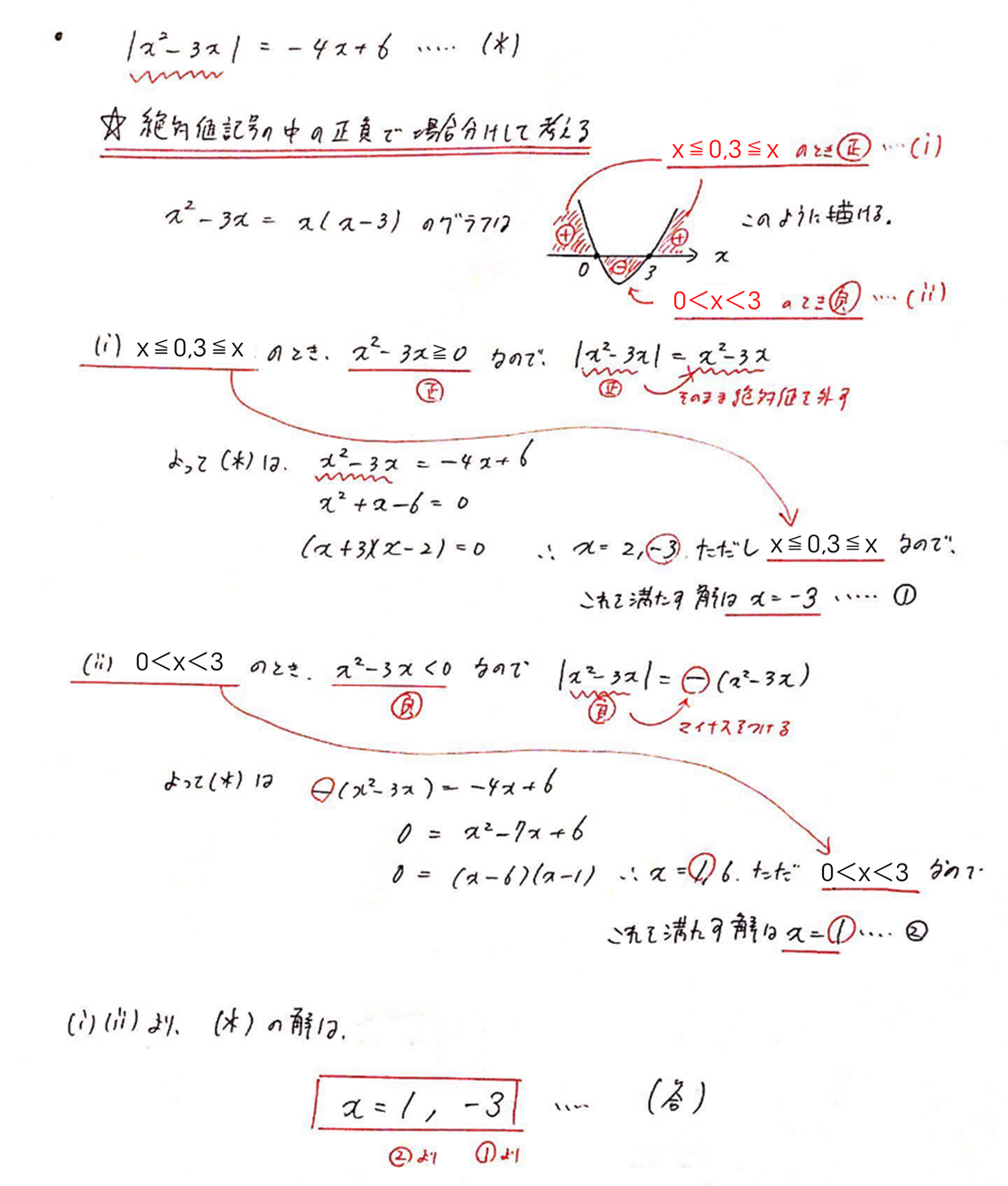
絶対値記号の中の値の正負で場合分けをして考えよう.
$|a| = \begin{cases}
a & (a≧0) \\
-a & (a<0)
\end{cases}$
検索キーワード:
全ての実数 $x$, $(m-1)x^2+(m-1)x+1>0$, 実数 $m$.