🔄 最終更新日 2022年7月26日 by takara_semi
問題
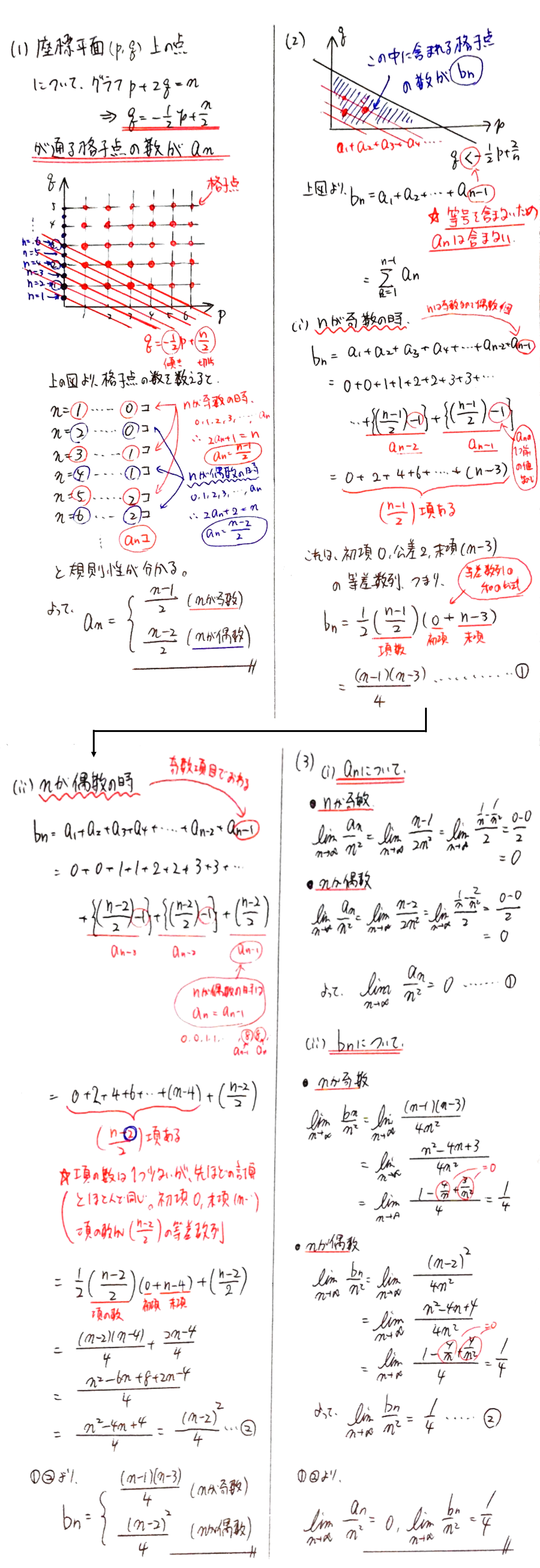
座標平面上の点 $(p,q)$ で,$p$ と $q$ がともに整数となる点を格子点という.以下の(1)~(3)を解け.
(1) 自然数 $n$ に対し,$p+2q=n$, $p>0$, $q>0$ を満たす格子点 $(p,q)$ の個数を $a_n$ とするとき,$a_n$ を求めよ.
(2) 自然数 $n$ に対し,$p+2q<n$, $p>0$, $q>0$ を満たす格子点 $(p,q)$ の個数を $b_n$ とするとき,$b_n$ を求めよ.
(3) 極限値 $$\lim_{n \to \infty} \frac{a_n}{n^2}, \lim_{n \to \infty} \frac{b_n}{n^2}$$ をそれぞれ求めよ.
座標平面上の点 $(p,q)$ で,$p$ と $q$ がともに整数となる点を格子点という.以下の(1)~(3)を解け.
(1) 自然数 $n$ に対し,$p+2q=n$, $p>0$, $q>0$ を満たす格子点 $(p,q)$ の個数を $a_n$ とするとき,$a_n$ を求めよ.
(2) 自然数 $n$ に対し,$p+2q<n$, $p>0$, $q>0$ を満たす格子点 $(p,q)$ の個数を $b_n$ とするとき,$b_n$ を求めよ.
(3) 極限値 $$\lim_{n \to \infty} \frac{a_n}{n^2}, \lim_{n \to \infty} \frac{b_n}{n^2}$$ をそれぞれ求めよ.

格子点を扱う問題は散見されますので,その扱いに慣れておきましょう.
検索キーワード:
座標平面上, 点 $(p,q)$ ,$p$, $q$, 整数, 格子点, 自然数 $n$, $p+2q=n$, $p>0$, $q>0$, $a_n$, $p+2q<n$, $b_n$, 極限値, $\lim_{n \to \infty} \frac{a_n}{n^2}$, $\lim_{n \to \infty} \frac{b_n}{n^2}$.