🔄 最終更新日 2022年4月2日 by takara_semi
問題
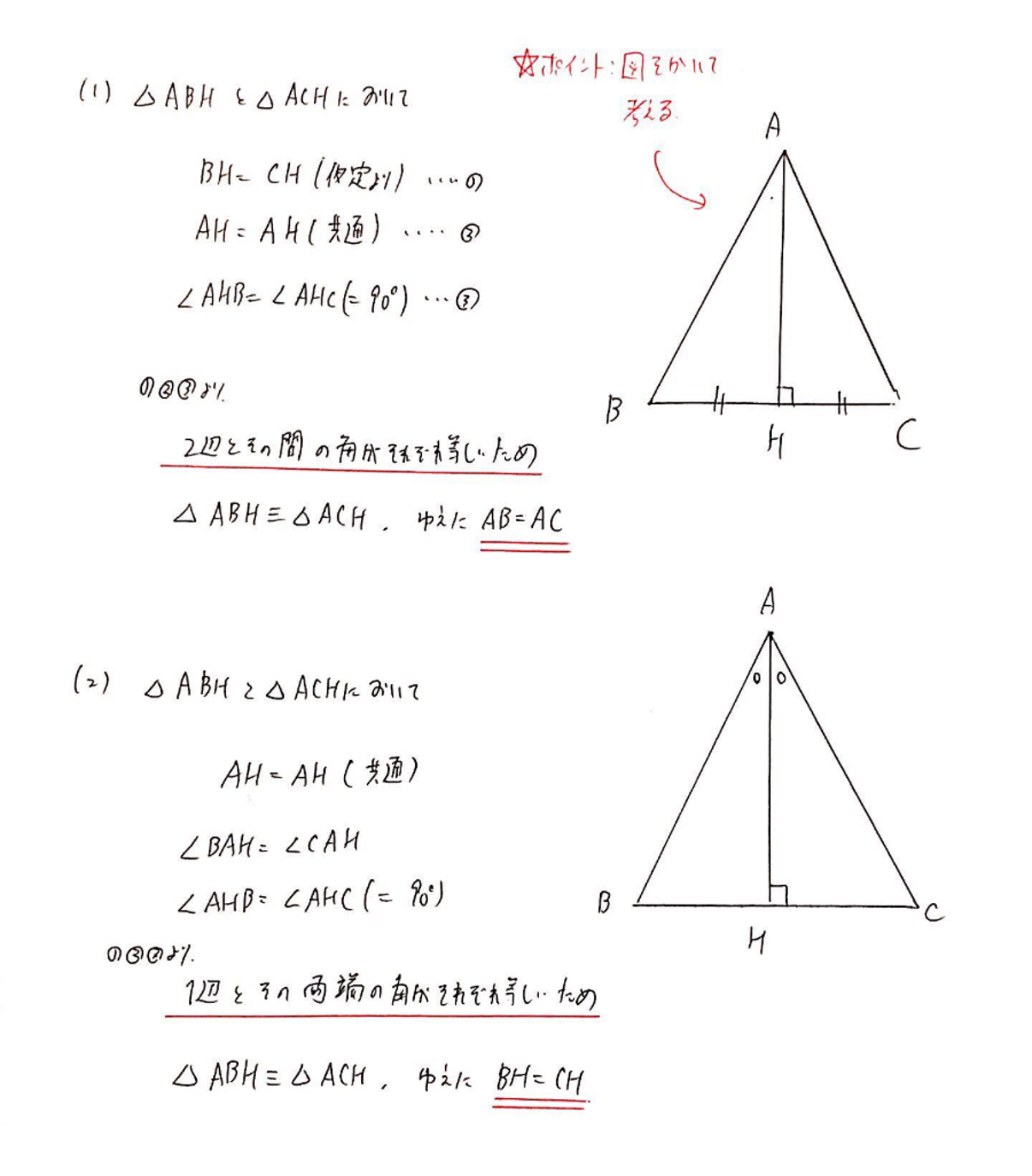
三角形 ABC において,頂点 A から辺 BC に下ろした垂線の足を H とするとき,以下が成り立つことを証明せよ.
(1) $\rm{BH}=\rm{CH}$ $⇒$ $\rm{AB}=\rm{AC}$
(2) ∠BAH=∠CAH $⇒$ $\rm{BH}=\rm{CH}$
三角形 ABC において,頂点 A から辺 BC に下ろした垂線の足を H とするとき,以下が成り立つことを証明せよ.
(1) $\rm{BH}=\rm{CH}$ $⇒$ $\rm{AB}=\rm{AC}$
(2) ∠BAH=∠CAH $⇒$ $\rm{BH}=\rm{CH}$

図形問題では,与えられた条件を満たす図をできるだけ正確に描いて考えることでケアレスミスを大きく減らすことができます.
検索キーワード:
三角形 ABC, 頂点 A, 辺 BC, 垂線の足 H, 証明, $\rm{BH}=\rm{CH}$, $\rm{AB}=\rm{AC}$, ∠BAH=∠CAH, $\rm{BH}=\rm{CH}$.