６章：確率 | タカラゼミ

各種SNSで記事を共有

🔄 最終更新日 2019年12月11日 by takara_semi

中2 ＞ 6章：確率

本章では、サイコロやルーレットの目の出方やカードゲームの手札など、偶然に左右されることがらの起こりやすさについて、実験や計算によって求める方法について考えていきましょう。身近でよくみかける確率としては、天気予報があります。天気予報は、たとえば降水確率 $30%$ は「過去に同じ気象条件が $100$ 回あったとしたときに、$30$ 回雨が降った」ということを表しているのです。なので、あくまで雨が降るかどうかを示したもので、雨の強さまでは、降水確率からは分かりません。さて、今日の降水確率が $30%$ のとき、あなたは傘を持ってでかけますか？確率を勉強すると、そのヒントや答えが見つかるかもしれません。

場合の数

本節では、確率の基礎の理解の準備として、場合の数の考え方を正しく理解しましょう。

要点

場合の数の数え方：
(1) 起こりうる場合の全部をもれなく重複なく数えあげる。それには全ての場合を順序よく整理して並べる。
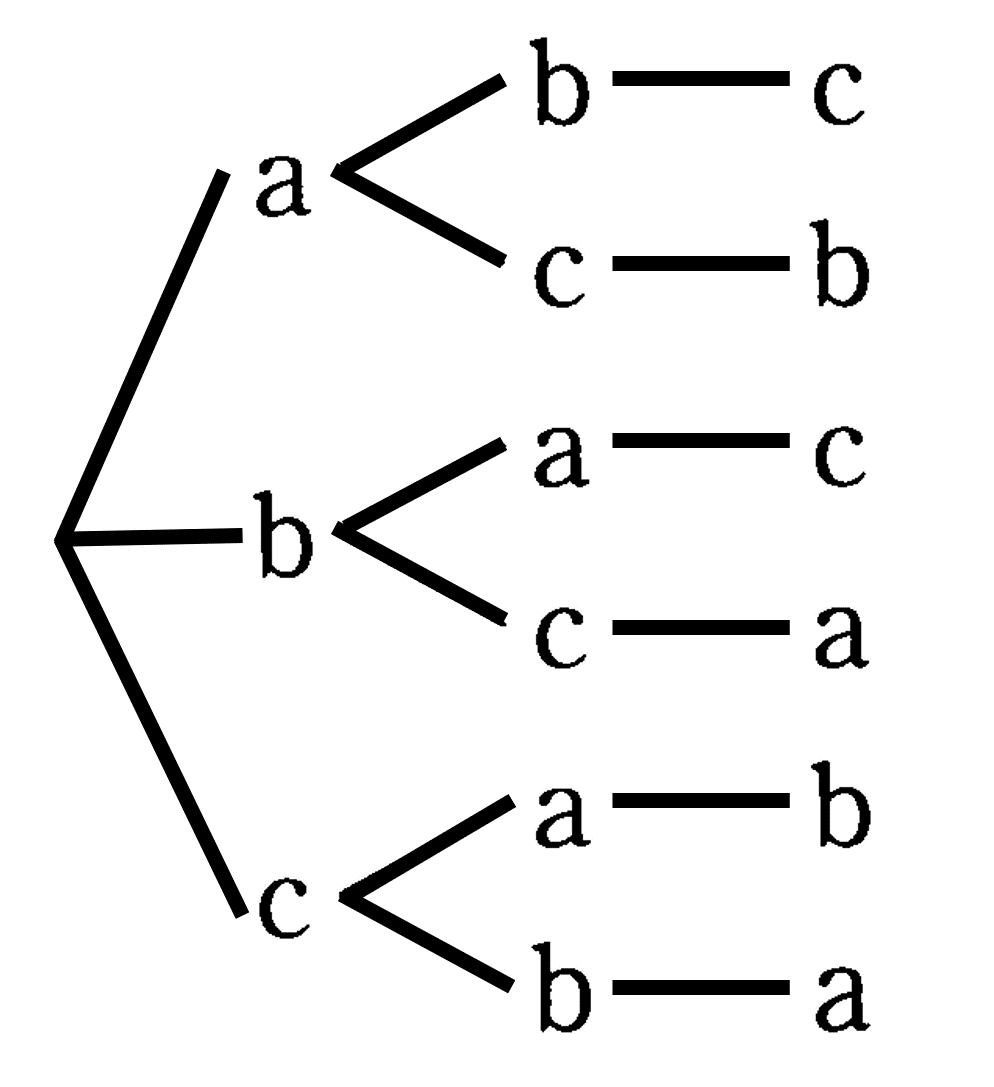
(2) 樹形図や表を用いる。$a,b,c$ を1列に並べる $\to$ 起こりうる場合を樹状に整理して列挙した図を樹形図という。
　

樹形図

数学が面白くなる動画―13　

確率を知らないとゲームに負ける？確率はゲームに勝つための強力な武器になるのです。

確率

本節では、ことがらの起こりやすさを数で表現する方法や、それを利用して物事を判断することについて考えてみましょう。例えば「コインを投げて表が出る」ということがらのように、その結果が偶然に左右される実験や観察を行う時に、そのことがらが起こると期待される程度を数で表現したものを、そのことがらの起こる確率といいます。確率が $p$ であるということは「同じ実験や観察を何度も繰り返すと、そのことがらの起こる相対度数（コインが表になる相対度数=$\frac{表向きになった回数}{コインを投げた回数}$）が $p$ に限りなく近づくという意味をもっています。例えばコインを投げる場合では、表が出ることと裏が出ることは同じ程度に期待できます。このようなとき、どの結果が起こることも同様に確からしいといいます。反対に、いかさまのコインで、どちらかの面が出やすいような仕掛けがされている場合は、同様に確からしいとはいえません。数学では特別な条件が与えられない限り、サイコロやコインなどは正しく作られているものとして扱います。

ここから、具体的な確率の計算方法について考えてみましょう。ある実験または観察を行うときに、起こりうる場合が全部で $n$ 通りあり、どの場合が起こることも同様に確からしいとします。そのうち、あることがら ${\rm A}$ の起こる場合が $a$ 通りあるとき、ことがら ${\rm A}$ の起こる確率 $p$ は $p=\frac{a}{n}$ で求めることができます。つまり、確率 $p=\frac{ことがらAの起こる場合の数}{起こり得る全ての場合の数}$ ということです。また、確率 $p$ のとりうる値は $0≦p≦1$ の範囲にあります。「必ず起こる」確率は $1$ 「決して起こらない」確率は $0$ となります。そして一般に、ことがら $A$ の起こらない確率は $(Aの起こらない確率)=1-(Aの起こる確率)$ で求めることができます。これらの知識を活用して、いろいろなことがらの確率を正しく効率的に計算できるように練習しましょう。

要点

確率：あることがらが起こることが期待されている程度の数。
同様に確からしい：全ての場合の起こり方が同じ程度に期待されていること。
(1) 確率 $=\frac{ことがらAの起こる場合の数}{起こり得る全ての場合の数}$

例　

大小2つのサイコロを投げるとき、和が $4$ になる確率を求める。起こりうる場合は全部で $6 \times 6 =36$ 通りあり、どの場合が起こることも同様に確からしい。このうち、出た目の数の和が $4$ となるのは $(1,3),(2,2),(3,1)$ の $3$ 通りあるため、求める確率は $\frac{3}{36}=\frac{1}{12}$ となる。

(2) (${\rm A}$の起こらない確率)=$1-$(${\rm A}$の起こる確率)

例　

3枚のコインを投げるとき少なくとも1枚は表が出る確率を求める。「少なくとも1枚は表が出る」というのは「3枚とも裏にはならない」と同じであることから、求める確率は全体から3枚とも裏になる確率を引けば求まる。よって $1-(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2})$$=1-\frac{1}{8}$$=\frac{7}{8}$ となる。