🔄 最終更新日 2019年12月11日 by takara_semi
中2 > 3章:1次関数
中学1年では関数の関係にある2つの数量をみつけて「比例」「反比例」の関係として問題を解決する方法を学びました。本章では、ある2つの数量の「変化の規則性」に注目することで、その関係の特徴を利用した問題解決の方法について学び、1年次より発展的な知識を習得していきましょう。
1次関数とグラフ
本節では、$y=ax+b$ という式で表される $x$ と $y$ との関係について考えます。2つの変数 $x$, $y$ について、$y$ が $x$ の1次式で表されるとき $y$ は $x$ の1次関数であるといいます。つまり、1次関数は一般に $y=ax+b$ と表されます。1年で学んだ比例の式は $y=ax$ でしたが、これは1次関数の式 $y=ax+b$ の定数 $b$ が $0$ のときの場合です。「比例」は「1次関数の特別な場合」を表していたということです。また $x$ の増加量に対する $y$ の増加量の割合を変化の割合といい、1次関数 $y=ax+b$ では変化の割合は一定で $a$ に等しくなります(※ 変化の割合 $=\frac{yの増加量}{xの増加量}=a$:比例定数 $a$ と変化の割合 $a$ の意味の違いに気を付けること。反比例の関係では変化の割合は一定ではありません。)。つまり、この一定の値 $a$ は、 $x$ の値が $1$ だけ増加した時の $y$ の増加量を表しています。
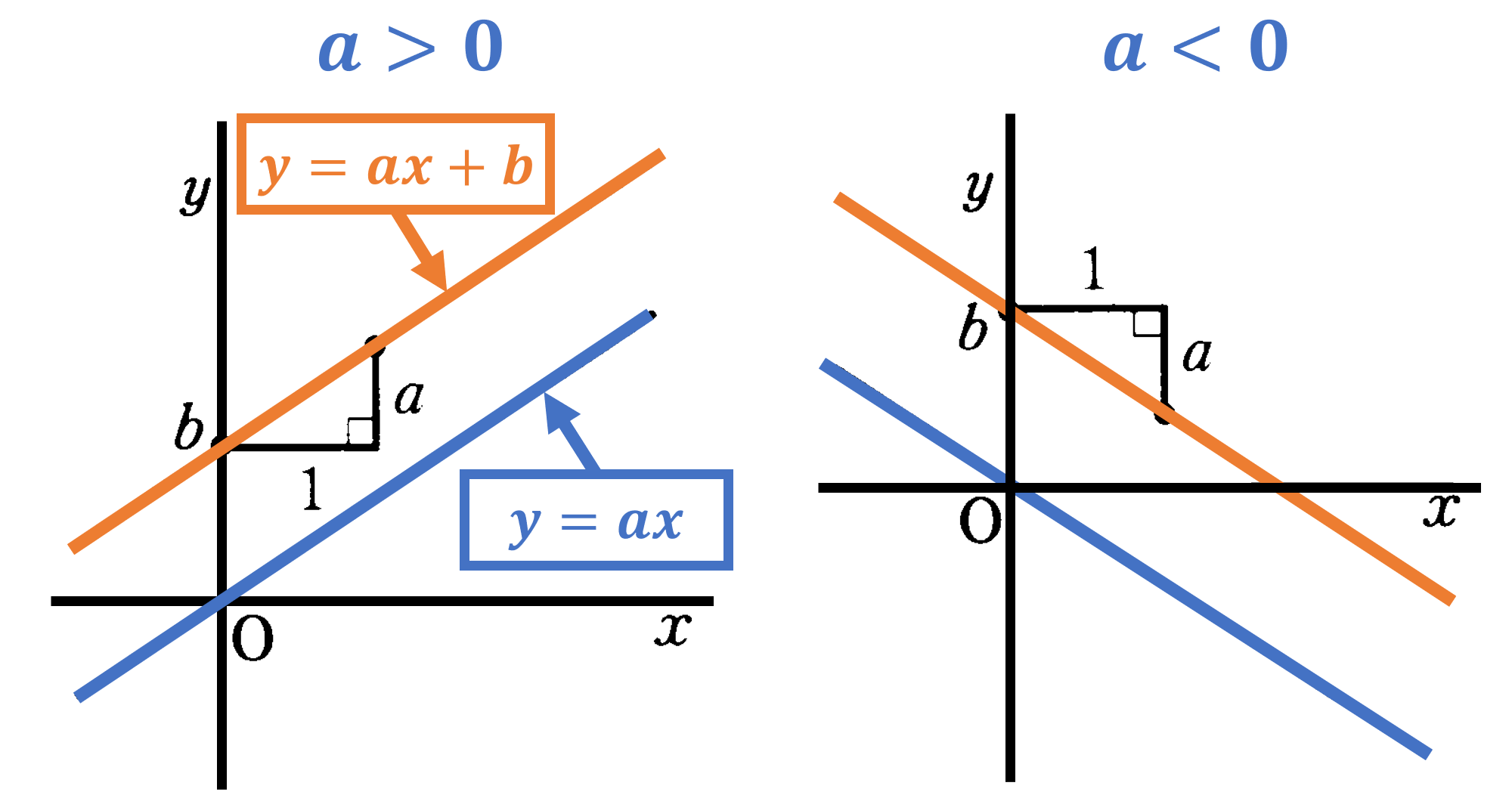
次に1次関数のグラフの特徴について考えてみましょう。比例のグラフとの関係から考えると、1次関数 $y=ax+b$ のグラフは比例の式 $y=ax$ のグラフを $y$ 軸の正の方向に $b$ だけ平行移動させた直線であると考えることができます。言い換えると、 $y=ax+b$ のグラフは点 $(0,b)$ を通り $y=ax$ のグラフに平行な直線であるともいえます。1次関数 $y=ax+b$ の定数部分 $b$ は $x=0$ のときの $y$ の値でグラフが $y$ 軸と交わる点 $(x,y)=(0,b)$ の $y$ 座標になっています($y=ax+b$ に $x=0$ を代入した時に $y=b$ となることを確認すること)。この $b$ を1次関数のグラフの切片といいます。また変化の割合である $a$ をそのグラフの傾きといいます。つまり1次関数 $y=ax+b$ のグラフは傾きが $a$ 切片が $b$ の直線であるといえます(直線を表す式 $=$ 1次関数であると考えることができます)。傾き $a$ が正の値の場合は $x$ の値が増加すれば $y$ の値も増加する「右肩上がりの直線」 $a$ が負の値の場合は $x$ の値が増加すれば $y$ の値は減少する「右肩下がりの直線」となります。1次関数とそのグラフの関係についてまとめると、変化の割合と傾きが対応し、$x,y$ の値が通る点 $(x,y)$ と対応します。この関係を利用することで、1次関数からグラフを、グラフから1次関数を、それぞれ求めることができます。練習問題に沢山触れることで1次関数の表現になれ、式からグラフをすぐにイメージできるようになりましょう。
1次関数 $y=ax+b$ の値の変化:
(1) 増加・減少: $x$ の値が増加するとき $y$ の値は $a>0$ ならば増加 $a<0$ ならば減少
(2) 変化の割合: 変化の割合 $=\frac{yの増加量}{xの増加量}=a$ (一定)
1次関数 $y=ax+b$ のグラフについて:
(1) 傾き $a$ 切片 $b$ の直線。
(2) 次の2つは等しい:(1) 直線 $y=ax+b$ の傾き $a$ $\iff$ (2) 1次関数 $y=ax+b$ の変化の割合 $a$
(3) $a>0$ のとき右上り(傾き:正) $a<0$ のとき右下り(傾き:負)。
※ 変域を求める方法:1次関数 $y=ax+b$ について $a > 0$ で $x$ の変域が $m < x < n$ のときの $y$ の変域は $am+b < y < an+b$ となる。 $a < 0$ で $x$ の変域が $m < x < n$ のときの $y$ の変域は $an+b < y < am+b$ となる。(グラフから読み取る方法も理解しておくこと)。
1次関数の式の求め方
本節では1次関数の式を求める方法を学びましょう。前節でも説明しましたが、1次関数とそのグラフの関係についてまとめると、変化の割合 $=$ 傾き、$x,y$ の値 $=$ 通る点 $(x,y)$ であるという関係を利用することで、1次関数からグラフを、グラフから1次関数を、それぞれ求めることができます。様々な条件から正しく1次関数の式を求められるよう演習に取り組みましょう。
1次関数の式の決定方法:1次関数 $y=ax+b$ の $a$ と $b$ で決まる。
(1) 通る点と傾きから決定: 傾き $a$ が分かっているため通る点から $b$ を決定する。
例
グラフの傾きが $\frac{2}{3}$ で 点 $(x,y)=(3,1)$ を通る直線の式を求める。傾きが $\frac{2}{3}$ のため求める直線の式は $y=\frac{2}{3}x+b$ である。この式に $(x,y)=(3,1)$ を代入すると $1=2+b \to b=-1$ となる。よって答えは $y=\frac{2}{3}x-1$ となる。
(2) 通る2点から決定:
解法1:2点の座標から傾き $a$ を求めた後に切片 $b$ を決定する。
例
2点 $(-1,2),(3,-4)$ を通る直線の式を求める。グラフの傾きは $a=\frac{2-(-4)}{-1-3}=\frac{6}{-4}=-\frac{3}{2}$ となる。よって求める直線の式は $y=-\frac{3}{2}x+b$ となる。この式に通る点 $(x,y)=(-1,2)$ を代入すると $2=\frac{3}{2}+b \to b=\frac{1}{2}$ となる。よって答えは $y=-\frac{3}{2}x+\frac{1}{2}$ となる。
解法2:2点の座標を $y=ax+b$ に代入し $a$ と $b$ に関する連立方程式を解く。
例
2点 $(-1,2),(3,-4)$ を通る直線の式を求める。2点の座標を $y=ax+b$ に代入すると次の連立方程式が得られる。
\begin{cases}
{}
2 = -a+b \ ―①& \\
-4 = 3a+b \ ―②&
\end{cases}
$①-②$より
\begin{eqnarray}
2-(-4) &=& -a-3a+b-b \\
6 &=& -4a \\
a &=& -\frac{3}{2}
\end{eqnarray}
この結果を$①$に代入すると
\begin{eqnarray}
2 &=& \frac{3}{2}+b \\
b &=& 2-\frac{3}{2} \\
b &=& \frac{1}{2}
\end{eqnarray}
が得られる。よって求める直線の式は$y=-\frac{3}{2}x+\frac{1}{2}$となる。
1次関数と方程式
本節では、2つの文字 $x,y$ をふくむ2元1次方程式 $ax+by=c$ ($a,b,c$ は定数とします)の表すグラフについて考えてみましょう。この方程式を成り立たせる $x,y$ の組は無数に存在し、この $x,y$ の値の座標をグラフとして描くと、直線になります。2元1次方程式 $ax+by=c$ を見やすい形に表すために $y$ について解くと $y=-\frac{a}{b}x+\frac{c}{b}$ となり、傾き $-\frac{a}{b}$ 切片 $\frac{c}{b}$ の直線であることが分かります。この直線を方程式 $ax+by=c$ のグラフといいます。このグラフは方程式 $ax+by=c$ の解を座標にもつ点の集まりでできた直線です。とくに $a=0$ の場合は $x$ 軸に平行な直線( $y=\frac{c}{b}$ )、$b=0$ の場合は $y$ 軸に平行な直線( $x=\frac{c}{a}$ )になります。ここでは説明を一般化するために $a,b,c$ を用いて説明しましたが、そこに具体的な数字を入れて、いろいろな方程式のグラフを描いてみましょう。きっと理解が深まるはずです。
続いて、2つの2元1次方程式(連立方程式)とグラフの関係について考えてみましょう。先ほど1つの2元1次方程式が直線のグラフとなることを学びました。さらに、その直線は、その方程式の解の集まりだということも学びました。これらのことから、2つの2元1次方程式をグラフにしたとき、2本の直線ができ、さらにその2直線の交点 $(p,q)$ は、2つの方程式をそれぞれ成り立たせる解、つまり連立方程式の解となることが分かります。整理すると $x,y$ についての連立方程式の解は、それぞれの方程式のグラフの交点の $x$ 座標 $y$ 座標の組となります。このようにして、グラフを活用して連立方程式を解くことができます。関数のグラフと方程式の関係を正しく理解し、問題に合った解き方ができるようになりましょう。
2元1次方程式 $ax+by=c$ のグラフについて:
(1) 直線を表す。
(2) $a \neq 0$, $b \neq 0$のとき $y$ について解くと $y=px+q$($y=-\frac{1}{b}x+\frac{c}{b}$)の形となる。 $\to$ この1次関数のグラフと一致する。
$x$軸, $y$軸に平行な直線:
(1) $y=q$ のグラフ:$x$軸に平行な直線となる。
(2) $x=p$ のグラフ:$y$軸に平行な直線となる。
$ax+by=c$ について:
$a=0$, $b \neq 0$ のとき: $by=c$ $\to$ $y=\frac{c}{b}$ の直線となる。$\frac{c}{b}=q$とすれば上(1)の例と同じグラフになる。
$a \neq 0$, $b=0$ のとき: $ax=c$ $\to$ $x=\frac{c}{a}$ の直線となる。$\frac{c}{b}=p$とすれば上(2)の例と同じグラフになる。
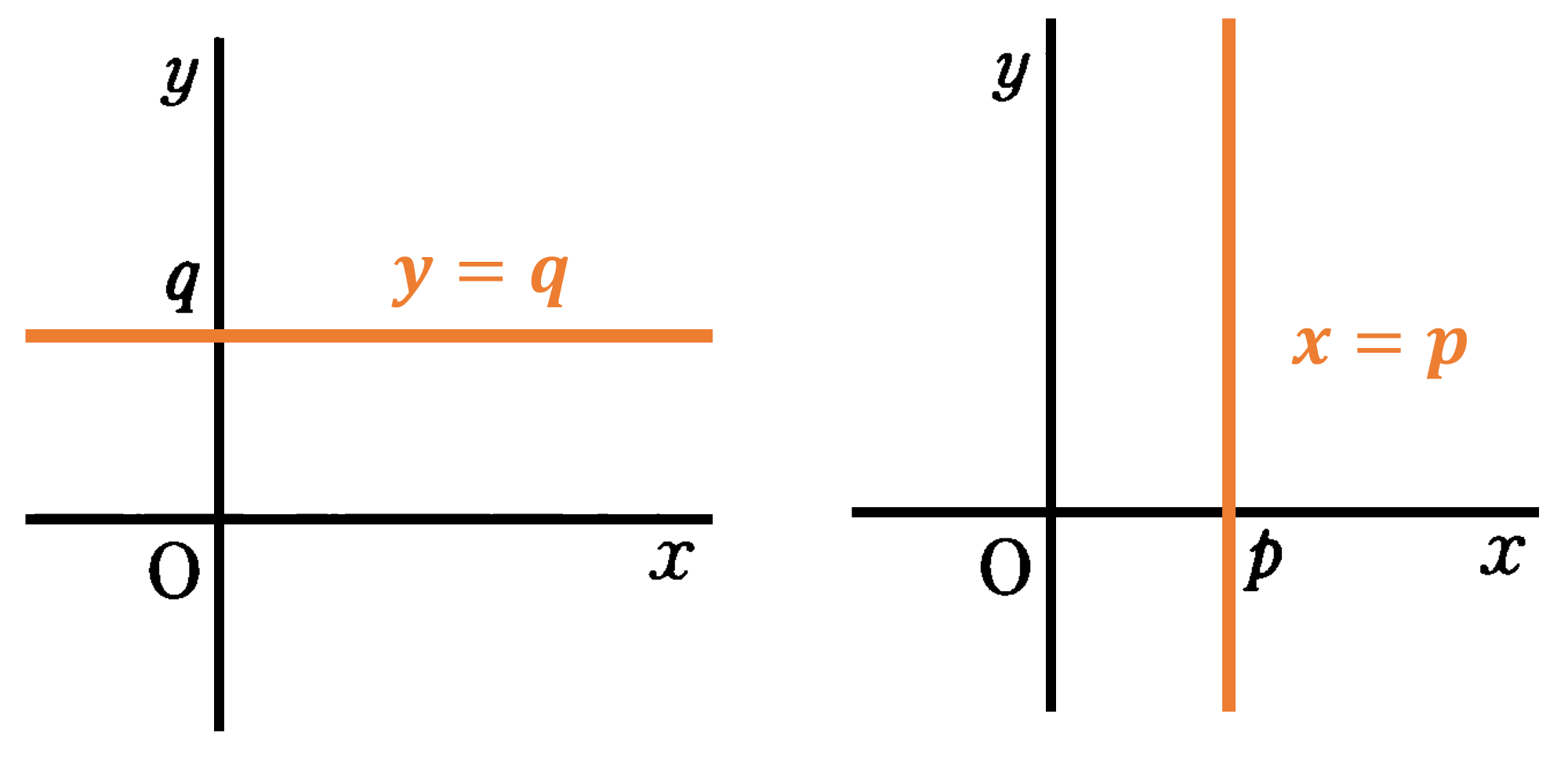
連立方程式とグラフ:
次の2つは等しい:(1) 連立方程式 $
\begin{cases}
{}
ax + by = c & \\
a’x + b’y = c &
\end{cases}
$ の解 $\iff$ (2) 2直線 $
\begin{cases}
{}
ax + by = c & \\
a’x + b’y = c &
\end{cases}
$の交点の座標
1次関数の利用
本節では1次関数を利用して問題を解決することを考えます。例えばやかんや水筒の温度の変化を調べたり、標高と気温の関係を考察したり、電車のダイヤグラムを読み取ったり、水道光熱費や携帯料金と使用量と料金の関係を調べたり、図形の面積の変化を考えたりと、ある2つの数量の間の関係を1次関数とみなして解決できる問題は無数にあります。実際に具体的な問題に取り組み、1次関数とそのグラフを活用して、問題を解決してみましょう(図形の面積を1次関数で表現する問題として「点Pが辺上を移動する」という問題はよく出題されます。いくつかのパターンを解いて理解を深めておきましょう)。
一定の速さで動く点の位置をグラフに表す:
例
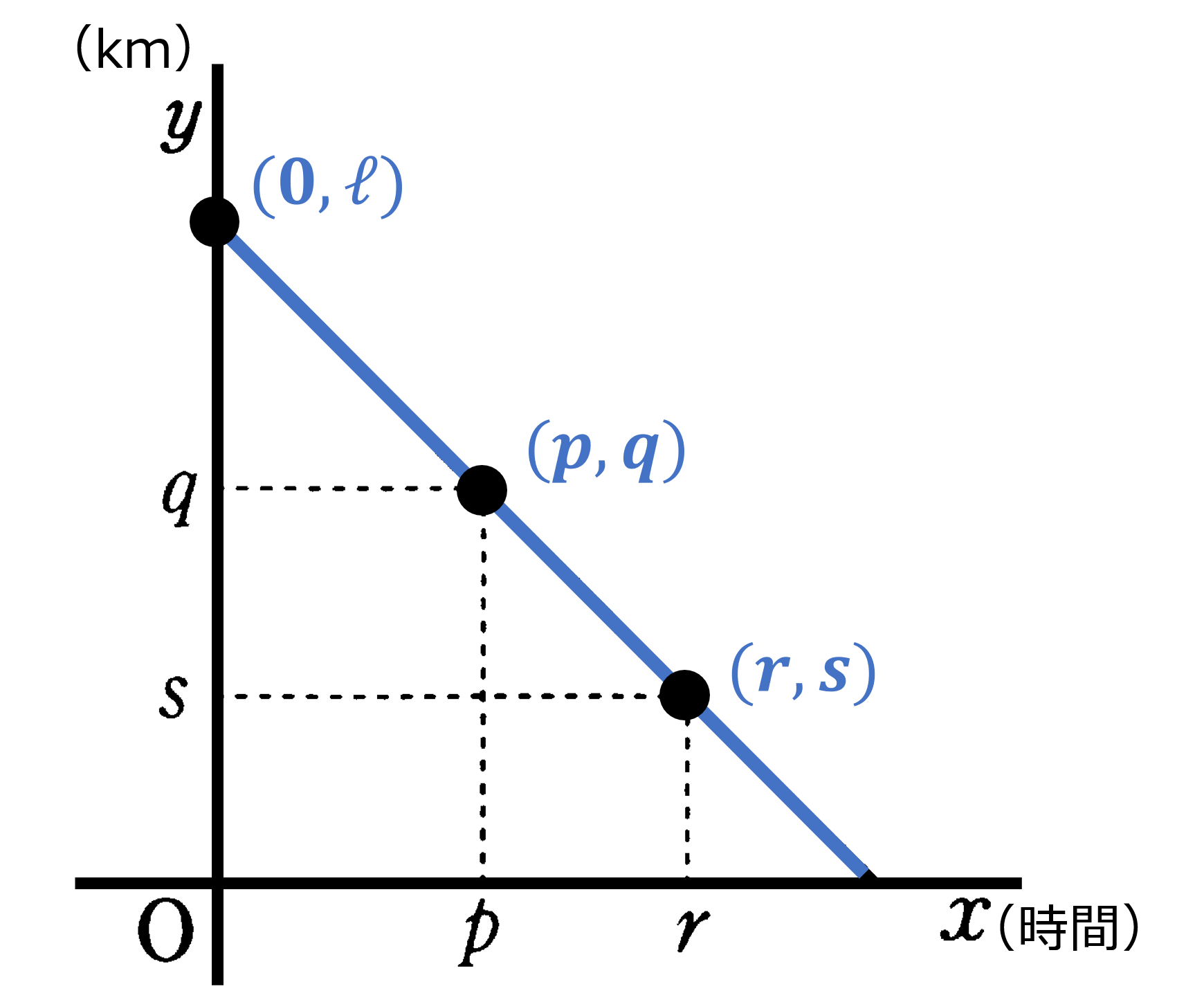
A君が$\ell$km 離れた出発点からこちら(距離0の地点)に向かって歩いている。A君は $x$ 時間後に出発点から $y$ km の距離にいるとする。このとき次の2つは等しい:
(1) $x=p$ のとき $y=a$, $x=r$ のとき $y=s$ である。$\iff$ (2) 2点 $(p,q)$, $(r,s)$ を通る。