🔄 最終更新日 2019年12月11日 by takara_semi
中1 ＞ 7章：資料の整理と活用
この章では資料を活用した身近な問題の解決方法を学びます。そのために、資料を整理する方法や、資料の傾向を読み取り判断する方法を正しく理解しましょう。
資料の整理とその活用
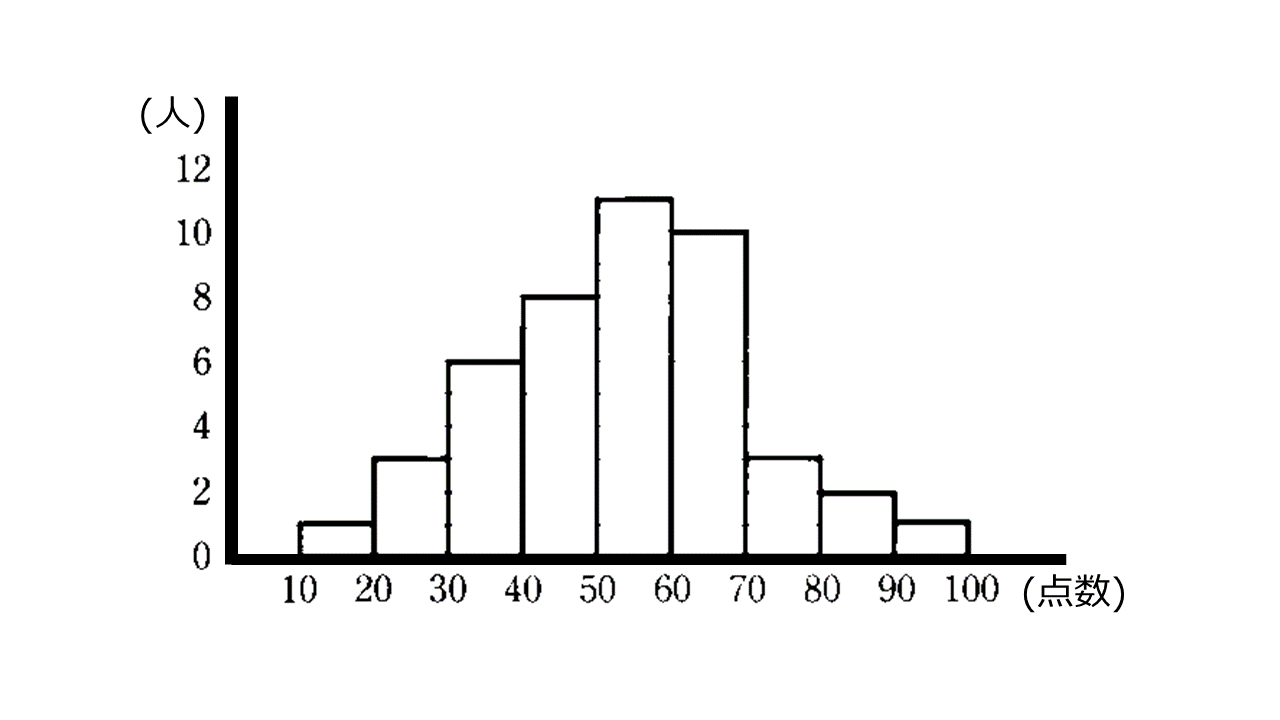
与えられた資料をどのように整理すれば、問題解決につながる特徴や傾向を得ることができるでしょうか。たとえばクラスの生徒のテストの点数の資料が与えられたとします。その資料は、$10$ 点ごとの区間に分けて、その区間に入っている人数を調べてまとめたものでした。このとき、資料を整理するために用いた区間を階級、区間の幅を階級の幅（例えば $60$ 点～ $70$ 点の階級に関してその幅は $10$ 点）、階級の真ん中の値を階級値、それそれの階級に入っている資料の個数をその階級の度数という（例えば $80$ 点～ $90$ 点の階級に $5$ 人の生徒が入っていた場合、度数が $5$ となる）。そして資料をいくつかの階級に分けて階級ごとの度数を示した表を度数分布表、特に度数分布表を柱状のグラフで表したものをヒストグラムという。また全体の度数が異なる資料を比較するときには、そのままでは分布の特徴などを正しく比べることができないので、度数の代わりに、度数の合計に対する割合である相対度数（ $\frac{その階級の度数}{度数の合計}$ ）という値を用います。相対度数を用いることで、度数の異なる資料に対して正しく分布の特徴などを比較することができます。
資料の特徴を理解したり分かりやすく伝えたりするとき、最大の値から最小の値を引いた値を用いることがあります。最大の値から最小の値を引いた値をその分布の範囲もしくはレンジといいます（範囲 $=$ 最大の値 $-$ 最小の値）。またレンジの他の分布の特徴として、分布から求められる1つの数値である代表値というものがあります。資料を比較するときには、この代表値を比べることが多くあります（主な代表値として平均値・中央値（メジアン）・最頻値（モード）などがあり、目的によって使い分けられます。平均値が多く使用されますが、外れ値（極端な数値）がある場合は中央値や最頻値が用いられることが多くなります）。
資料を正しく読み解くことができるようになると、スポーツやビジネス、医療や研究など、あらゆる場面で活躍できるようになります。本節では上述のような統計の専門用語が多く出てきますが資料の活用（統計）に関する知識は生涯活躍する非常に重要なものなので、着実に身に着けていきましょう。
数学が面白くなる動画―9
数学と物理の力を使えば世界記録をだすこともできるのです。
度数分布表：調査する資料をいくつかの階級に分けて各階級の度数を表にしたもの。
平均値：個々の資料の値の合計を資料の総数で割った値：平均値 $=$ $\{$(階級値$\times$度数)の合計$\}$ $\div$ 度数の合計
中央値（メジアン）：資料の値を大きさの順に並べた時の中央の値。資料の総数が偶数の場合は中央にある2つの値の平均値が中央値となる。
最頻値（モード）：資料の中で最も多く出てくる値。度数分布表では度数の最も多い階級の階級値。ヒストグラムの最も高い山の部分。
数学が面白くなる動画―10
少子化が進むと将来日本から子供はいなくなるのでしょうか？人口のヒストグラム（人口ピラミッド）を活用して未来予想をしてみましょう。
数学が面白くなる動画―11
1000人中900人が助かる病院Aと800人が助かる病院Bがあるとき、どちらの病院が、いい病院でしょうか？統計データはいつも正しい結果をあたえてくれるのでしょうか？
近似値と有効数字
$1$ と $1.00$ とでは何か違いがあるのでしょうか。例えば地球の大きさは半径「約 $6378$ km」で太陽からの距離は「約 $149600000$ km」です。$6378$ kmという数字には全て意味がありそうですが、$149600000$ kmという数字は、どこまで正確に測定された距離なのでしょうか。ここで有効数字という考え方を導入すると、地球と太陽の距離は有効数字を $4$ 桁と仮定すると $1496 \times 10^5$ kmと表すことができ、見やすく、そして数字の意味も分かりやすくなります。本節では、このような数字の表示の決まりや意味について理解しましょう。
近似値：真の値ではないが、それに近い数。例えば四捨五入した数など。はかりやものさしなどの計器では、最小の目もりの $\frac{1}{10}$ を目分量で読み取り四捨五入した値を用いることが多いが、これも近似値であると考えることができる。
誤差：誤差 $=$ 近似値 $-$ 真の値
例
四捨五入すると $10$ になったある数 $a$ は $9.5≦a<10.5$ の範囲にある。従って、この場合の誤差の絶対値はどんなに大きくても $0.5$ であることがいえる（誤差 $=$ 10 $-$ 真の値($9.5～10.5$) のため）。
有効数字：測定によって得られた数字のうちで信頼できる数字。
例
$100$ g単位の計量器で計測した時 $2400$ gだと分かった時の有効数字は $2$ と $4$ の $2$ 桁となる（千の位の $2$ と百の位の $4$ は測定された意味のある数として信頼できる「有効な数」であるが、十の位と一の位の $0$ は単に位を示しているだけで、$0$ と計測されたわけではなく信頼できない）。どこまでが有効数字かを明確に示すためには $2.4 \times 10^3$ gのように、（整数部分が1桁の数） $\times$ （$10$の累乗）の形で表記すると分かりやすい。
＜参考文献＞
[1] “チャート式基礎からの中学1年数学―新学習指導要領準拠”, チャート研究所 数研出版 (2016)．
