🔄 最終更新日 2019年12月11日 by takara_semi
中1 > 6章:空間図形
本章では図形の見方を「平面の世界(2D)」から「空間の世界(3D)」に変えて考えてみます。身の周りには形に着目すると様々な立体としてみることができるものがあります。たとえば四角いビルは直方体、電信柱は円柱、バレーボールは球として分類することができます。世の中にはどのような形があるかを学び、その特徴について考えていきましょう。
数学が面白くなる動画―8
空間上の位置(地図の上では座標 $(x,y)$ )を正確に測定するGPSのしくみ。
いろいろな立体
いろいろな立体を比べて、その共通点や違いについて考えましょう。たとえば、平面だけで囲まれた立体は多面体と呼ばれます。多面体は、その面の数によって、四面体や八面体などといいます。他にも角柱や角錐、円錐や正多面体など、様々な立体があり、それぞれ特徴があります。その特徴と立体の名前を正しく理解し、空間図形の理解の基礎知識をしっかりと身につけましょう。
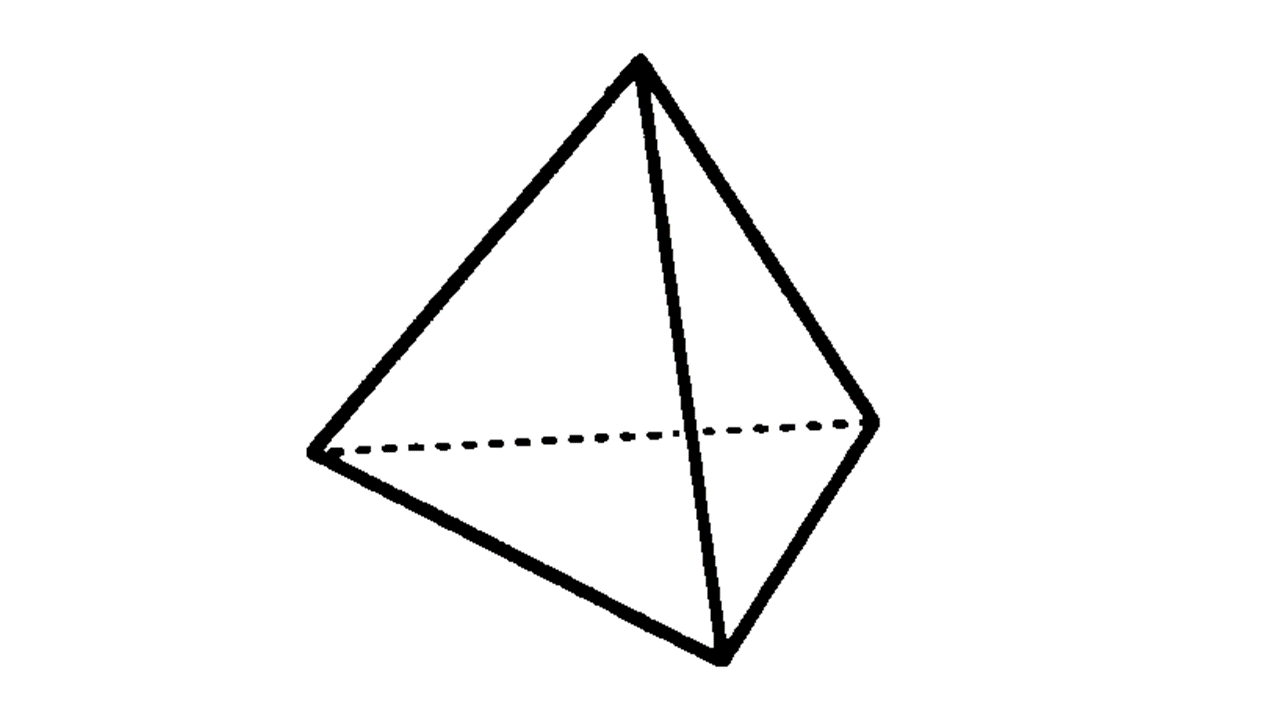
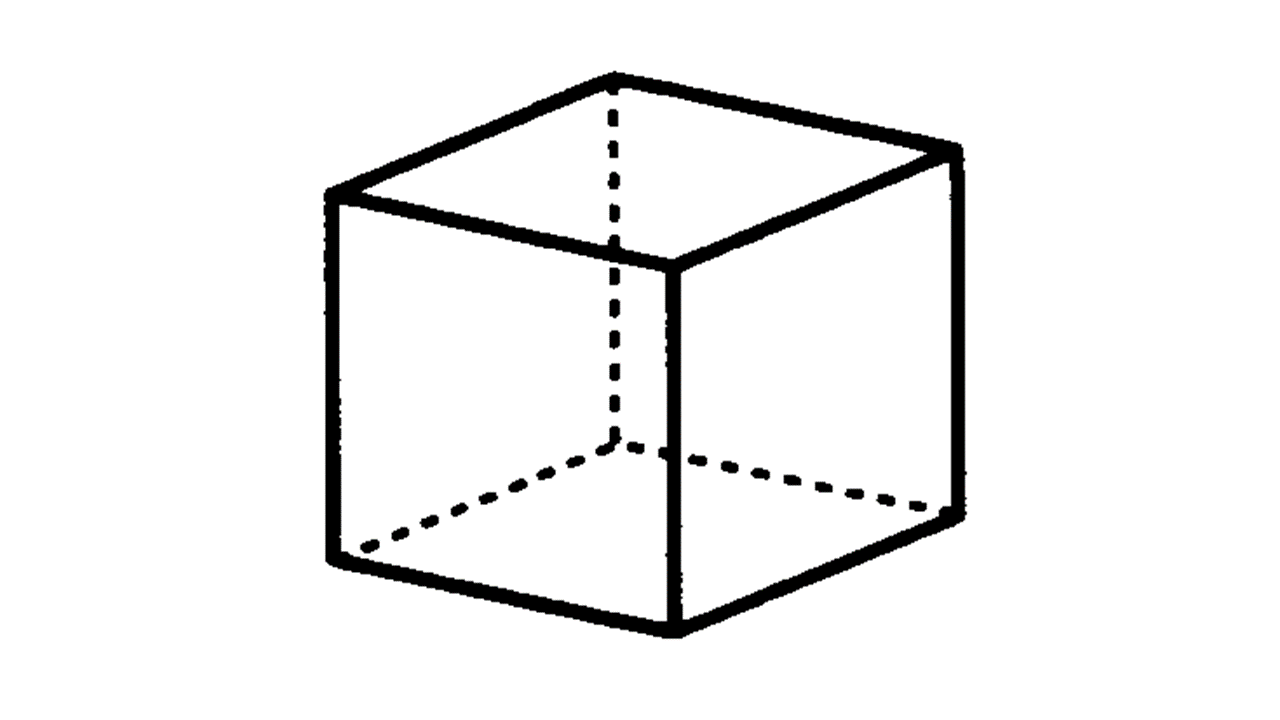
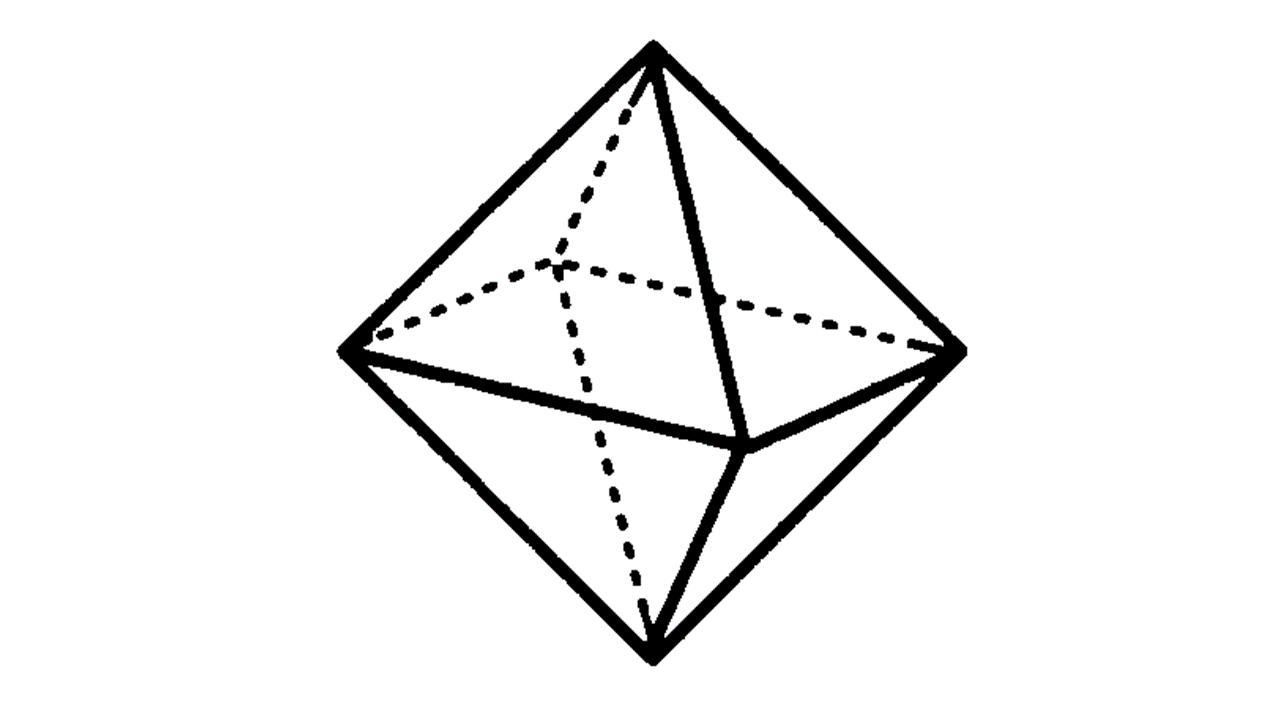
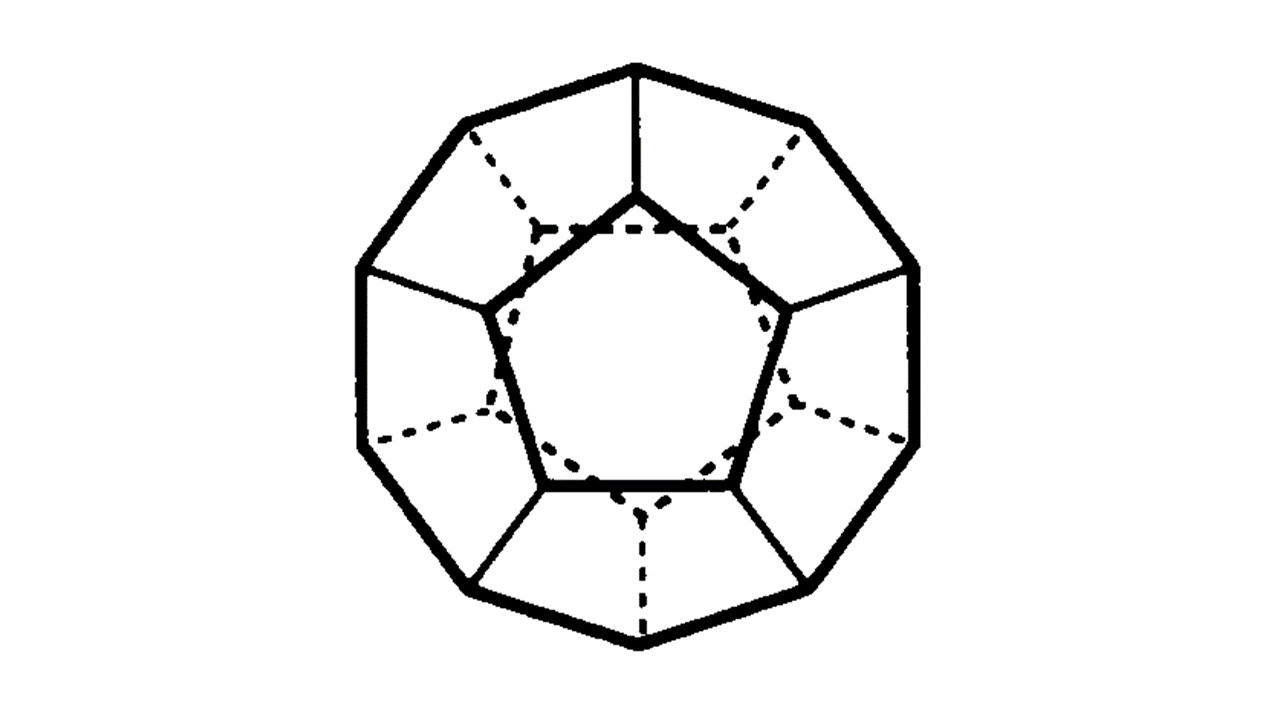
正多面体:どの面もすべて合同な正多角形であり、どの頂点にも面が同じ数だけ集まっている、へこみのない多面体。正四面体・正六面体(立方体)・正八面体・正十二面体・正二十面体の5種類。
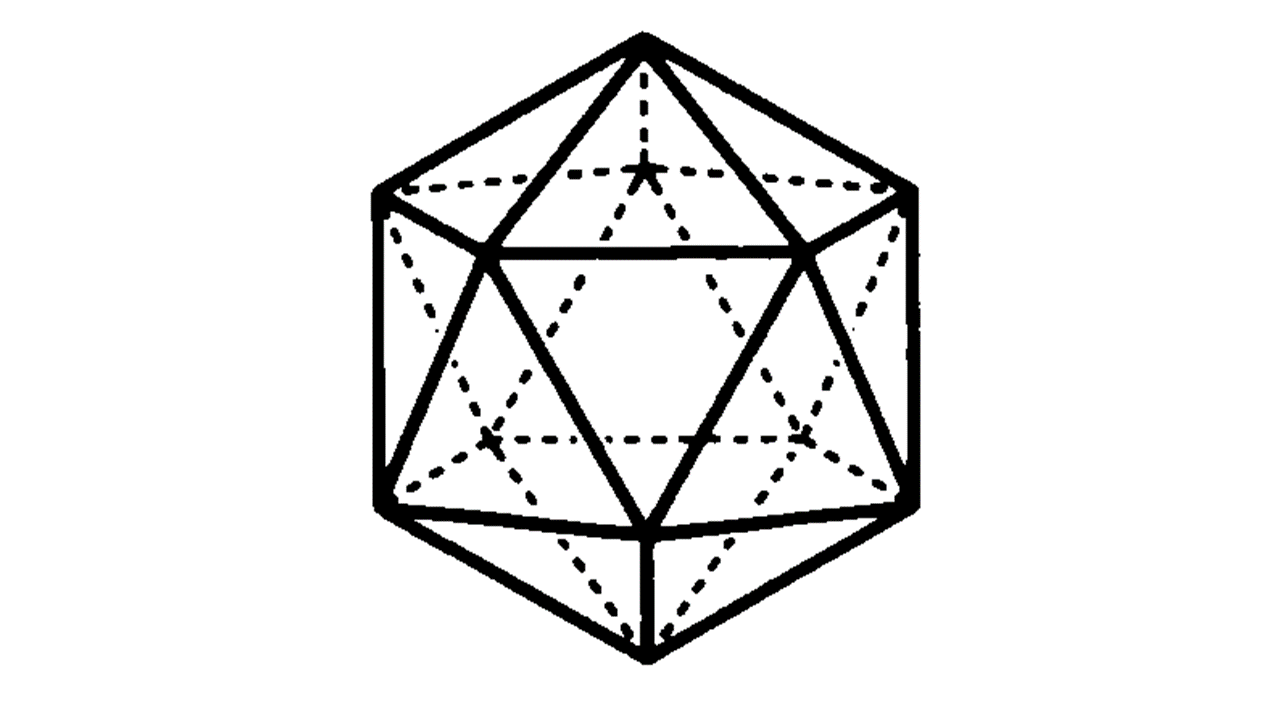
角柱・角錐・円柱・円錐
(1) 角柱:柱状で、底面が三角形の場合は三角柱、四角形の場合は四角柱、長方形(もしくは正方形)のときは直方体となる。底面が正方形で高さが正方形の1辺の長さに等しい場合は立方体となる。また、底面が正三角形で側面がすべて合同な長方形である角柱を正三角柱、底面が正方形で側面がすべて合同な長方形である角柱を正四角柱という。
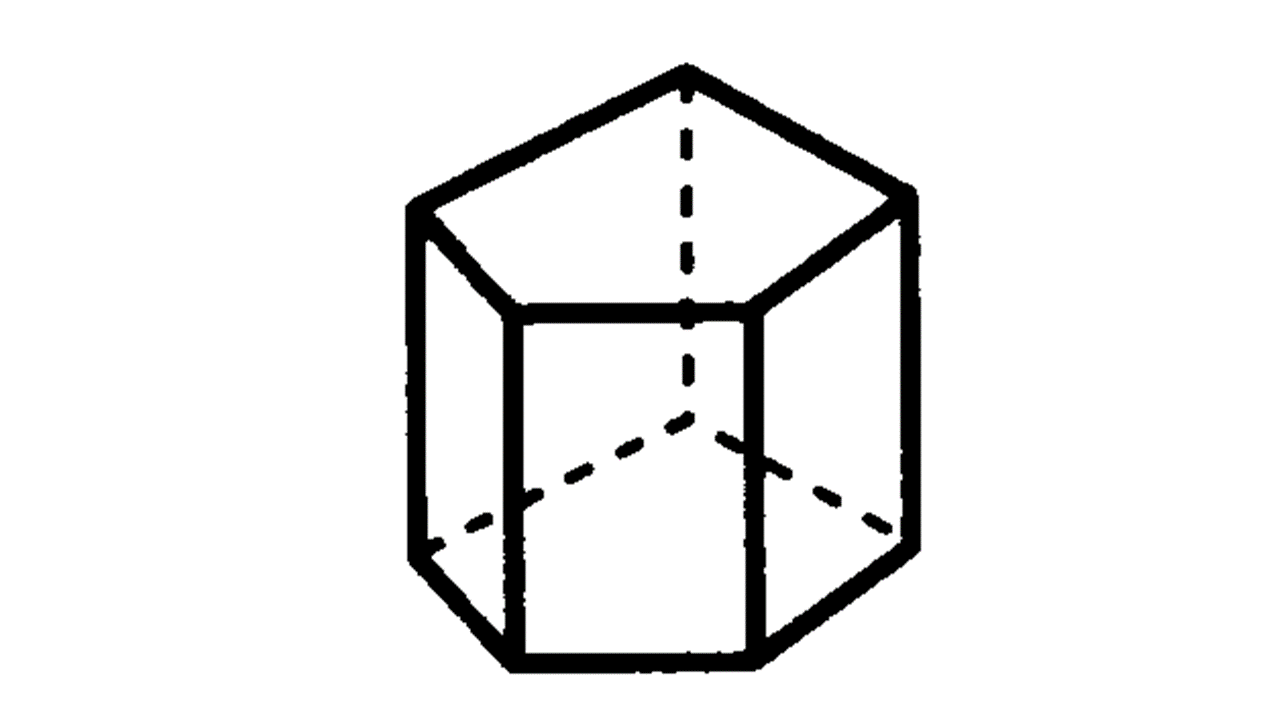
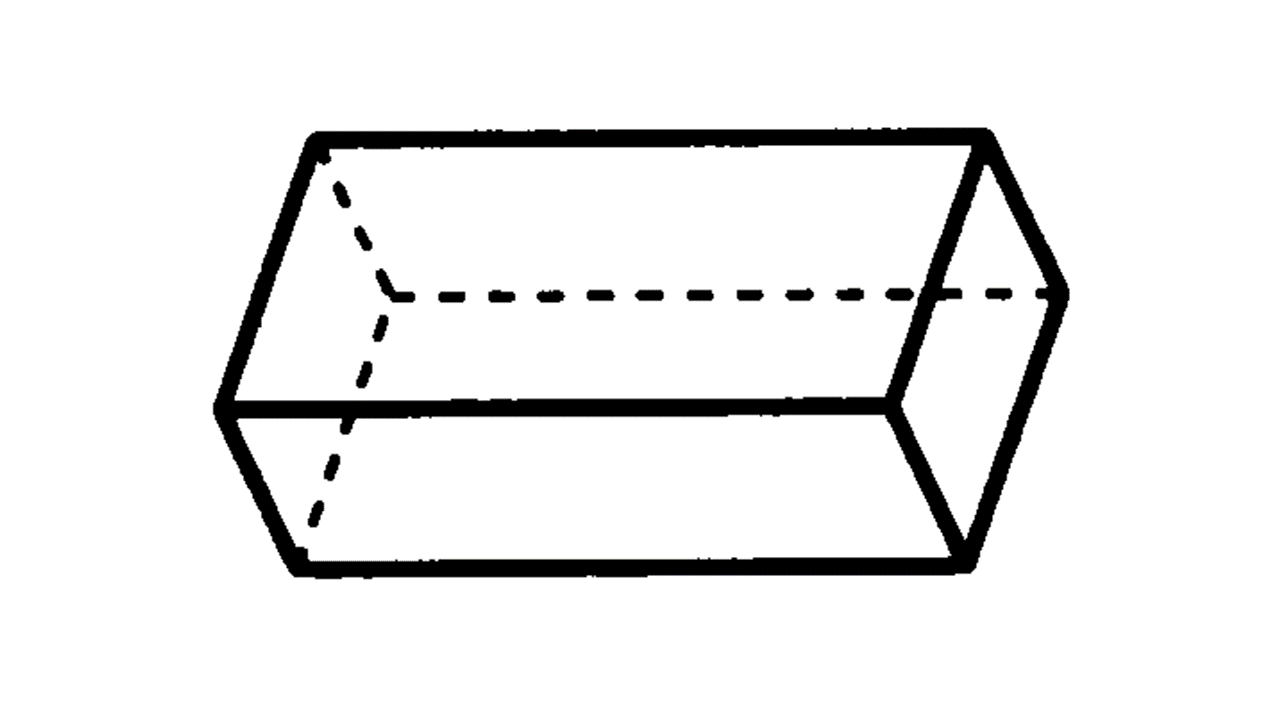
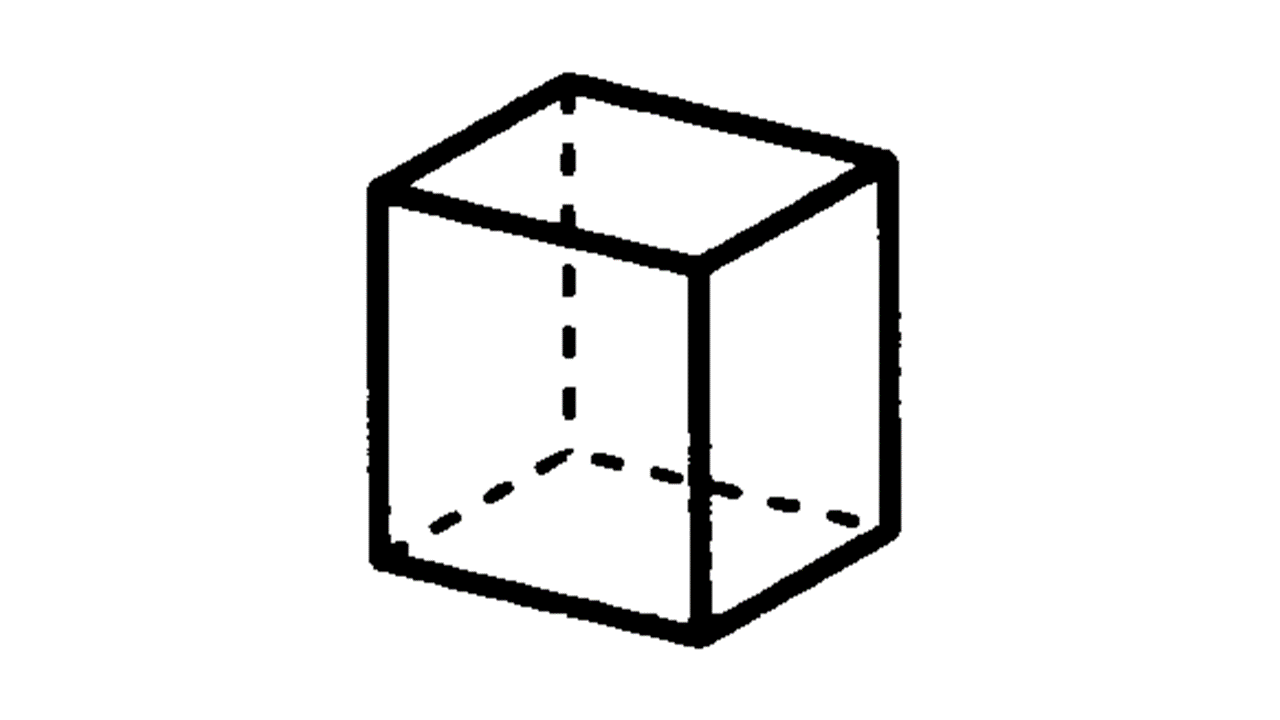
(2) 角錐:底面が三角形の場合は三角錐、四角形の時は四角錐となる。また、底面が正三角形で側面がすべて合同な二等辺三角形である角錐を正三角錐、底面が正方形で側面がすべて合同な二等辺三角形である角錐を正四角錐という。
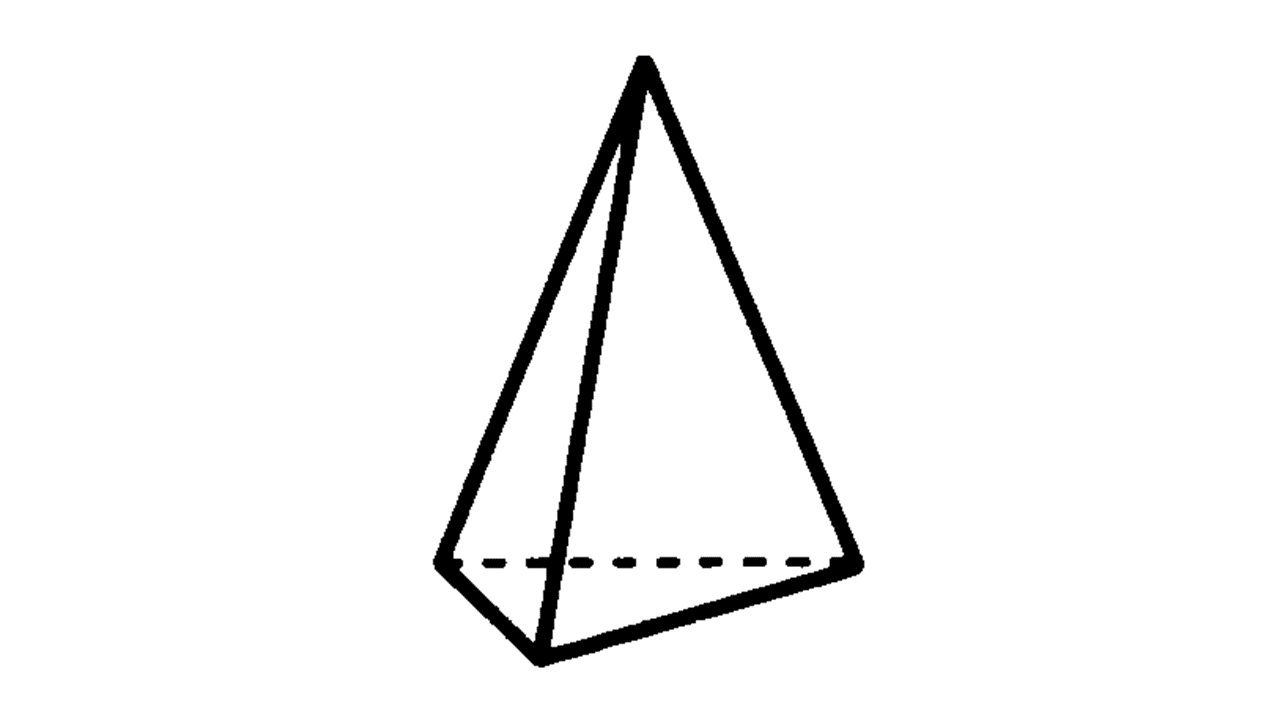
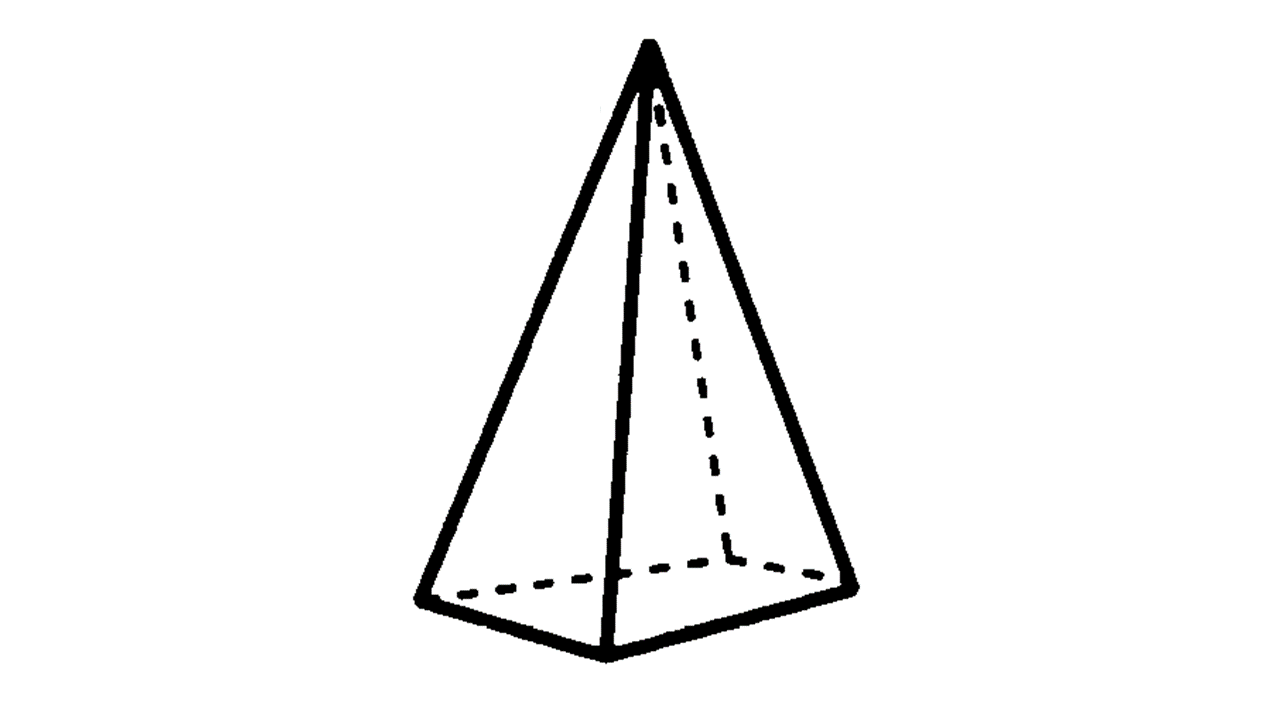
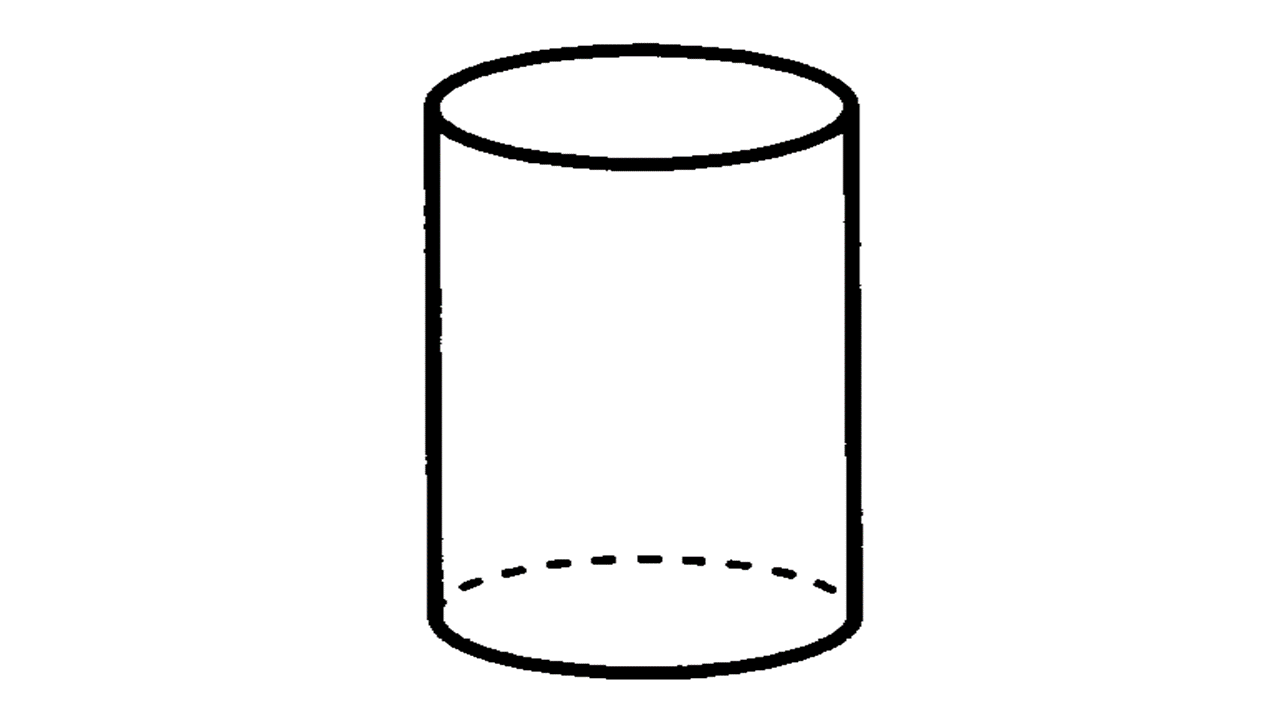
(3) 円柱:柱状で底面が円になっている立体を円柱という。
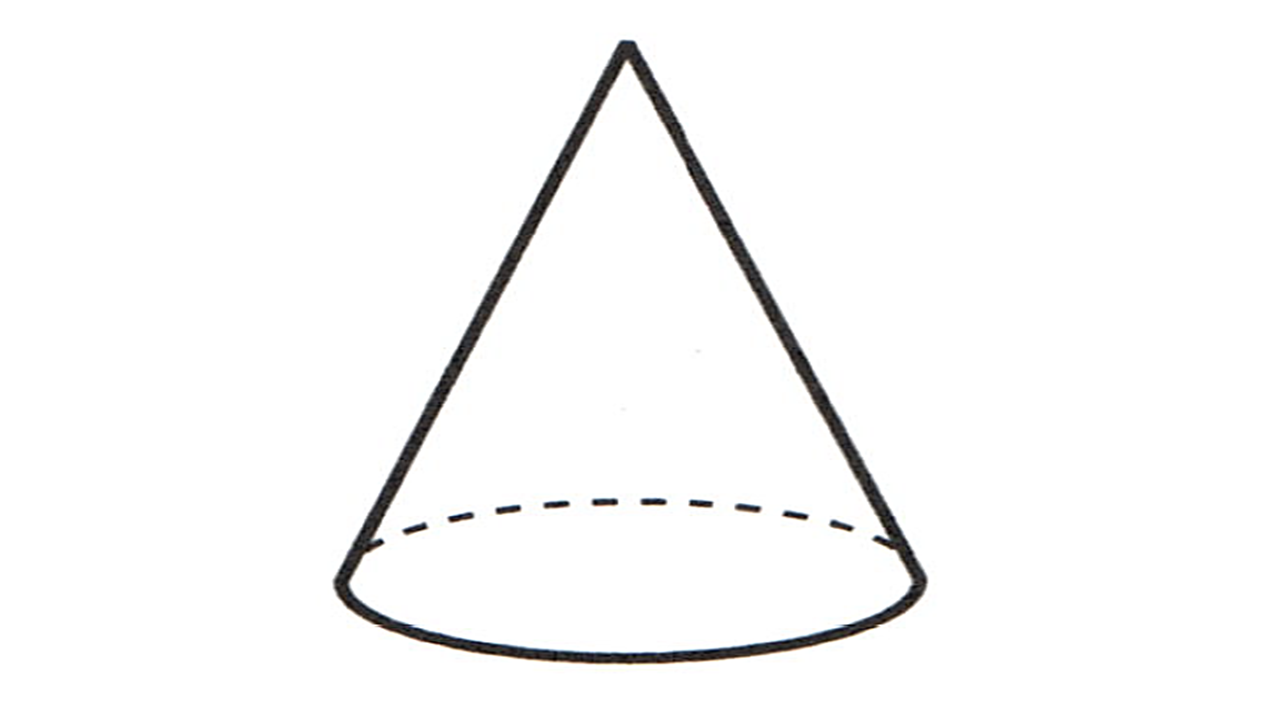
(4) 円錐:底面が円になっている錐体(※数学用語)を円錐という。
※ おまけ:オイラーの多面体定理:多面体の面や辺や頂点の数を計算するときに利用できる公式。多面体の「頂点」「辺」「面」の数について (頂点の数) $-$ (辺の数) $+$ (面の数) $=2$ が成り立つ。
直線や平面の位置関係
空間図形をとらえたり表現したりするためには、それをどの方向から見ているかなどの「位置関係」を明らかにする必要があります。そのために、空間における直線や平面の位置関係について考えてみましょう(ここでいう平面とは、両方に限りなく伸びている直線のように、限りなく広がっているものを考えます)。
平面の決定:以下の(1)~(4)のいずれかが空間に存在するときそれらを含む平面は1つに定まる。
(1) 同じ直線上にない3点。
(2) 交わる2直線。
(3) 平行な2直線。
(4) 1直線とその上にない1点。
2直線の位置関係:空間内にある2つの直線は、交わる場合と交わらない場合がある(平面図形では、交わらない2つの直線は平行である)。空間内で平行でなく交わらない2直線はねじれの位置にあるという。以上のことより2直線の位置関係は以下の(1)(2)のいずれかで表される。
(1) 同じ平面上にある $\to$ (A) 交わる。 (B) 平行である。
(2) 同じ平面上にない $\to$ ねじれの位置にある。
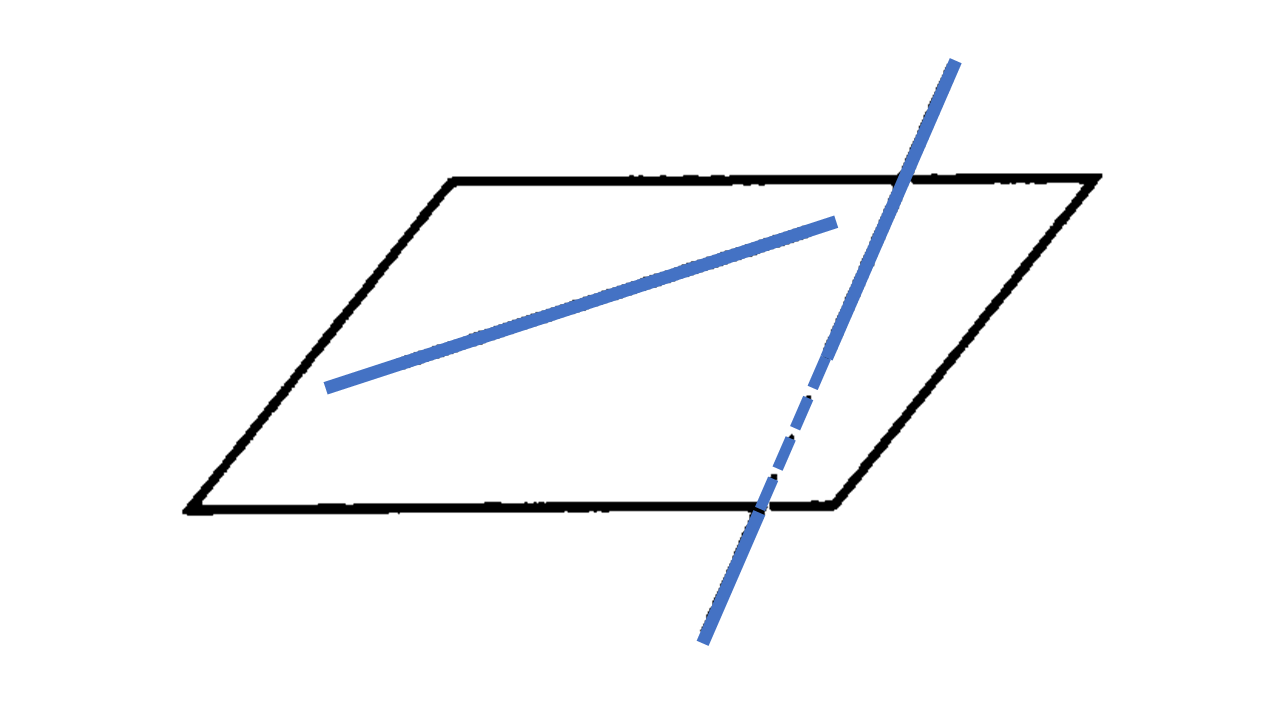
直線と平面の位置関係:直線と平面の位置関係は以下の(1)~(3)のいずれかで表される。
(1) 直線が平面に含まれる。直線が平面上にあるともいう。
(2) 1点で交わる。
(3) 交わらない(直線を $\ell$ 平面を ${\rm P}$ とすると $\ell/ \! \! /{\rm P}$)。
2平面の位置関係:平面と平面が交わったところにできる線は直線となり、この線を交線という。2平面の位置関係は以下の(1)(2)のいずれかで表される。
(1) 交わる。
(2) 交わらない(平行である。2つの平面をそれぞれ ${\rm P,Q}$ とすると ${\rm P}/ \! \! /{\rm Q}$)。
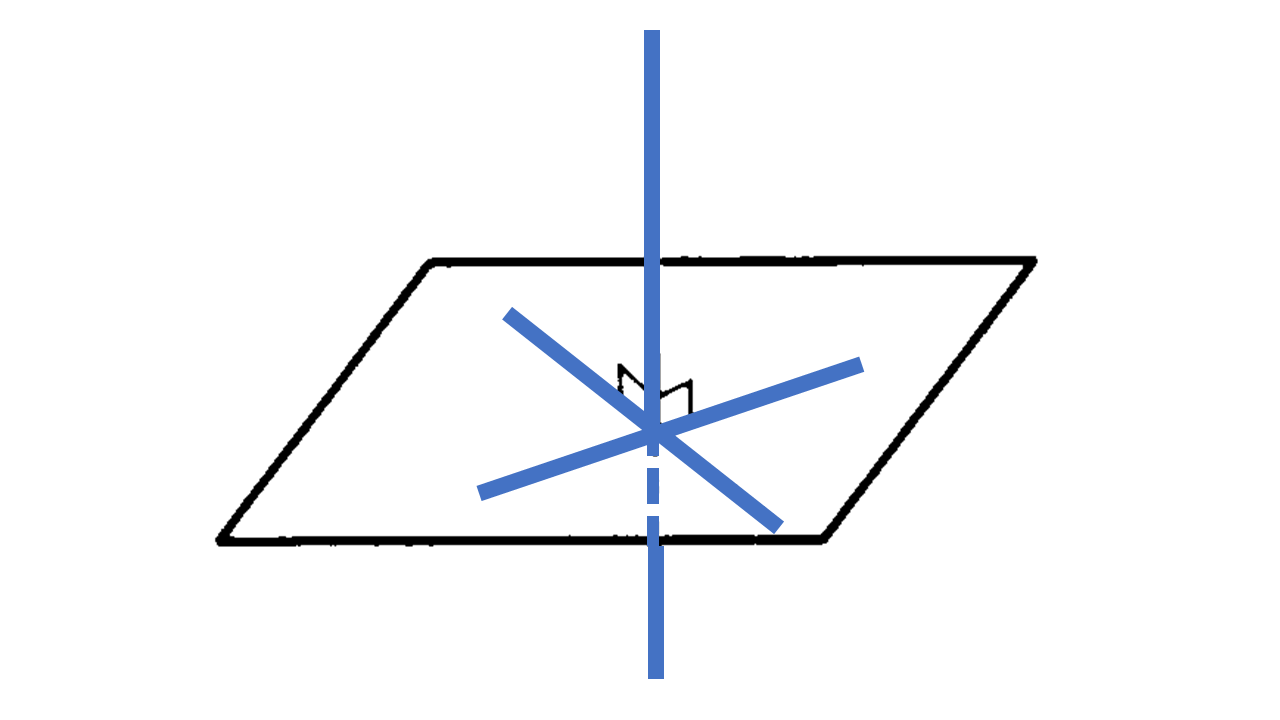
直線と平面の垂直:平面 ${\rm P}$ に対してどの方向にも傾いていない直線 $\ell$ を考える。このとき $\ell$ は ${\rm P}$ との交点 ${\rm O}$ を通る ${\rm P}$ 上のどの直線にも垂直になっている。このようなとき、直線 $\ell$ は平面 ${\rm P}$ に垂直であるという(垂直が成り立つ最小の条件としては、平面 ${\rm P}$ と交わる直線 $\ell$ がその交点 ${\rm O}$ を通る ${\rm P}$ 上の2つの直線 $m,n$ に垂直になっていれば、直線 $\ell$ は平面 ${\rm P}$ に垂直であるといえる)。
点と平面との距離:1つの点 ${\rm A}$ から平面 ${\rm P}$ に引いた垂線と、平面 ${\rm P}$ との交点を ${\rm H}$ とするとき、線分 ${\rm AH}$ の長さを点 ${\rm A}$ と平面 ${\rm P}$ との距離という。
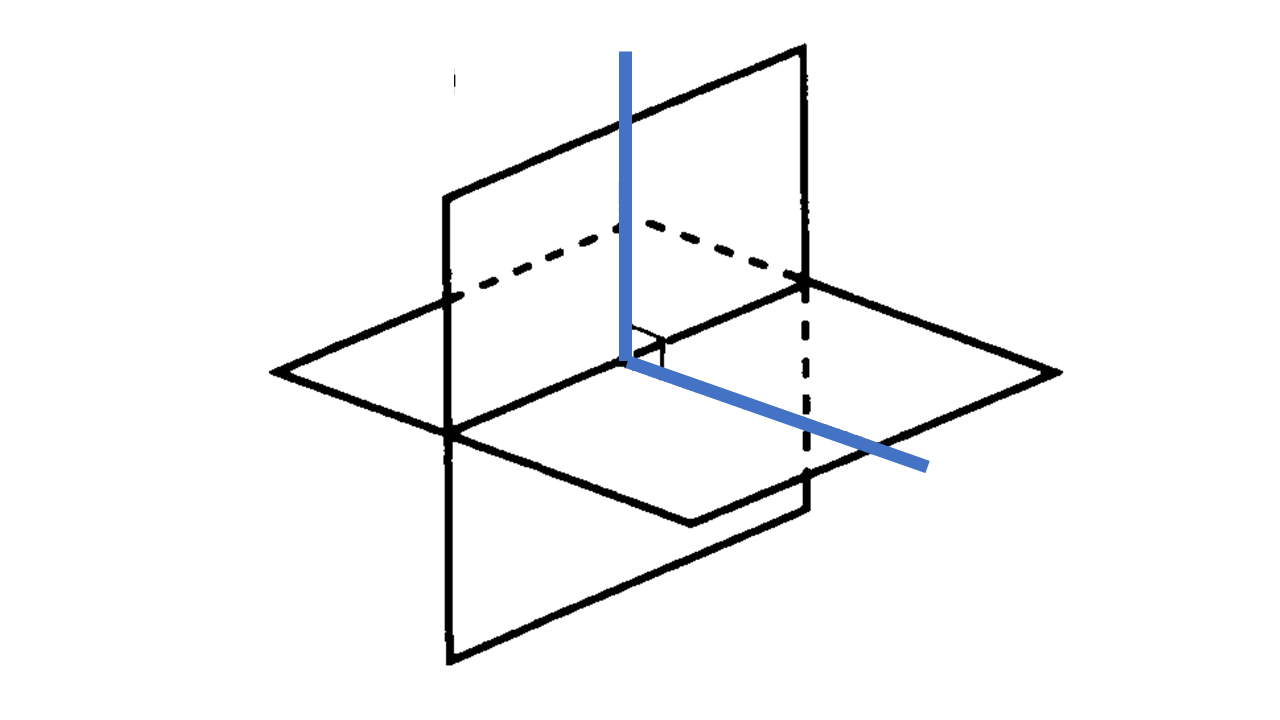
2平面の垂直:2つの平面 ${\rm P,Q}$ が交わり、この交線 $\ell$ とするとき、 ${\rm P}$ と ${\rm Q}$ のつくる角を考える。平面 ${\rm P,Q}$ のつくる角は、その交線 $\ell$ 上の点で、それぞれの平面上に引いた2つの垂線のつくる角のことである。特に、2つの平面 ${\rm P,Q}$ のつくる角が直角の時、その2つの平面 ${\rm P,Q}$ は垂直であるといい ${\rm P} \perp {\rm Q}$ と表す。
立体の構成
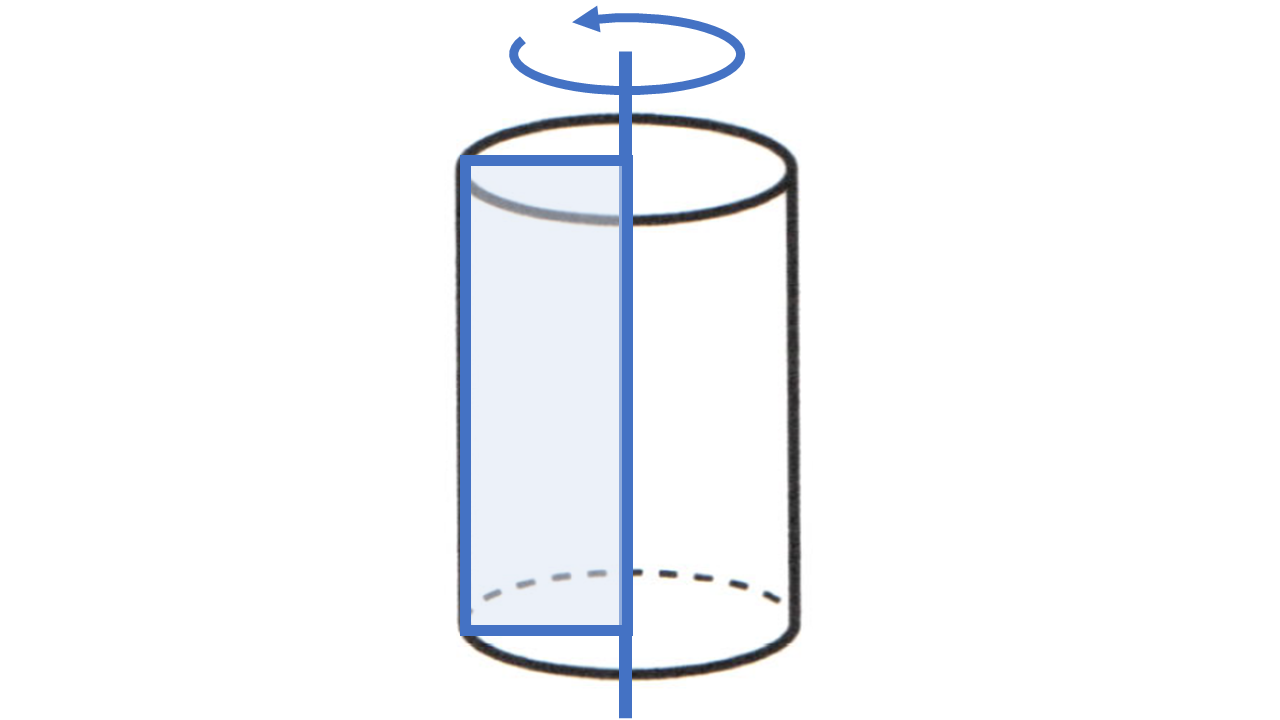
本節では、空間図形を「面の移動」という見方で見ていきます。例えば点が動くことによって線ができ、線が動くことによって面ができます。さらに、面が動くときに立体ができます。特に、円柱や円錐は、それぞれ長方形や直角三角形を「回転させてできた立体」だと考えることができます。このとき、円柱や円錐の側面を描く辺を母線といいます。また円柱や円錐のように、1つの直線を軸として平面図形を回転させてできる立体を回転体といいます。球は半円をその直径を回転の軸として回転させた回転体だと考えることができます。他にも、立体の展開図の特徴を理解することで、より深く空間図形について考えていきましょう。
回転体:
(1) 円柱:回転させる図形 $\to$ 長方形:回転の軸 $\to$ 1辺
(2) 円錐:回転させる図形 $\to$ 直角三角形:回転の軸 $\to$ 直角をはさむ辺
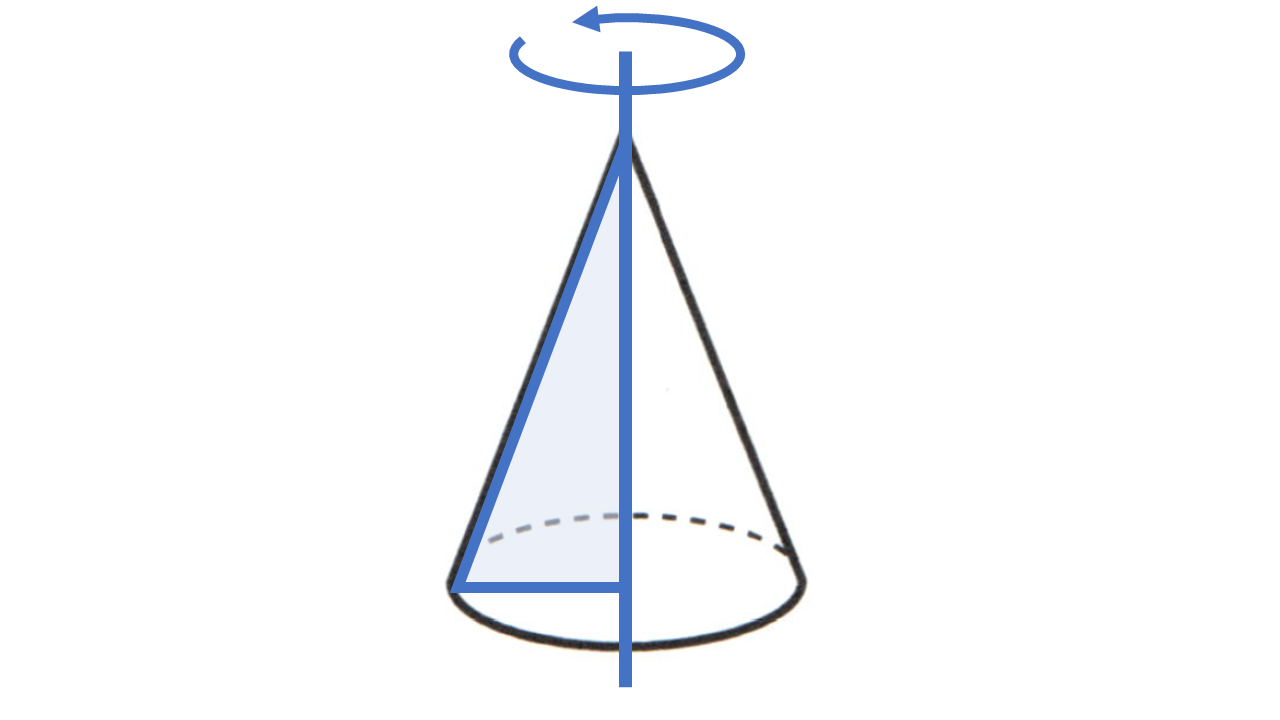
(3) 球:回転させる図形 $\to$ 半円:回転の軸 $\to$ 直径
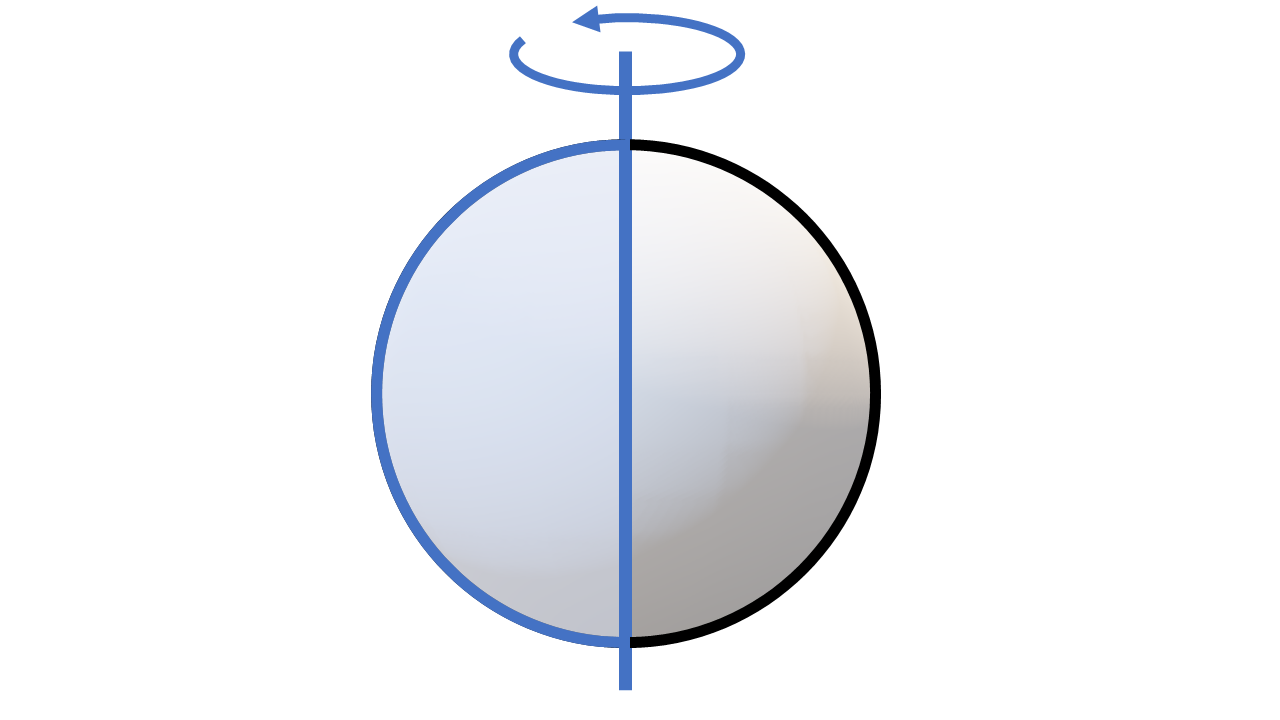
回転体の性質:
(1) 回転の軸に垂直な平面で切ると切り口は円となる。
(2) 回転の軸を含む平面で切ると切り口は回転の軸について対称な図形になる。
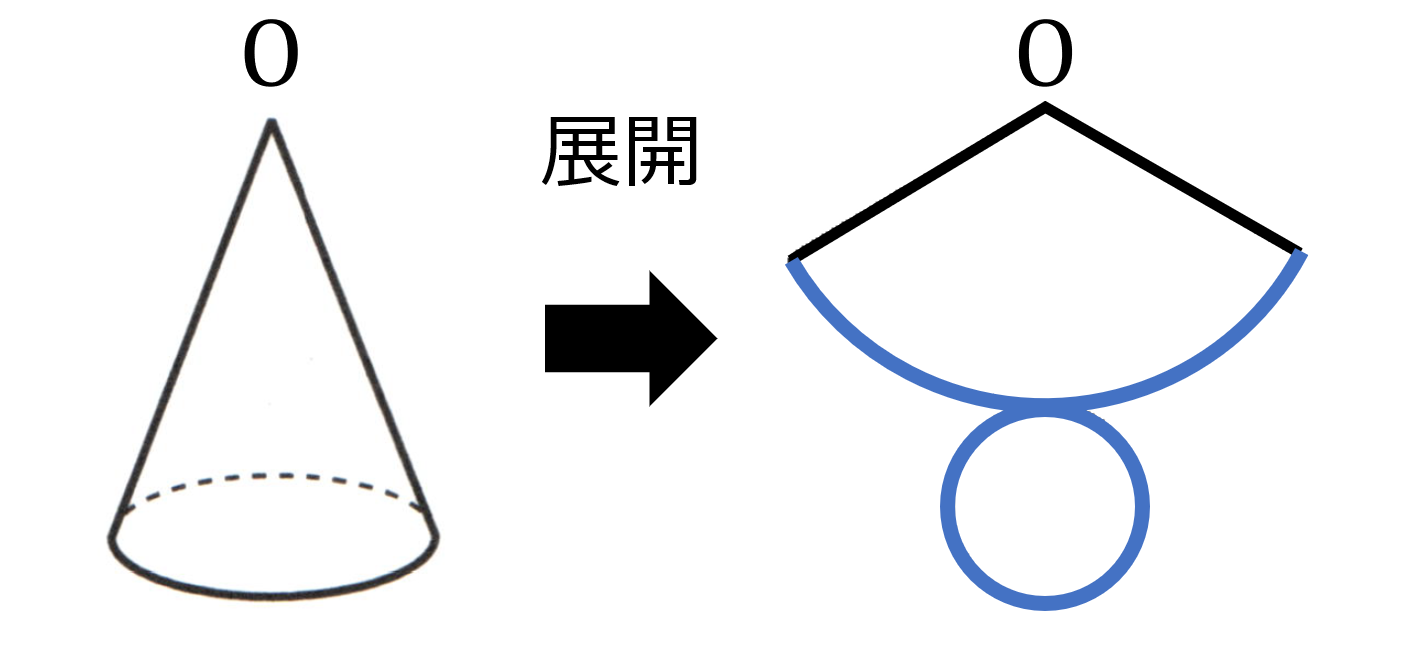
立体の展開図:立体の展開図では、立体でのすべての辺や面積の形や大きさが表現される。特に特徴的なのが円錐の展開図である。円錐の展開図は側面がおうぎ形、底面が円となる。おうぎ形の弧の長さは底面の円周に等しい。また、おうぎ形の半径は円錐の母線に等しい。
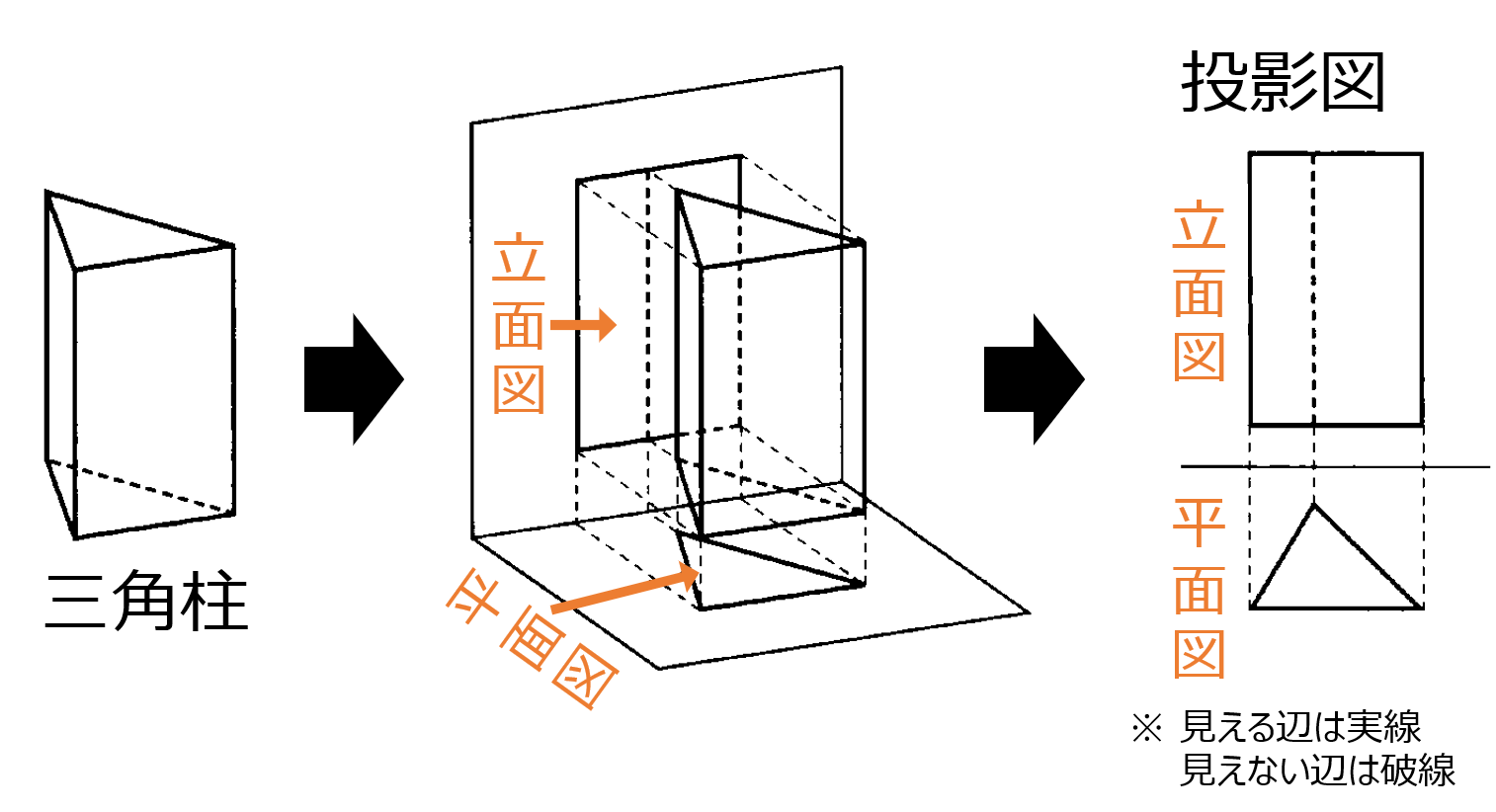
立体の投影図:立体を平面としてあらわす方法の一つ(他に見取りや展開図等がある)。立体をある方向から見て平面に表した図を投影図という。立体を真上から見た図を平面図、正面から見た図を立面図といい、立体を投影図で表現する場合、平面図と立面図を用いて表すことが多い(立体の形が読み取れない場合は横から見た図を加えることもある)。
立体の表面積と体積
例えば牛乳パックの多くは直方体、コップは円柱、パフェなどの容器は円錐などの立体としてみることができます。本節では、身の周りの容器(立体)の容積(体積)や表面積などを求める方法について考えましょう。
表面積:立体の全ての面の面積の和を表面積という。また側面全体の面積を側面積、1つの底面の面積を底面積という。
(1) 角柱・円柱の表面積 $=$ 底面積 $\times 2 +$ 側面積
(2) 角錐・円錐の表面積 $=$ 底面積 $+$ 側面積
※ おうぎ形の面積:円錐の表面積の計算でおうぎ形の面積の計算が必要になる。半径 $r$ 弧の長さ $\ell$ のおうぎ形の面積 $S$ は $S=\frac{1}{2} \ell r$ で求められる(おうぎ形を細長いおうぎ形に細かく分けたもののうちの半分を逆さまにして組み合わせると、2辺の長さがそれぞれ $\frac{1}{2} \ell$, $r$ の長方形になることから確認できる)。
(3) 半径 $r$ の球の表面積 $S$ $=$ $4 \pi r^2$
※ 球の表面積はその球がちょうど入る円柱の側面積と等しい。球の半径を $r$ とすると、その球がちょうど入る円柱は、底面の円周 $2 \pi r$ 高さ $2r$ である。よってその円柱の表面積は $S’=4 \pi r^2$ となる。このことから、球の体積が $S=S’=4 \pi r^2$ となることが確かめられる
体積:
(1) 角柱・円柱の体積 $V$ $=$ 底面積 $S$ $\times$ 高さ $h$ つまり $V=Sh$
(2) 角錐・円錐の体積 $V$ $=$ $\frac{1}{3}$ $\times$ 底面積 $S$ $\times$ 高さ $h$ つまり $V=\frac{1}{3}Sh$
※ $\frac{1}{3}$ をかけると角錐・円錐の面積が求められる理由:一例として、立方体を対角線によって6等分したものを考えることで、角錐の体積が $V=\frac{1}{3}Sh$ となることを確かめられる。円錐についても、丸暗記ではない理解の仕方をしておくと納得して計算ができる(高校数学の「積分」の知識を使うと計算ができるが、中学数学では「円錐のグラス3杯分が同じ底面積・高さの円柱のグラス1杯分と等しくなる」ことなどを実験で確認しておけば十分に理解が深まる)。
(3) 半径 $r$ の球の体積 $V$ $=$ $\frac{4}{3} \pi r^3$
※ 球の体積は、その球がちょうど入る円柱の体積の $\frac{2}{3}$ である。球の半径を $r$ とすると、その球がちょうど入る円柱は、底面積 $\pi r^2$ 高さ $2r$ である。よってその円柱の体積は $V’=2 \pi r^3$ となる。このことから、球の体積が $V=\frac{2}{3}V’=\frac{4}{3} \pi r^3$ となることが確かめられる(高校数学の「積分」の知識を使うと球の体積の計算式を厳密に証明することも可能)。

