🔄 最終更新日 2019年12月11日 by takara_semi
中1 > 5章:平面図形
この章では合同や対称という見方で平面の図形の性質を調べたり、図形を移動させたり、正確な図形を作図する方法などについて学びます。また様々な図形に触れて、その性質について理解を深めましょう。そうすることで、身近な模様に対する新たな見方もできるようになり、数学の世界の広がりを感じることができるでしょう。
数学が面白くなる動画―6
実はすごい六角形の秘密。ハチの巣はなぜ六角形なのでしょうか?
数学が面白くなる動画―7
なぜマンホールは丸いのでしょうか?丸以外の形のマンホールだとどうなるのか考えてみましょう。
直線と角
本節では直線と角の考え方を理解します。直線はふつう両方に限りなくのびているものとして考えます。2点 ${\rm A}$, ${\rm B}$ を通る直線は1つしかひけず直線 ${\rm AB}$といいます。また直線 ${\rm AB}$ のうちの2点 ${\rm A}$, ${\rm B}$ の間の部分を線分 ${\rm AB}$ といいます。これまで意識することはなかったかもしれませんが、三角形の辺や円の直径などは「線分」です(線分 ${\rm AB}$ を ${\rm B}$ の方へまっすぐ限りなく伸ばしたものを半直線 ${\rm AB}$ といいます)。三角形 ${\rm ABC}$ は記号を使って ${\rm \triangle{ABC}}$ と表します。また平行な2直線を平行線といい、2直線 ${\rm AB}$, ${\rm AB}$ が平行であることを記号を用いて ${\rm AB}/ \! \! /{\rm CD}$ とかきます。平行線は角を作りませんが、たとえば1つの点 $O$ から出る半直線 ${\rm OA}$, ${\rm OB}$ は角を作ります。この角を記号を使って $\angle {\rm AOB}$ と表して「角 ${\rm AOB}$」と読みます。また角の大きさが等しいことを等号を用いて、たとえば $\angle {\rm AOB} = \angle {\rm BOA}$ のように書きます。さらに、2直線が垂直であるとき、一方の直線を他方の直線の垂線といいます。線分 ${\rm AB}$ と直線 ${\rm \ell}$ が垂直であることを記号を使って ${\rm AB} \perp {\rm \ell}$ とかきます。そして線分を2等分する点を中点といい、中点を通り、その線分に垂直な直線を垂直二等分線といいます。これらの記号や用語を正しく理解し、線や角に関して、定義に従った正しい言葉で線の説明をできるようになりましょう。
直線:2点で定まる。

線分:両端のあるもの。

半直線:一端だけのあるもの。
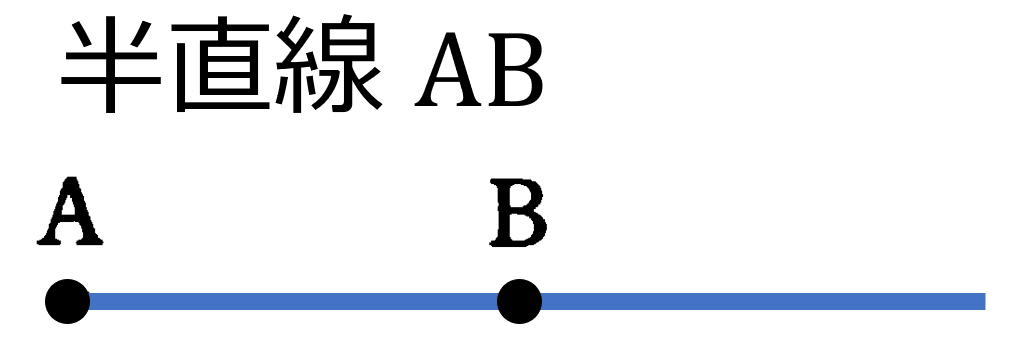
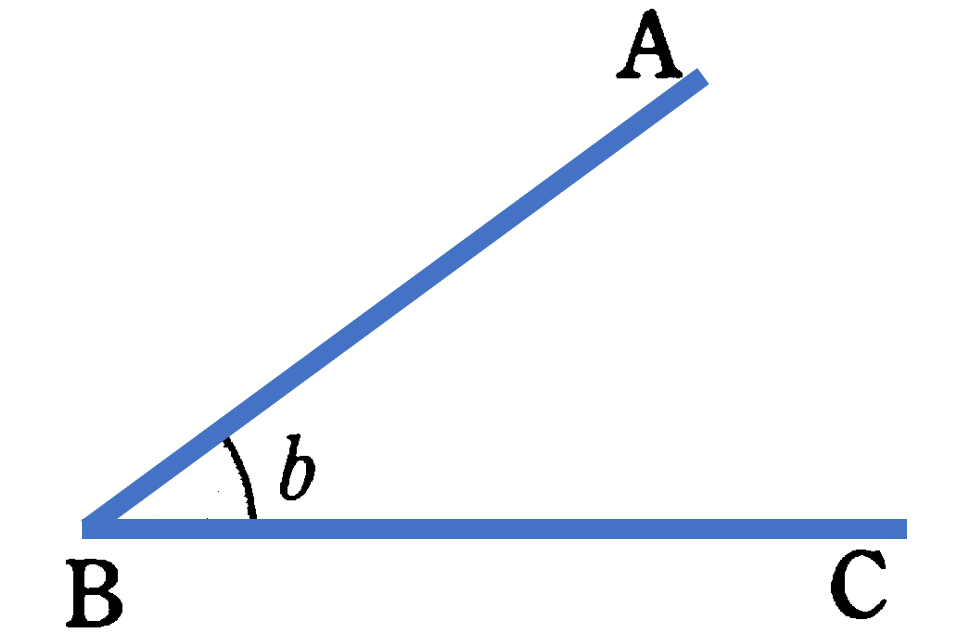
角:$\angle {\rm ABC}$の大きさを$\angle {\rm ABC}$,$\angle {\rm B}$,$\angle b$で表す。
2直線の垂直・平行:
(1) 垂直 $ \ell \perp m$:2直線 $ \ell, m $ が垂直に交わる。
(2) 平行 $ \ell / \! \! / m$:2直線 $ \ell, m $ が交わらない。
距離:「最短」の線分の長さのこと。
(1) 2点間の距離:2点を結ぶ線分の長さ。
(2) 点と直線の距離:点から直線にひいた垂線の長さ。
(3) 平行線の距離:平行な2直線の一方の上にある点と他方の直線との距離。
図形の移動
ある図形を形や大きさを変えずにほかの位置に移すことを移動といいます。本節では図形の移動を理解・利用して、様々な問題について考えてみましょう。
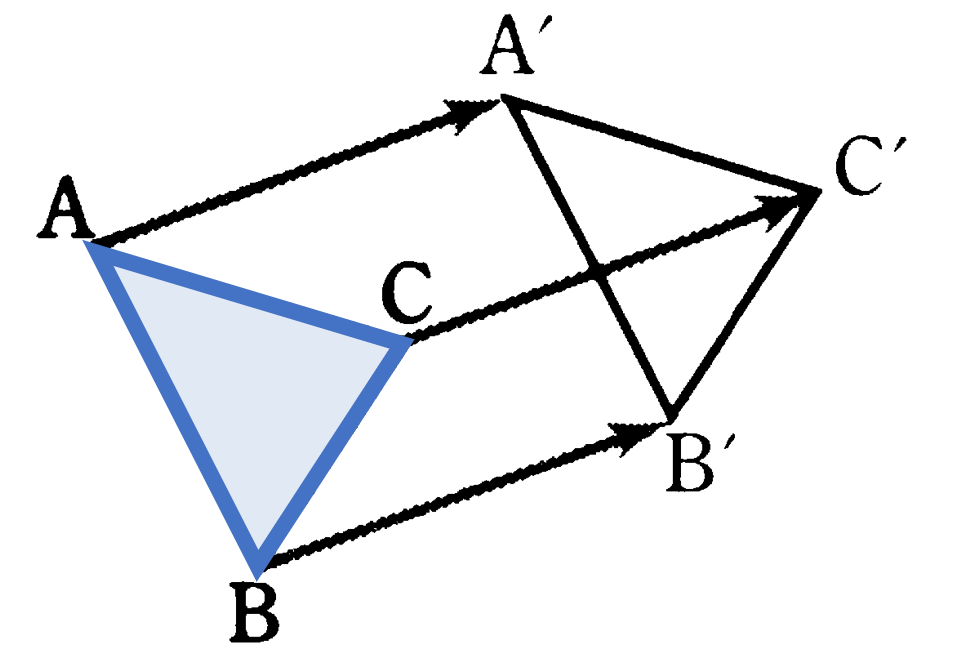
平行移動:図形を一定の方向に一定の距離だけずらす移動。
平行移動の性質:対応する点を結ぶ線分は平行で長さが等しい。
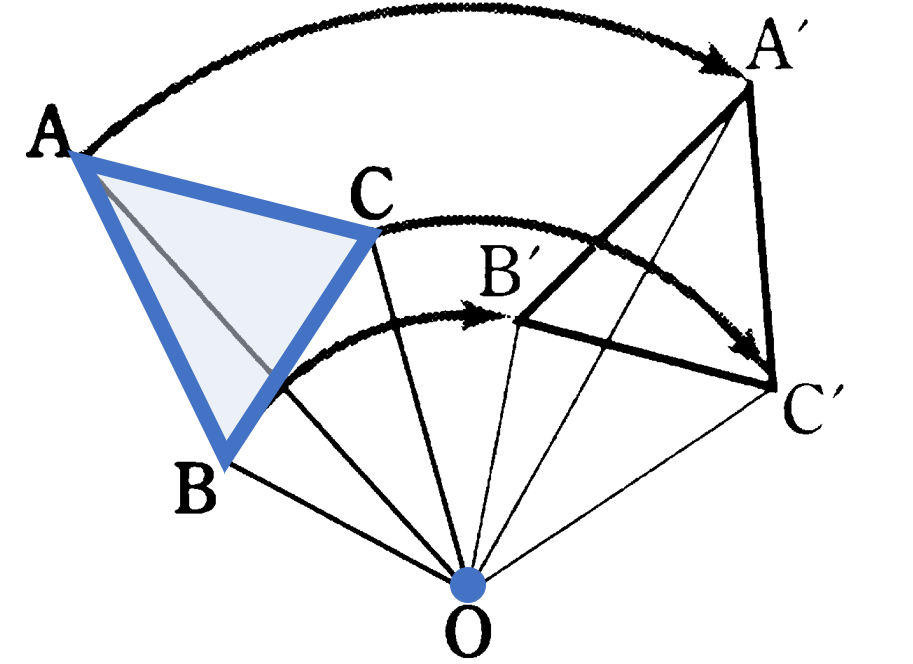
回転移動:図形をある点 $O$ を中心にして一定の角度だけ回転させる移動。中心とする点 $O$ は回転の中心という。
回転移動の性質:対応する点は回転の中心から等しい距離にあり、対応する点と回転の中心とを結んでできる角の大きさが全て等しい。
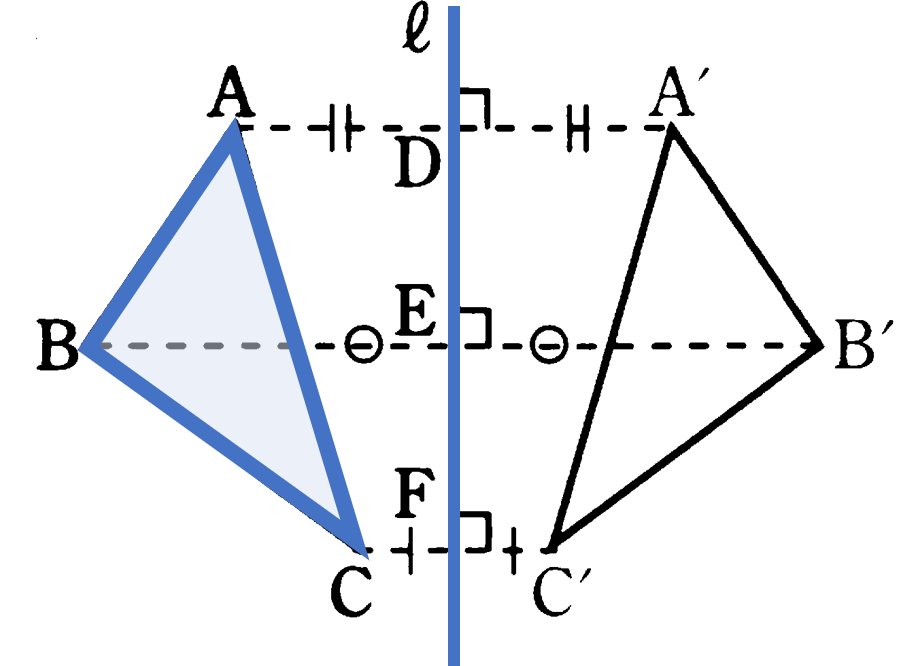
対称移動:図形を1つの直線 $\ell$ を折り目として折り返す移動。直線 $\ell$ を対称の軸という。
対称移動の性質:対称の軸は対応する2点を結ぶ線分の垂直二等分線になる。
作図
あなたの筆箱には何が入っているでしょうか。本節では定規とコンパスだけを使って、どんな図形がかけるかを考えます。これらの2つの簡単な道具を工夫して使うことで、驚くほど多様な図形を描くことができるようになります。そのためにも、作図の工程のひとつひとつの意味を正確に理解していきましょう。
作図:定規とコンパスだけを用いて図形を描くことを「作図」という。定規は直線をひくために、コンパスは円をかくために用いる。またコンパスは等しい長さをとったり、線分を移したりすることができる。また作図のためにかいた「必要な線」は消さない。
線分の垂直二等分線・中点
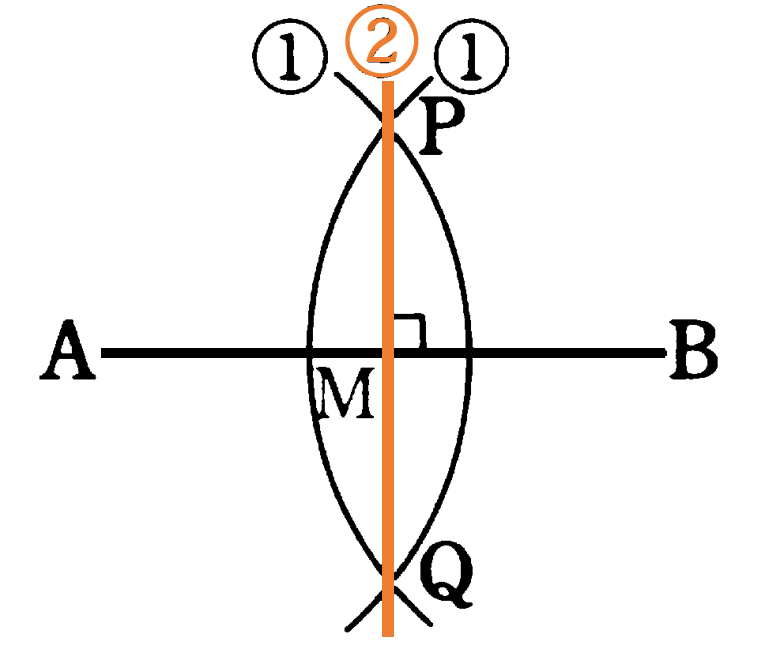
※ 線分の両端の点を中心に、等しい半径の円を2つかき、その2つの円上にできる2つの交点を結ぶことで、線分の垂直二等分線をかくことができる。垂直二等分線が、2つの点から距離が等しい点の集まりであることを理解していれば、この作図方法を理解しやすい。
角の二等分線
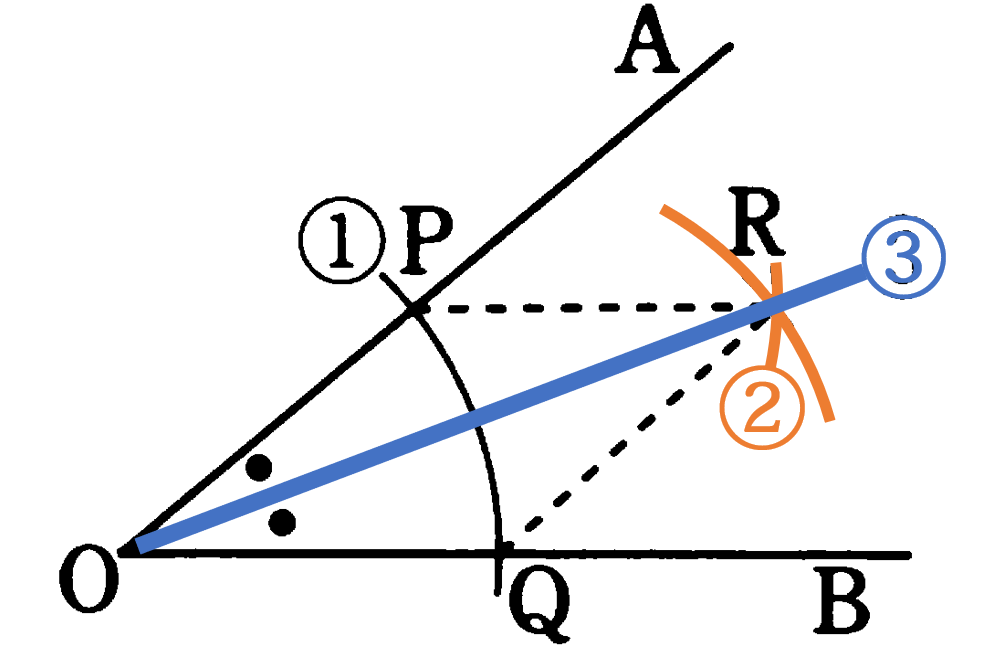
※ 1つの角を2等分する半直線を、その角の二等分線という。角の二等分線上のどの点をとっても、角の2辺までの距離が等しく点の集まりであることを理解していれば、この作図方法を理解しやすい。
直線への垂線
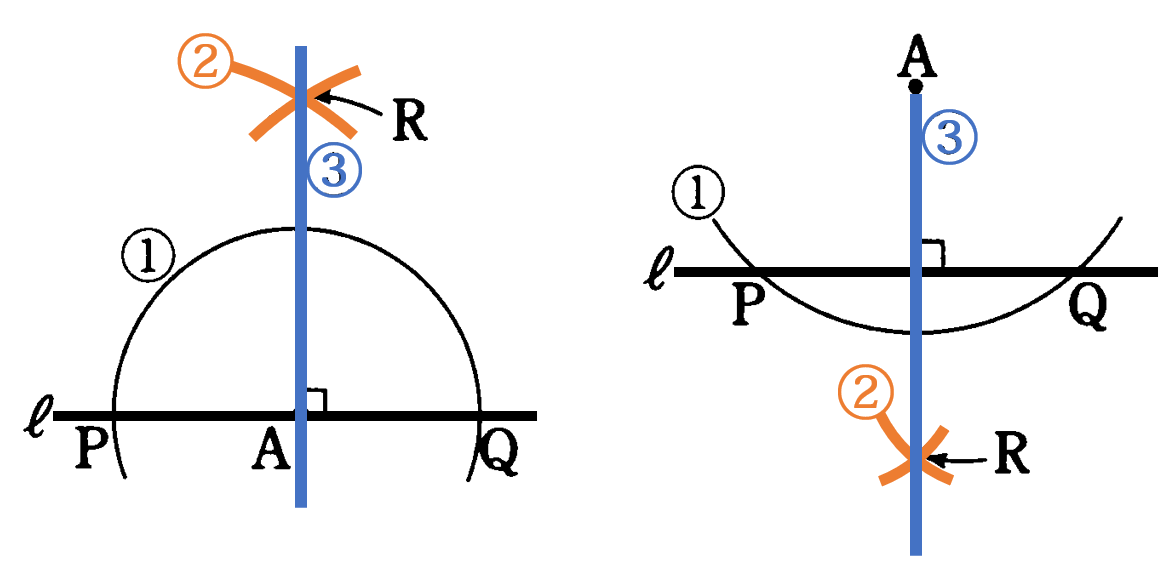
※ 直線への垂線が、直線上のある2点から等しい距離にある点の集まりであることを理解していれば、この作図方法を理解しやすい。
円と作図:
(1) 弧:円周上の2点をA,BとするときAからBまでの円周の部分を弧 ${\rm AB}$ といい $\stackrel{\frown}{AB}$ と表す。
(2) 弦:円周上の2点を結ぶ線分を弦といい、両端がA,Bである弦を弦 ${\rm AB}$ という。
(3) 接する:直線が1点だけで円と交わる場合を、直線が円に接するといい、この直線を接線、円と直線とが接する点を接点という。
(4) 円の接線:円の接線は接点を通る半径に垂直。円の接線が、接線を対称の軸として移動させた円の中心と元の円の中心の2点から等しい距離にある点の集まりであることを理解していれば作図できる。
いろいろな作図:
(1) 点を決めるには2直線や2円の交点や直線と円の交点とする。
(2) 直線を決めるには通る2点を選ぶ。
円とおうぎ形
車のワイパーがふき取る部分の形や扇子の形、日本の伝統模様の「青海波」の柄など、目にする機会が多いおうぎ形。おうぎ形は円の一部で、弧の両端の点を通る2つの半径(2つの線分)とその弧で囲まれた図形です。おうぎ形で、2つの半径のつくる角を中心角といいます。本節では、おうぎ形の弧の長さや面積などの特徴について理解しましょう。
半径 $r$ の円:周の長さ $\ell=2 \pi r$, 面積 $S=\pi r^2$
半径 $r$ 中心角 $a^\circ$ のおうぎ形:弧の長さ $\ell=2 \pi r \times \frac{a}{360}$, 面積 $S=\pi r^2 \times \frac{a}{360}=\frac{1}{2}\ell r$
※ 1つの円(半径 $r$ が決められた時)ではおうぎ形の弧の長さと面積は中心角の大きさに比例する。

