🔄 最終更新日 2020年7月13日 by takara_semi
本記事では中学3年で学習するすべての項目について、その概要を確認します。分からないところがあれば一度目はとばして読み進めてみましょう。そして、1年と2年の内容を確認したり、分からない部分を考えながら過ごす中で、突然、はっきりと理解できる日が訪れることでしょう。それでは、中学数学の完成を目指して一つずつ内容を確認していきましょう。中3 > 1章:式の計算
中学1年~2年では、多項式どうしの加法や減法を学習しましたが、本章では、多項式どうしの乗法と除法を習得し、文字を使った式やその計算を利用した様々な問題解決の方法について学んでいきましょう。
式の乗法・除法
本節では、分配法則を利用した単項式と多項式の乗法や、逆数を利用した多項式と単項式の除法、分配法則を繰り返し利用して計算する多項式と多項式の乗法の計算方法について理解しましょう。多項式と多項式の乗法 $(a+b)(c+d)$ は例えば $c+d=M$ とおけば $(a+b)M$$=aM+bM$$=a(c+d)+b(c+d)$$=ac+ad+bc+bd$ として計算することができます。このように、単項式や多項式の積の形の式を、括弧を外して単項式の和の形に直すことを、式を展開すると言います。次に、式の展開を楽にするための「乗法公式」についてみていきましょう。
【公式1】$(x+a)(x+b)$$=x^2+ax+bx+ab$$=x^2+(a+b)x+ab$
つまり $x^2+(aとbの和)x+(aとbの積)$ という形になります。続いて公式1の $b$ を $a$ におきかえると
【公式2】$(x+a)^2$$=x^2+2ax+a^2$
公式2の $a$ を $-a$ におきかえると
【公式3】$(x-a)^2$$=x^2-2ax+a^2$
公式1の $b$ を $-a$ におきかえると
【公式4】$(x+a)(x-a)$$=x^2-a^2$
このように公式1を導くことによって公式2~4をつくることができます。
\begin{eqnarray}
(3x+1)(3x-2) &=& (X+1)(X-2) \\
&=& X^2-X-2 \\
&=& (3x)^2-(3x)-2 \\
&=& 9x^2-3x-2
\end{eqnarray}
と展開できます。他にも $(x+y-1)(x+y+1)$ という式の展開は $x+y=A$ として1つの文字として扱うことで【公式4】より
\begin{eqnarray}
(x+y-1)(x+y+1) &=& (A-1)(A+1) \\
&=&A^2-1 \\
&=&(x+y)^2-1 \\
=&x^2&+2xy+y^2-1
\end{eqnarray}
と展開できます。このように、文字を置き換えて考えることで、乗法公式を利用して簡単に展開できる計算が多くあります。乗法公式を確実に理解して、式の展開を正確にできるように練習しましょう。
(1) (単項式) $\times$ (多項式):分配法則を用いて多項式の各項に単項式をかける。
例
$a(b―c+d)=ab-ac+ad$
(2) (多項式) $\div$ (単項式):乗法の形になおして計算する。
例
$(15a^2b^2-10ab^3) \div 5ab^2$ $=(15a^2b^2-10ab^3) \times \frac{1}{5ab^2}$ $=\frac{15a^2b^2-10ab^3}{5ab^2}$ $=3a-2b$
(3) (多項式) $\times$ (多項式):分配法則をくり返し用い計算する。
例
$(a+b)(c+d)$$=a(c+d)+b(c+d)$$=ac+ad+bc+bd$
展開の公式:
(1) $x^2+(和)x+(積)$ の形:$(x+a)(x+b)$$=x^2+(a+b)x+ab$
(2) $(x+a)^2$ の形:$(x+a)^2=x^2+2ax+a^2$
(3) $(x-a)^2$ の形:$(x-a)^2=x^2-2ax+a^2$
(4) $(和) \times (差)$ なら平方の差:$(x+a)(x-a)=x^2-a^2$
因数分解
本節では、因数分解の考え方について理解しましょう。まずは、多項式をいくつかの式の積で表現することを考えます。例えば多項式 $x^2+4x+3$ は $x^2+4x+3$$=(x+3)(x+1)$ という等式が成り立ちます。多項式 $x^2+4x+3$ を $(x+3),(x+1)$ に分解できたと考えることができます。このとき $(x+3),(x+1)$ を $x^2+4x+3$ の因数といいます。$3xy$ では $3,x,y,xy$ などが因数、数 $6$ では $6=2 \times 3$ と表せるため $2,3$ は $6$ の因数となります。このように、多項式をいくつかの因数の積としてあらわすことを、その多項式を因数分解するといいます。また $ma+mb+mc$ のように多項式の各項に共通な因数がある場合、それを括弧の外にくくりだすことで $m(a+b+c)$ というようにして式を因数分解することができます。また式を因数分解するとき、可能な限り因数分解したものを解答とします(多項式 $4abx+6aby$ は $a(4bx+6by)$ としても因数分解したことになりますが、式の中井に共通の因数 $2,b$ が残っているため、因数分解としては不正解です。可能な限り因数分解すると答えは $2ab(ax+3y)$ となります)。
続いて、式を展開する時に利用した「乗法公式」を逆に使うことで因数分解する方法を考えてみましょう。これまでに学んだ乗法公式の逆をまとめると (1) $x^2+(a+b)x+ab$$=(x+a)(x+b)$ (2) $x^2+2ax+a^2=(x+a)^2$ (3) $x^2-2ax+a^2=(x-a)^2$ (4) $x^2-a^2=(x+a)(x―a)$ となります。これらの関係を利用することで、式を簡単に因数分解することができるようになります。他にも、式の展開のときと同じように、文字の置き換えなどを利用することで、乗法公式の逆を使って因数分解できる場合も多くあります。たくさんの問題に取り組み、因数分解の手順に慣れていきましょう。
次の手順で因数分解する:
(1) 共通因数でくくる。
例1)$ma+mb=m(a+b)$
例2)$ma+mb-mc$$=m(a+b-c)$
(2) 因数分解の公式を用いる。$\to$ 展開の公式(1)~(4)と同じ。
例1)$x^2+(a+b)x+ab$$=(x+a)(x+b)$
例2)$x^2+2ax+a^2=(x+a)^2$
例3)$x^2-2ax+a^2=(x-a)^2$
例4)$x^2-a^2=(x+a)(x―a)$
式の計算の利用
ここまでに学んだ「展開」や「因数分解」を利用して、いろいろな問題を考えてみましょう。例えば $101^2-99^2$ という計算は因数分解を利用すると $(101+99)(101-99)$$=200 \times 2$$=400$ というように、簡単に計算することができます。演習を繰り返して、問題に応じてどのような公式を利用すれば上手く工夫して計算できるかを判断できるようになりましょう。
整数の問題への利用:(以下$n$は自然数)
(1) 偶数は例えば $2n$ 奇数は例えば $2n-1$ と表現できる。
(2) 連続する3つの自然数は例えば $n,n+1,n+2$ と表現できる。
素因数分解
本節では、素因数分解の方法について理解しましょう。素因数分解の知識は、次節で学ぶ平方根の計算にも利用できます。また実生活のなかでは、暗号化技術などにも応用されている奥が深い単元です。興味のある方は、暗号解読に関する書籍などを読んでみて下さい。きっと夢中になるはずです。
因数:自然数がいくつかの自然数の積で表されるとき、その一つ一つの数をもとの数の因数という。例えば $196$ は $196=4 \times 49$ と表せるため $4$ や $49$ は $196$ の因数である。
素数:$1$ とその数の他に約数がない数。つまり、それより小さい自然数の積で表すことができない自然数。例えば $2=2 \times 1$,$3=3 \times 1$,$5=5 \times 1…$ など。ただし $1$ は素数ではない。
素因数:素数である因数。例えば $196$ は $196=2^2 \times 7^2$ と表せるため $2$ と $7$ が $196$ の素因数である。
素因数分解:自然数を素因数だけの積として表すこと。
例
$360$を素因数分解すると $360=2^3 \times 3^2 \times 5$
中3 > 2章:平方根
本章では、$2$ 乗して $a$ になる数やその計算について学びましょう。過去には「禁じられた悪魔の数」とされた歴史もある平方根の利便性と奥深さを垣間見れることでしょう。
平方根
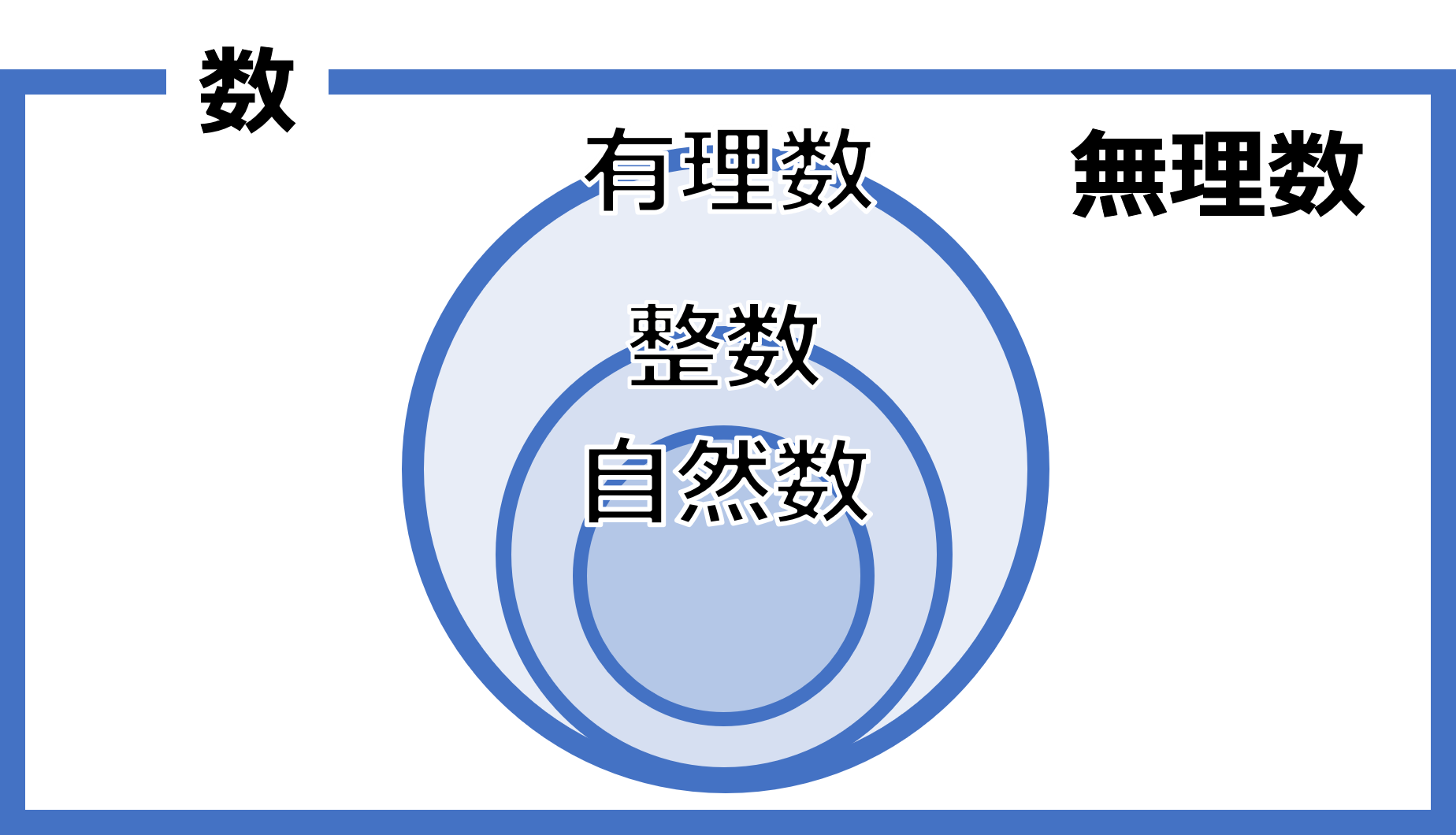
本節では平方根の考え方をみていきます。まず、$2$ 乗して $5$ になる数とはどのような数でしょうか。つまり $x^2=5$ となるような $x$ の値です。この $x$ を小数で表現すると $2.2360679…$ となり、限りなく続く小数になります(このような、現れる数にパターンがなく、無限に続く小数を無理数といいます。また $a$ を整数 $b$ を $0$ でない整数としたとき $\frac{a}{b}$ で表現できる数は有理数といいます。つまり $3=\frac{3}{1}, 0.1=\frac{1}{10}, \sqrt{9}=3$ などは有理数で $\sqrt{2}, \sqrt{3}, \pi$ などは無理数であるといえます)。この数を根号とよばれる記号 $\sqrt{ }$ を用いて $\sqrt{5}$ と表し「ルート $5$」と読みます(「root,radix:根」の頭文字「r」が起源との説があります)。一般に、ある数 $x$ を $2$ 乗すると $a$ になるとき $x$ を $a$ の平方根といいます。例えば $2,-2$ は $2$ 乗すると $4$ になるため $2,-2$ は $4$ の平方根だといえます。このように、正の数には平方根が2つのあり、絶対値が等しく符号が異なります( $4$ の平方根は $\sqrt{4}=2,-\sqrt{4}=-2$ の2つ)。また $0$ の平方根は $0$ のみ( $\sqrt{0}=0$ )であり、負の数の平方根は考えません(厳密には高校数学で虚数という概念を学習すれば扱うことができます)。 また平方根の大小関係は $a,b$ が正の数で $a < b$ ならば $\sqrt{a} < \sqrt{b}$ という関係が成り立ちます。例えば $0.1$ と $0.01$ の平方根の大小は $\sqrt{0.01} < \sqrt{0.1}$($0.1 < \sqrt{0.1}$) となります。平方根の基本的な性質や概念を理解し、数の世界の広がりを感じましょう。
※ 平方根とは2乗してもとの数になるものをいいます。なので2乗して $9$ になる数は $3$ と $-3$ の2つが考えられ $9$ の平方根は $±\sqrt{9}=±3$ と表現をします。一方で、ルート $\sqrt{ }$ という記号は正の数を表すものなので $\sqrt{9}=3$ となります。負の数を表現するときは $-\sqrt{9}=-3$ となります。平方根を答えなさい、という場合と、計算の記号としての根号とを、きちんと区別して正しく答えられるように理解しましょう。
(1) $a$の平方根 $\to$ 2乗(平方)すると$a$になる数。$x^2=a$ を満たす $x$ の値のこと。
(2) 正の数の平方根 $\to$ 正・負の2つ。
(3) 0の平方根 $\to$ 0
(4) 負の数の平方根 $\to$ ない。(※ 厳密には高校数学で虚数というものを学習する)
(5) $a > 0$ のとき $a$ の平方根 $\to$ 正の方を $\sqrt{a}$ 負の方を $-\sqrt{a}$と表す。
(6) $a > 0$ のとき $(\sqrt{a})^2=a$, $(-\sqrt{a})^2=a$, $\sqrt{a^2}=a$, $\sqrt{(-a)^2}=a$
(7) $a > 0$, $b > 0$ のとき $a < b \iff \sqrt{a} < \sqrt{b}$
$\sqrt{2}≒1.41421356$ $\to$ 一夜一夜に 人見ごろ
$\sqrt{3}≒1.7320508$ $\to$ 人なみに おごれや
$\sqrt{5}≒2.2360679$ $\to$ 富士山ろく オウム鳴く
$\sqrt{6}≒2.44949$ $\to$ 似よ よくよく
$\sqrt{7}≒2.64575$ $\to$ (菜) に虫いない
数学が面白くなる動画―15
禁じられた数字。平方根は悪魔の数?
有理数と無理数:
(1) 有理数 $\to$ 分数の形で表現できる数。
例
$\frac{1}{3}, 0.13$($=\frac{13}{100}$ と表現できる)
(2) 無理数 $\to$ 分数の形で表現できない数。循環しない無限小数。
例
$\sqrt{2}, \pi$
数学が面白くなる動画―16
平方根が決して分数で表現できない無理数であるということを証明できますか?
根号を含む式の計算
本節では、根号を含む計算の方法について考えてみましょう。平方根の積と商は $a,b$ を正の数とするとき (1) $\sqrt{a} \times \sqrt{b}$$=\sqrt{a} \sqrt{b}$$= \sqrt{ab}$ (2) $\sqrt{a} \div \sqrt{b}$$= \frac{\sqrt{a}}{\sqrt{b}}$$= \sqrt{\frac{a}{b}}$ と計算できます。計算の結果、根号を使わずに表すことができる部分は、根号を使わずに表します($\frac{\sqrt{198}}{\sqrt{11}}$$=\sqrt\frac{198}{11}$$=\sqrt{18}$$=\sqrt{2 \times 3^2}$$=3\sqrt{2}$)。根号の中の数を素因数分解することで、根号の外に出す数を見つけやすくなります。
続いて、分数の計算をやりやすくするため「分母に根号がある数の分母を整数に直す方法」について考えてみましょう。分母に根号がある数は、分母分子に同じ数をかけることで、分母に根号がない形に直すことができます。例えば $\frac{\sqrt{5}}{2\sqrt{3}}$$=\frac{\sqrt{5} \times \sqrt{3}}{2\sqrt{3} \times \sqrt{3}}$$=\frac{\sqrt{15}}{2 \times 3}$$=\frac{\sqrt{15}}{6}$ のように計算します。このように、分母に根号がない形に直すことを分母を有理化するといいます。少し複雑な有理化の例としては $\frac{c}{\sqrt{a} + \sqrt{b}}$ のような式を有理化する方法を考えると、この場合、分母分子に $\sqrt{a} – \sqrt{b}$ をかけることで、乗法公式で学習した $(a+b)(a-b)$$=a^2-b^2$ の形を分母に作ることができ、根号をなくすことができます。先の例では $\frac{c}{\sqrt{a} + \sqrt{b}}$$=\frac{c(\sqrt{a} – \sqrt{b})}{(\sqrt{a} + \sqrt{b})(\sqrt{a} – \sqrt{b})}$$=\frac{c(\sqrt{a} – \sqrt{b})}{a-b}$ となり、分母を有理化することができます。
最後に、根号を含む式の加減についてみていきましょう。例えば $\sqrt{5}+\sqrt{3}$ という式はこれ以上簡単にすることはできません(この式自体が1つの数を表しています)。一方で、例えば $7\sqrt{5}+2\sqrt{5}$ という式は、同じ数の平方根を含んだ式を同類項としてまとめて簡単にすることができます。先の例では $7\sqrt{5}+2\sqrt{5}$$=(7+2)\sqrt{5}$$=9\sqrt{5}$ となります。平方根を含む数の計算は、演習を繰り返して慣れておけば、決して困難なものではありません。ひとつずつ知識を整理し、着実に身に付けていきましょう。
※ 根号を含むの計算問題では、計算結果に (1) 根号の中の数に2乗の因数はないか(根号の外に出せる数はないか) (2) 分母に根号がないか(有理化できているか)を必ず確認しましょう。
平方根の乗法・除法:以下 $a > 0$, $b > 0$, $k > 0$ とする。
例1
$\sqrt{a} \times \sqrt{b}=\sqrt{ab}$
例2
$\sqrt{k^2a}=k\sqrt{a}$
例3
$\frac{\sqrt{b}}{\sqrt{a}}=\sqrt{\frac{b}{a}}$
例4
$\sqrt{\frac{a}{k^2}}=\frac{\sqrt{a}}{k}$
例1
$\ell \sqrt{a} + m \sqrt{a}=(\ell + m)\sqrt{a}$
例2
$\frac{1}{\sqrt{a}}=\frac{\sqrt{a}}{a}$ (分母分子に $\sqrt{a}$ を掛ける)
例
$a=\sqrt{3}+\sqrt{5}$, $b=\sqrt{3}-\sqrt{5}$ のとき $a^2-b^2$ の値を求める。この場合そのまま式に値を代入するのではなく先に式を変形する。
\begin{eqnarray}
a^2-b^2 &=& (a+b)(a-b) \\
&=& 2 \sqrt{3} \times 2 \sqrt{5} \\
&=& 4 \sqrt{15}
\end{eqnarray}
となる。
中3 > 3章:2次方程式
中学1年では1次方程式の解き方を学びました。本章では、そこから少し発展させ、次数が「2」である2次方程式について、その解き方や利用方法について考え、方程式によって解決できる問題の幅を広げていきましょう。
2次方程式
本節では、2次方程式の解法について学びます。2次方程式とは、移項によって $ax^2+bx+c=0 (a \neq 0)$ つまり(2次式)$=0$ の形に変形できる方程式のことをいいます。2次方程式を成り立たせる文字の値を、その方程式の解といい、2次方程式の解を全て求めることを、2次方程式を解くといいます。2次方程式の解法は大きく (1) 因数分解を利用した解法 (2) 平方根の考え方を利用した解法 (3) 解の公式を利用した解法 があります。どの方法で解いても解は同じになるので、式の形によって、どの方法で解くのが良さそうかを判断しましょう。以下、それぞれの解法についてみていきます。
因数分解を利用いた解法:2次方程式の左辺が因数分解してあって、右辺が $0$ のときには、左辺の因数の一方を $0$ にする $x$ の値は解になります。つまり、2次方程式 $ax^2+bx+c=0$ の左辺が因数分解できるときには「$AB=0$ ならば $A=0$ または $B=0$」ということを利用して2次方程式を解くことができます。例えば $(x-2)(x-3)=0$ を解くと、$(x-2)=0$,$(x-3)=0$ となる $x$ が解であるから、方程式の解は $x=2,3$ となります。
平方根の考え方を利用した解法:$ax^2+c=0$ の形をした2次方程式は、平方根の考えを使って解くことができます。例えば $x^2-9=0$ という方程式は $x^2=9$ と変形でき $x$ が $9$ の平方根であることを示しており $x=±3$ と解くことができます。ここで $x=±3$ は $x=3,-3$ をまとめて示しています。次に $(x+a)^2=c$ の形をした2次方程式は、括弧の中をひとまとまりのものとみることで、平方根の考えを利用して解くことができます。例えば $(x-2)^2-3=0$ という方程式は $(x-2)^2=3$ と変形でき $x-2$ が $3$ の平方根であることを示しており $x-2=±\sqrt{3}$ となり $x=2±\sqrt{3}$ として解くことができます。最後に $x^2+px+q=0$ の形をした2次方程式についても、平方根の考えを使って解くことができます。この解法については、次の内容で説明する「2次方程式の解の公式」の導出過程と同じ計算によって解くことができるので、そちらを参考に理解を深めましょう。
解の公式を利用した解法:2次方程式 $ax^2+bx+c=0$ の解が解の公式 $x=\frac{-b± \sqrt{b^2-4ac}}{2a}$ となることを証明します。
\begin{eqnarray}
ax^2+bx+c &=& 0 \\
x^2+\frac{b}{a}x+\frac{c}{a} &=& 0 \\
x^2+\frac{b}{a}x &=& -\frac{c}{a} \\
x^2+\frac{b}{a}x+\left( \frac{b}{2a} \right)^2 &=& -\frac{c}{a}+\left( \frac{b}{2a} \right)^2 \\
\left( x+\frac{b}{2a} \right)^2 &=& -\frac{4ac-b^2}{4a^2} \\
x+\frac{b}{2a} &=& ±\sqrt{\frac{b^2-4ac}{4a^2}} \\
x &=& -\frac{b}{2a}±\frac{\sqrt{b^2-4ac}}{2a} \\
x &=& \frac{-b±\sqrt{b^2-4ac}}{2a}
\end{eqnarray}
上記の計算の結果、解の公式が導かれます。
ポイントは、一般に $x^2+px$ という式を $(x+A)^2$ のような平方の形にするには $x$ の係数 $p$ の $\frac{1}{2}$ の2乗である $\left( \frac{p}{2} \right)^2$ を加えればよいという点です。つまり $x^2+px+\left( \frac{p}{2} \right)^2$$=\left( x+\frac{p}{2} \right)^2$ となることを理解した上で計算しましょう。
2次方程式を解くときに毎回この計算をするのは効率的でないため、解の公式は暗記してしまうのが間違いなく便利です。例えば $2x^2-2x-1=0$ を解の公式を使って解くと、解の公式に $a=2,b=-2,c=-1$ を代入すると
\begin{eqnarray}
x &=& \frac{-(-2)±\sqrt{(-2)^2-4\times 2 \times (-1)}}{2 \times 2} \\
x &=& \frac{2±\sqrt{4+8}}{4} \\
x &=& \frac{2±\sqrt{12}}{4} \\
x &=& \frac{2±2\sqrt{3}}{4} \\
x &=& \frac{1±1\sqrt{3}}{2}
\end{eqnarray}
したがって $x = \frac{1±1\sqrt{3}}{2}$ と解くことができます。
2次方程式の解法①:
(1) 因数分解を利用して解く。
例
($x-a)(x-b)=0$ の解 $\to$ $x=a,b$
2次方程式の解法②:
(1) $x^2=k (k≧0)$ の解 $\to$ $x=± \sqrt{k}$
(2) $(x+m)^2=k(k≧0)$ の解 $\to$ $x=―m± \sqrt{k}$
$ax^2+bx+c=0$ の解 $\to$ $x=\frac{-b± \sqrt{b^2-4ac}}{2a}$
解の係数の関係:
$ax^2+bx+c=0$ の解を $\alpha, \beta$ とすると $\alpha+\beta=-\frac{b}{a}$, $\alpha \beta=\frac{c}{a}$ が成り立つ。この結果は解の公式から計算できる。
2次方程式の利用
この節では2次方程式を利用して問題を解決する方法について考えます。2次方程式を利用した問題解決の手順としては (1) どの数量を文字を使って表すかを決める。 $\to$ (2) 数量の間の関係をみつけて方程式をつくる。 $\to$ (3) 2次方程式を解く。 $\to$ (4) 得られた解が問題に適しているかを確かめる。というステップを踏むことで問題を解決することができます。2次方程式の本代解決への利用範囲は非常に広いので、様々な問題に触れ、どのように利用すればいいのかを十分に練習しましょう。
※ 2次方程式の解の個数:2次方程式には解が2つのものと1つ(重解:$(x-2)^2=0$ のような場合)のものと実数の解を持たないもの($x^2+1=0$ のような場合)があります。その解の個数について、2次方程式の解の公式から考えることができます。2次方程式 $ax^2+bx+c=0$ の解は $\to$ $x=\frac{-b± \sqrt{b^2-4ac}}{2a}$ であるため、この式の根号の中の値によって、解の個数が分かります。$b^2-4ac > 0$ のときには解は2つ、$b^2-4ac = 0$ のときには解は1つ、$b^2-4ac < 0$ のときには実数解は0ことなります。この $b^2-4ac$ は判別式とも呼ばれます。
変数 $x$ を使って式をつくる:
(1) 等しい2つの量を見つける。
例
連続する2つの正の奇数の積が$35$となる2つの整数を求める。2つの奇数は $2x-1$, $2x+1$ と表現できる。これと$35$が等しいのだから
\begin{eqnarray}
(2x-1)(2x+1) &=& 35 \\
4x^2-1 &=& 35 \\
4x^2 &=& 36 \\
x^2 &=& 9 \\
x &=& ±3 \\
\end{eqnarray}
となる。求めるのは正の整数なので問題に合う解は $x=3$ となり $5,7$ が答えとなる。
(2) 1つの数量を2通りに表す。
これらの等しい数量を2通りで表現することで求めたい数(解)を計算することができる。
中3 > 4章:関数 $y=ax^2$
1年・2年においても、問題を解決するために関数の関係にある2つの数量を扱う方法を学びました。本章では、比例・反比例・1次関数では扱うことができない2つの数量の関係について、新しい関数 $y=ax^2$ の関係を利用する方法について学びましょう。
関数 $y=ax^2$ とそのグラフ
本節では、坂道を転がるボールのように、もしくは木から落ちたリンゴのように、時間にともなって進む距離がだんだんと増えていくような変化の様子を表現する方法について考えてみましょう。$y$ が $x$ の関数で $y=ax^2$ と表されるとき $y$ は $x$ の2乗に比例するといいます。また $y$ が $x$ の関数で2次式 $y=ax^2+bx+c$ で表されるとき $y$ は $x$ の2次関数であるといいます。$y=ax^2$ は2次関数の特別な場合であるといえます(つまり $y$ は $x$ の2乗に比例し~という問題文があった場合は $y=ax^2$ の式を考えればよいということです)。
続いて関数 $y=ax^2$ のグラフについてみていきましょう。$y=ax^2$ のグラフの特徴には (1) 原点を通る。(2) $y$ 軸について対称な曲線である。(3) $a > 0$ のときは上に開いた形 $a < 0$ のときは下に開いた形になる。(4) $a$ の値の絶対値が大きいほどグラフの開きは小さい(より尖った形になる)。というようなものがあります。$y=ax^2$ のグラフは放物線といい、放物線は対称の軸をもち、対象の軸と放物線との交点を、放物線の頂点といいます。関数 $y=ax^2$ において $a > 0$ のとき $x$ の値が増加すると (1) $x < 0$ の範囲では $y$ の値は減少する。(2) $x > 0$ の範囲では $y$ の値は増加する。(3) $x = 0$ では $y$ は最小値 $0$ となります。$a < 0$ の場合は $y$ の増減が反転します(おおよそのグラフを描いて確認しましょう)。$y$ の変域を求める問題では、端点の値だけでなく、放物線の頂点($x=0,y=0$)の存在に常に注意をして解きましょう。 また関数 $y=ax^2$ では $x$ がどの値からどの値まで変化するかによって変化の割合は異なり、一定ではありません(変化の割合$=\frac{yの増加量}{xの増加量}$)。放物線の問題は受験問題でもしばしばみかけますので、グラフの特徴や利用方法などを正しく理解しておきましょう。
関数 $y=ax^2$:
(1) $y$ は $x$ の2乗に比例する。
(2) $x$ の値が$2$倍,$ 3$倍, … ,$p$ 倍になる $\to$ $y$ の値は $2^2$ 倍, $3^2$ 倍, … ,$p^2$ 倍 になる。
(1) 原点を通る。
(2) $y$ 軸について対称になる。
(3) 放物線である。
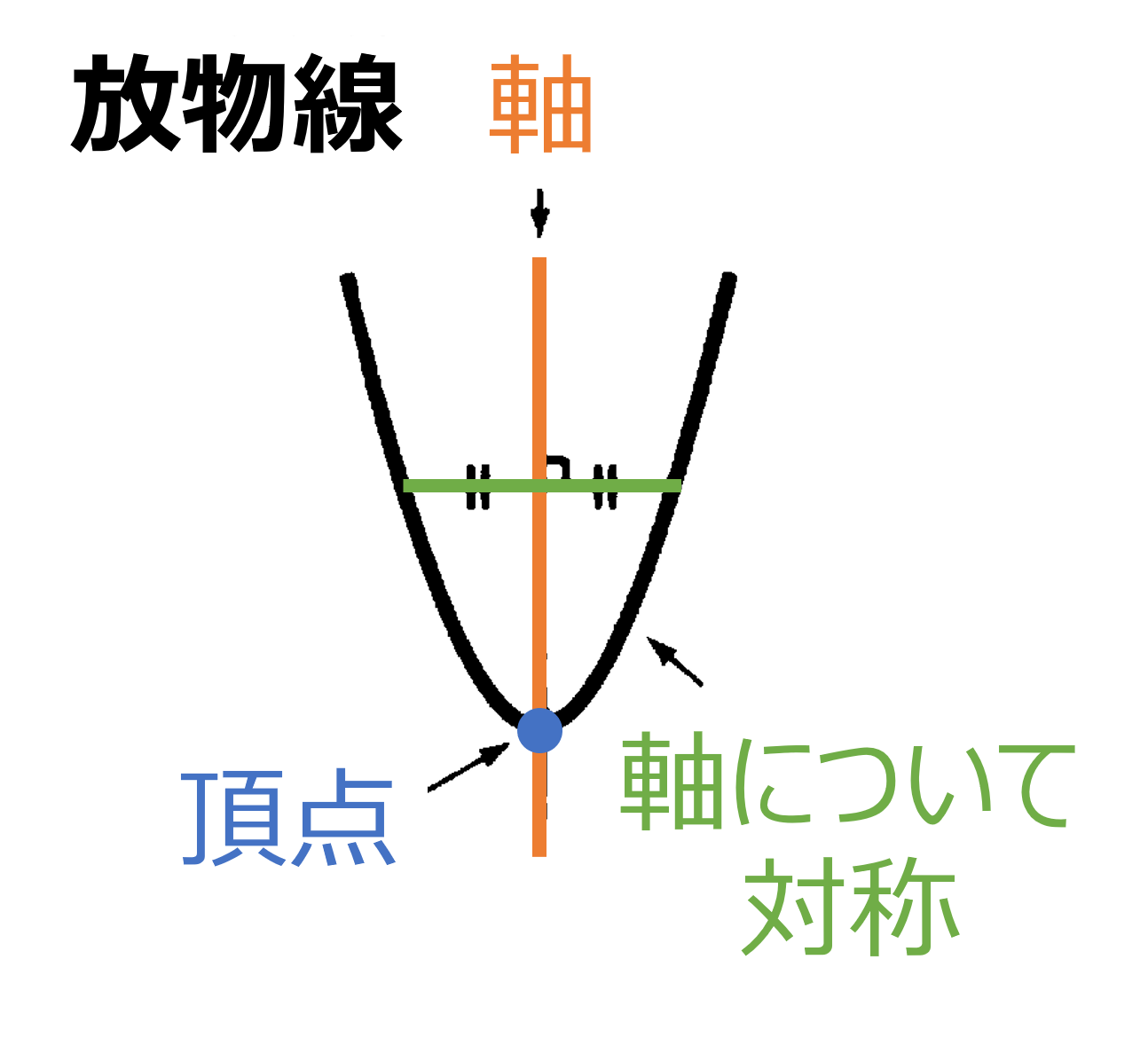
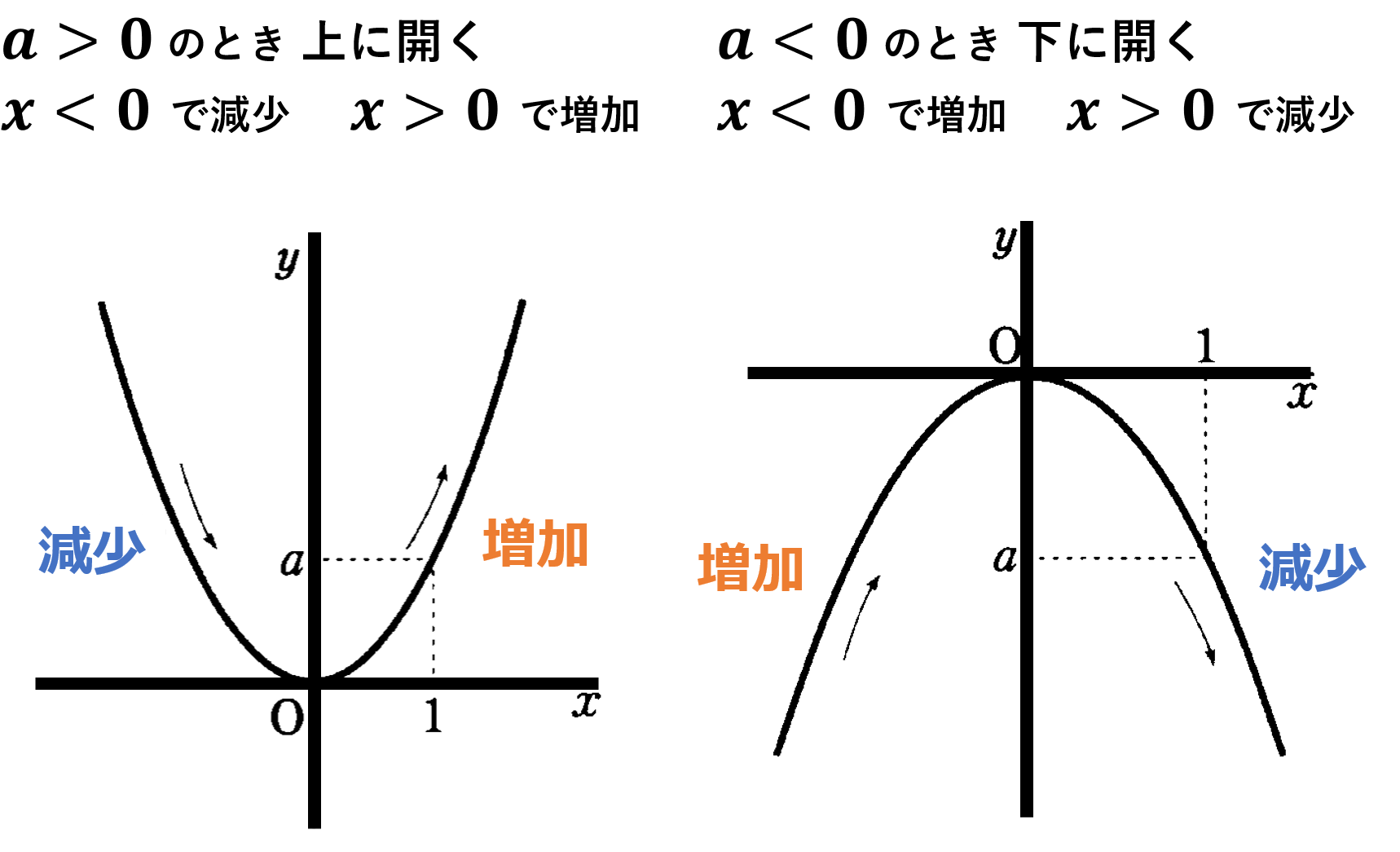
変域を求めるにはグラフを利用して考える。「端の点」と「頂点」に注目すれば分かる。
関数 $y=ax^2$ の利用
本節では、身の回りの問題を関数 $y=ax^2$ とそのグラフを利用して解決する方法について考えてみましょう。例えば、関数 $y=ax^2$ を利用することで「加速する電車が一定速度で走る車に追いつくまでの時間」を計算したりすることができます。他にも数多くのことがらを、関数 $y=ax^2$ を利用することで解決することができます。演習を繰り返して着実に実力を付けていきましょう。
放物線と直線の交点:放物線 $y=ax^2$ と直線 $y=mx+n$ の交点:
STEP1:$y$ を消去し2次方程式 $ax^2=mx+n$ を導く。
STEP2:その方程式を解き $x$ の値を求める。そして得られて $x$ を与式に代入して $y$ の値を求める。
STEP3:$(x,y)$ の組にして交点の座標とする。
いろいろな関数
本節では、身の回りにある色々な関数について考えてみましょう。例えば電車の乗車距離 $x$ と運賃 $y$ の関係は、グラフに表すと $y$ が飛び飛びの値をとる関数になります。このように、身の回り様々な数量の関係をみいだし、その関数を利用して問題を解決してみましょう。
いろいろな関数の中にはそのグラフがつながっていないものもある。
例1)電車に乗る距離 $x$ kmと運賃 $y$ 円の関係。
例2)駐車時間 $x$ 分と駐車料金 $y$ 円の関係。
実際にグラフを描いてみると不連続(階段状)であることが分かる。
中3 > 5章:相似
本章では、形が同じ図形の性質・相似の性質について学び、身の回りでその性質を利用している例をみつけてみましょう。例えば、キッチンにあるスパゲッティメジャーでは面積比の相似比の関係を利用して1人分や2人分を計測しており、調理用スプーンでは体積比と相似比の関係を利用して分量を計量できるように設計されています。このような例の他にも、直接測ることが難しい「地形や建造物の計測・縮図の作成」などにも相似が利用されています。本章の知識を身に付け、相似の性質をより身近なものとして活用できるようになりましょう。
相似な図形
本節では、形を変えずに拡大縮小して得られる図形の性質についてみていきましょう。1つの図形を、形を変えずに一定の割合に拡大縮小して得られる図形は、もとの図形と相似であるといいます。下の図で、四角形(ア)と四角形(イ)は相似です。また四角形(ウ)は四角形(イ)を左右反転した図形であり、2年で学んだ通り、この2つの四角形は合同です。このような場合にも、四角形(ア)と四角形(ウ)は相似であるといいます。四角形 $ {\rm ABCD}$ と四角形 ${\rm A’B’C’D’}$ が相似であることを四角形 $ {\rm ABCD}∽{\rm A’B’C’D’}$ と表します。多角形の相似を記号 $∽$ を用いて表す場合、合同の時と同じように、対応する頂点を周に沿って同じ順に書きます。相似な図形では、対応する部分の長さの比は全て等しく、対応する角の大きさはそれぞれ等しくなります。また、下の図の四角形(ア)と四角形(イ)のように、2つの図形の対応する点どうしを通る直線が全て1つの点 ${\rm O}$ に集まり、点 ${\rm O}$ から対応する点までの距離の比が全て等しいとき、それらの図形は、点 ${\rm O}$ を相似の中心として相似の位置にあるといいます。つまり相似の位置にある2つの図形は相似です。
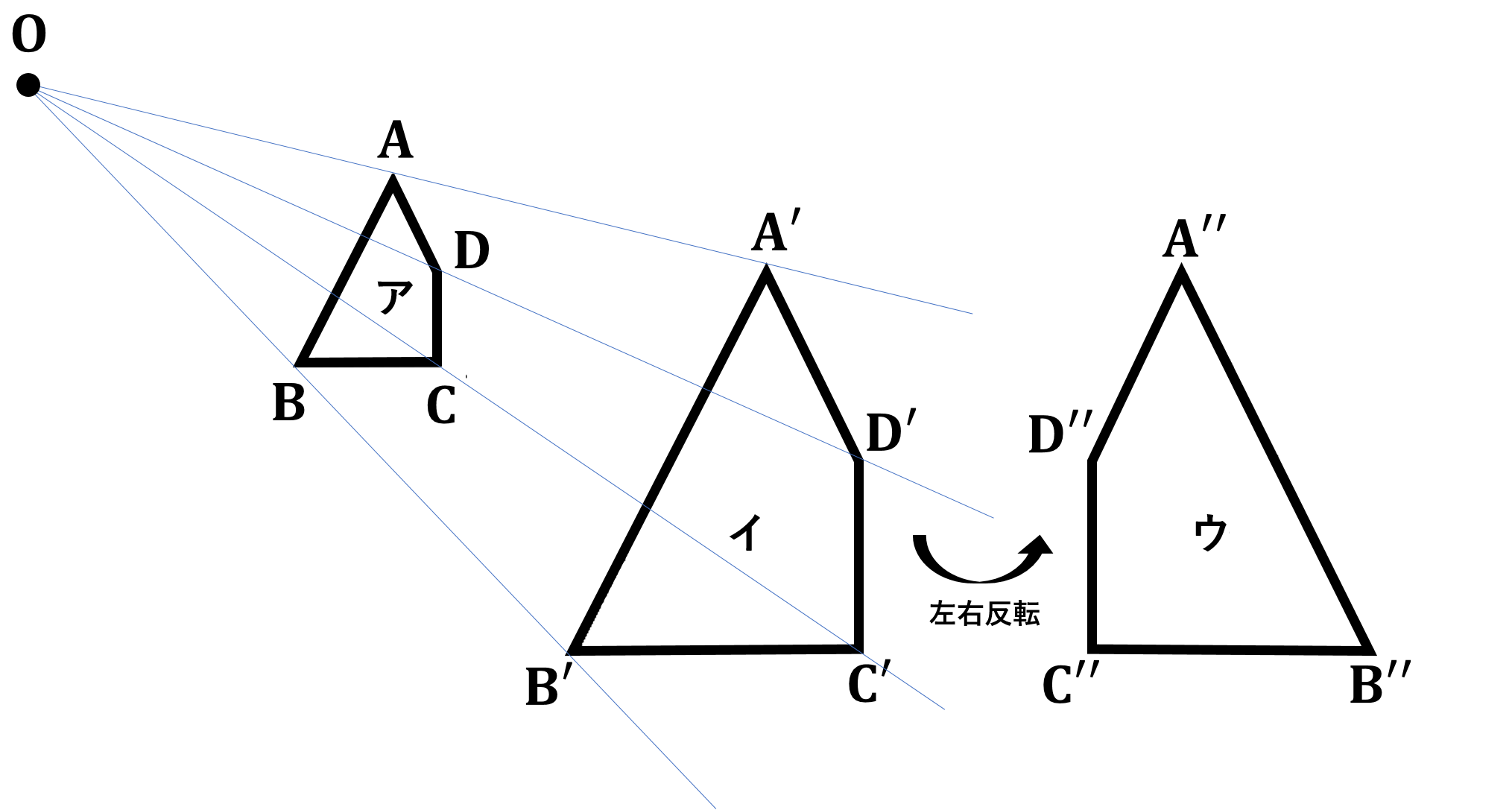
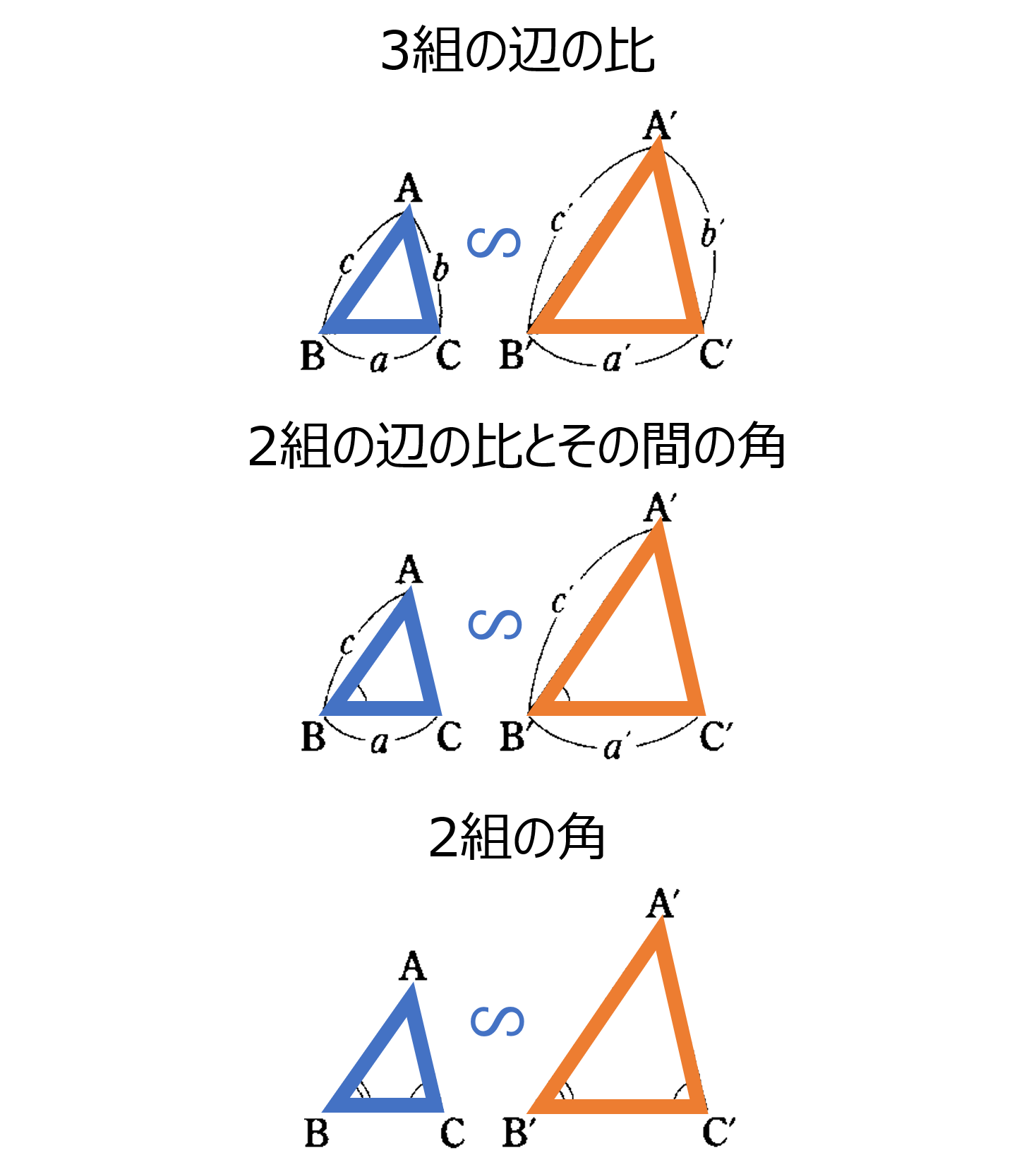
相似な図形で対応する部分の長さの比を相似比といいます。例えば、相似な2つの円では、その相似比は半径の比と等しくなります。続いて三角形の相似条件についてですが、2つの三角形において (1) 3組の辺の比が全て等しい (2) 2組の辺の比とその間の角がそれぞれ等しい (3) 2組の角がそれぞれ等しい のいずれかが成り立つときに相似であるといえます。この相似条件は、2年で学んだ合同条件と比較しながらみてみると、理解や暗記がしやすくなります。
次に三角形と比の定理についてみていきます。下の図の ${\rm \triangle{ABC}}$ の辺 ${\rm AB,AC}$ 上の点をそれぞれ ${\rm D,E}$ とするとき (1) ${\rm DE}/ \! \! /{\rm BC}$ ならば ${\rm AD:AB=AE:AC=DE:BC}$ (2) ${\rm DE}/ \! \! /{\rm BC}$ ならば ${\rm AD:DB=AE:EC}$ が成り立ちます。
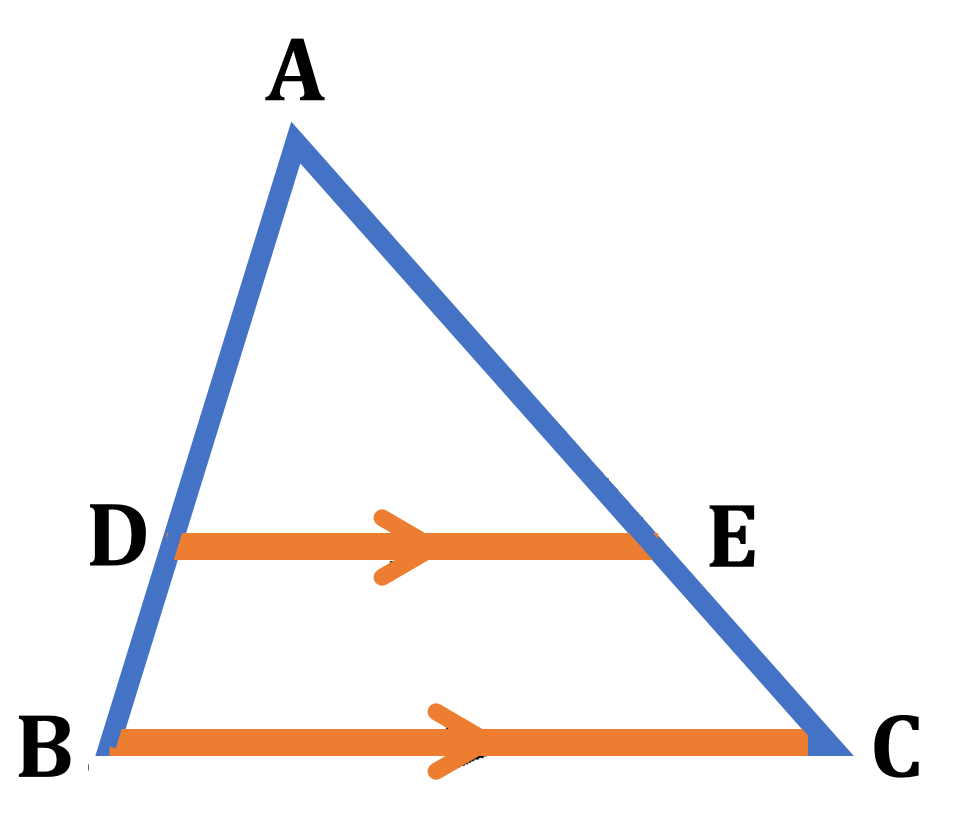
最後に、三角形の比の定理の逆が成り立つかどうかを考えてみましょう。下の図の ${\rm \triangle{ABC}}$ において、辺 ${\rm AB,AC}$ 上に ${\rm AD:AB=AE:AC}$ となるように点 ${\rm D,E}$ をとると ${\rm DE}/ \! \! /{\rm BC}$ となることを証明できれば、三角形の比の定理(1)の逆が成り立つといえます。
${\rm \triangle{ADE}}$ と ${\rm \triangle{ABC}}$ において
仮定から ${\rm AD:AB=AE:AC}$・・・①
また ${\rm \angle A}$ は共通・・・②
①②より、2組の辺の比とその間の角がそれぞれ等しいから
${\rm \triangle{ADE}} ∽ {\rm \triangle{ABC}}$
したがって
${\rm \angle ADE} ∽ {\rm \angle ABC}$
同位角が等しいから
${\rm DE}/ \! \! /{\rm BC}$
よって三角形の比の定理の逆が成り立つことが確かめられました。
定理(2)の逆の証明は割愛しますが、各自で確認しておきましょう。よって、まとめると三角形と比の定理の逆は次のようになります。${\rm \triangle{ABC}}$ の辺 ${\rm AB,AC}$ 上の点をそれぞれ ${\rm D,E}$ とするとき (1) ${\rm AD:AB=AE:AC}$ ならば ${\rm DE}/ \! \! /{\rm BC}$ (2) ${\rm AD:DB=AE:EC}$ ならば ${\rm DE}/ \! \! /{\rm BC}$ が成り立ちます。
相似:2つの図形の一方を拡大または縮小した図形が他方と合同になるとき $\to$ 2つの図形は相似である。
(1) 対応する線分の長さの比はすべて等しい。
(2) 対応する角の大きさはそれぞれ等しい。
三角形の相似条件:2つの三角形において:
(1) 3組の辺の比がすべて等しい。$a:a′=b:b′=c:c′$
(2) 2組の辺の比とその間の角がそれぞれ等しい。$a:a′=c:c′,\angle {\rm B}=\angle {\rm B}′$
(3) 2組の角がそれぞれ等しい。$\angle {\rm B}=\angle {\rm B}′, \angle {\rm C}=\angle {\rm C}′$
平行線と線分の比
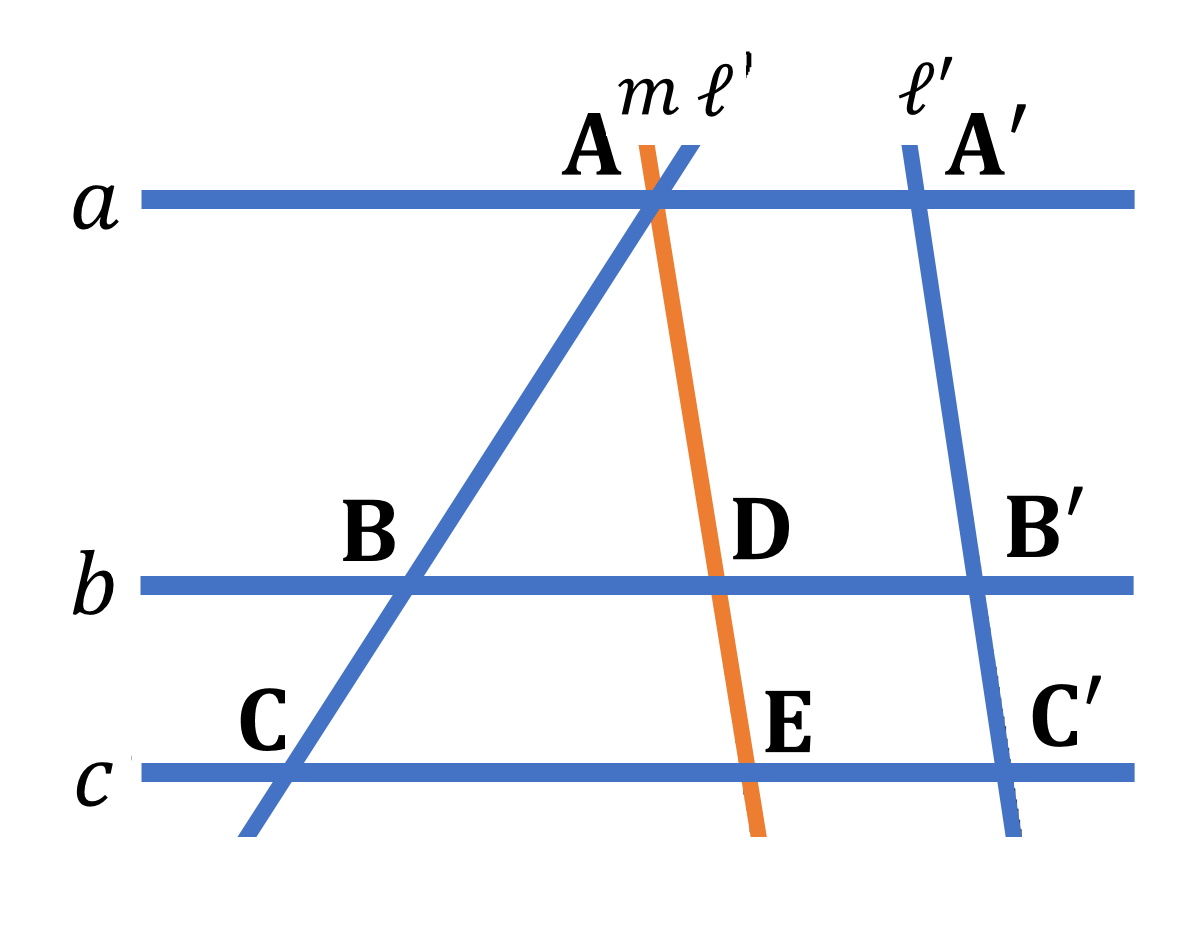
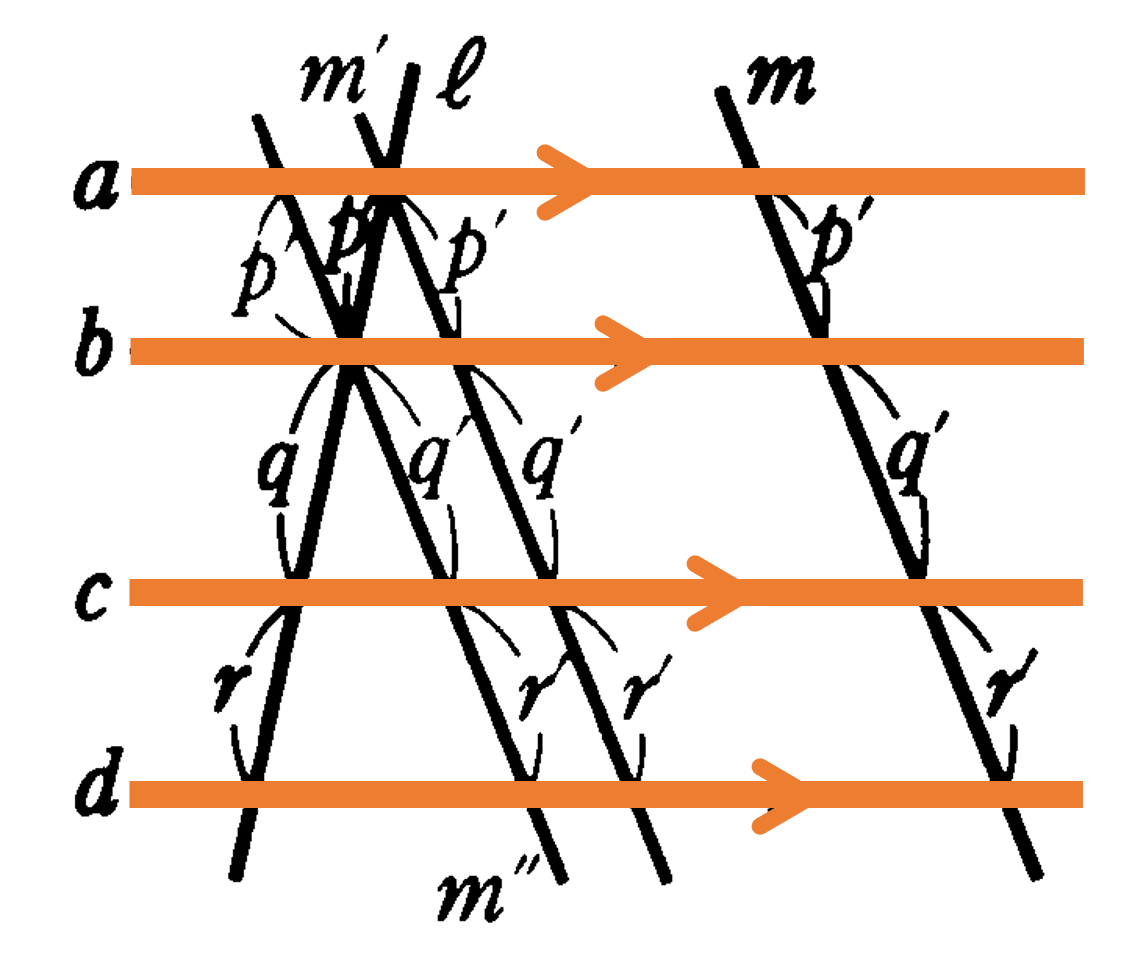
本節では、平行線と比についてみていきましょう。三角形と比の定理から新しい性質を導いていきます。直線が平行線と交わるとき、一般に次の定理が成り立ちます。下の図のように、平行な3つの直線 $a,b,c$ が直線 $\ell$ とそれぞれ ${\rm A,B,C}$ で交わり、直線 $\ell’$ とそれぞれ ${\rm A’,B’,C’}$ で交われば ${\rm AB:BC=A’B’:B’C’}$ が成り立ちます。この定理は以下のように証明できます。
点 ${\rm A}$ を通り $\ell’$ に平行な直線 $m$ をひき、$b,c$ との交点をそれぞれ ${\rm D,E}$ とします。${\rm \triangle{ACE}}$において ${\rm BD}/ \! \! /{\rm CE}$ であるから
${\rm AB:BC=AD:DE}$・・・①
また四角形 ${\rm ADB’A’}$ と四角形 ${\rm DEC’B’}$ はともに平行四辺形であるから
${\rm AD=A’B’, DE=B’C’}$・・・②
①②より
${\rm AB:BC=A’B’:B’C’}$
がいえます。
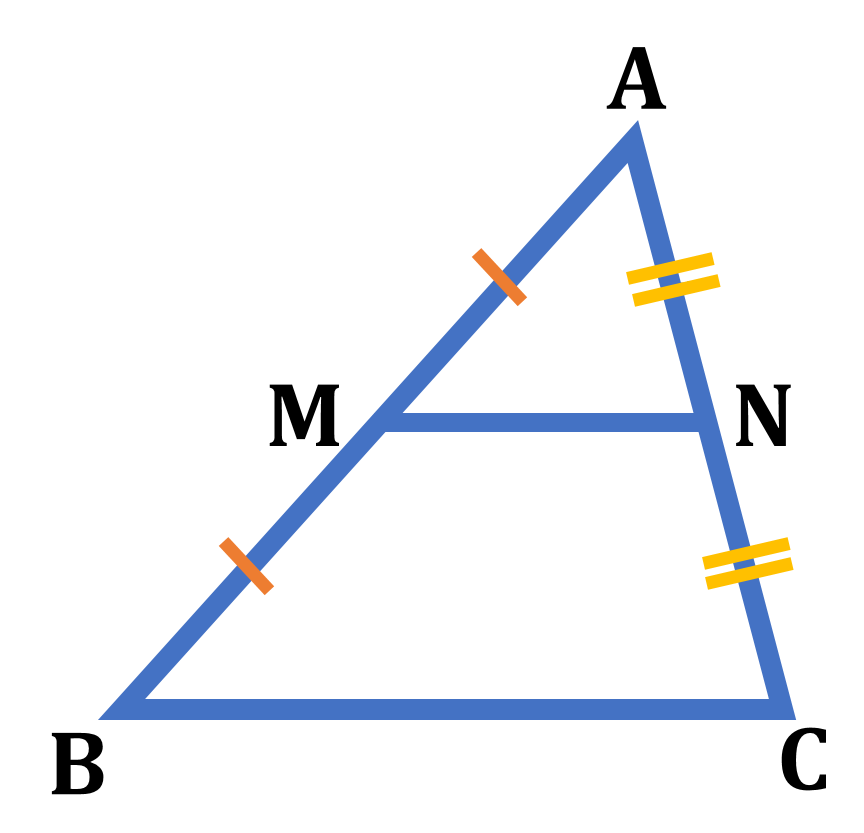
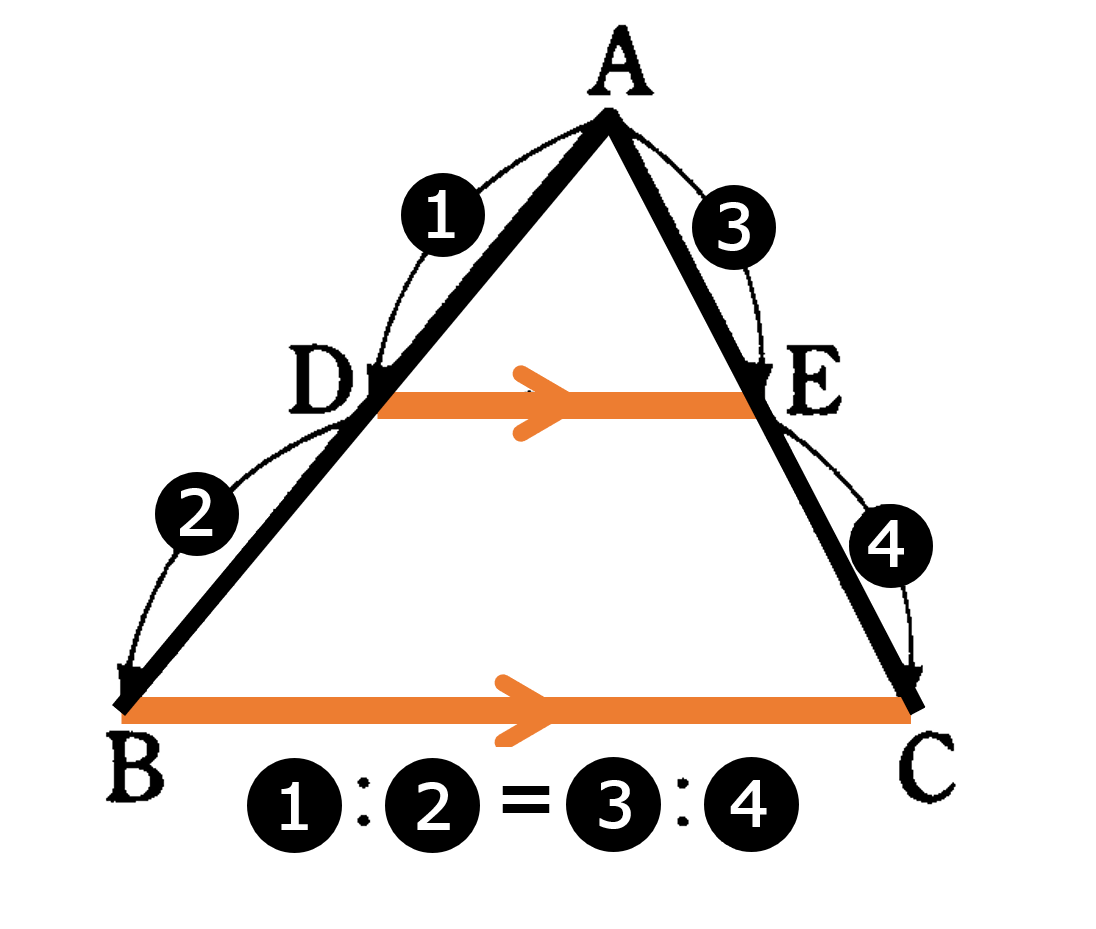
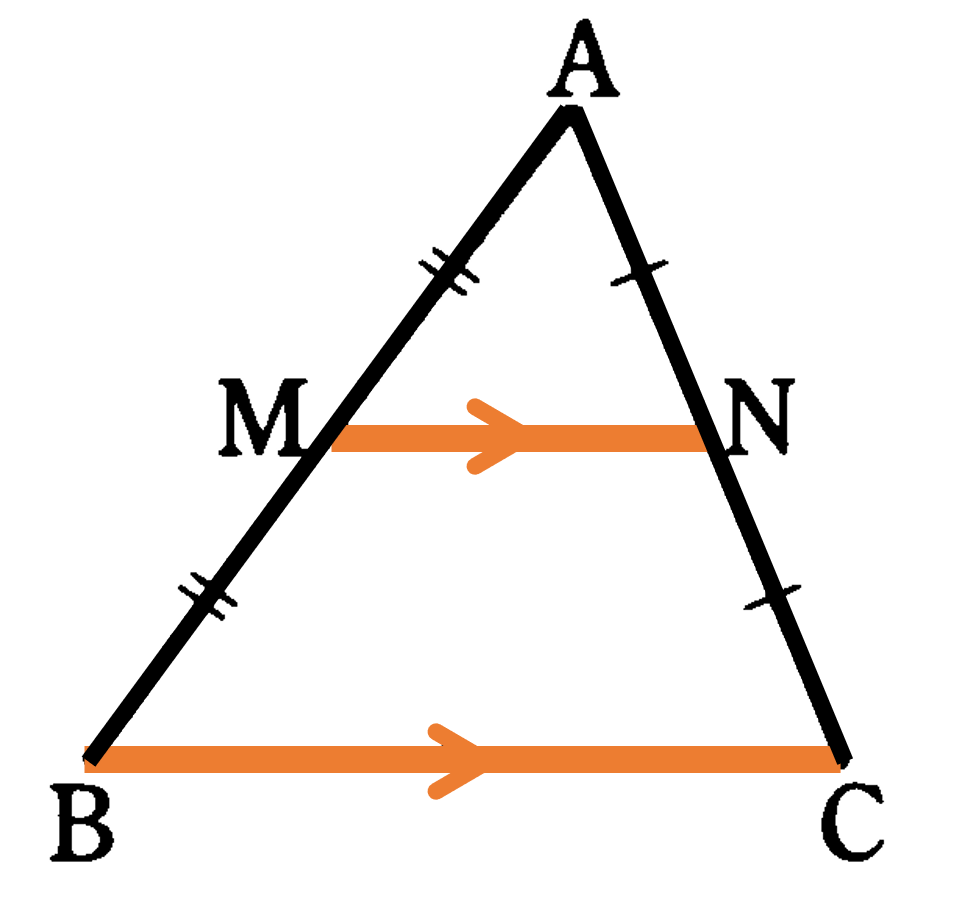
続いて三角形の各辺の中点同士を結んだ線分には、どのような性質があるのかを見てみましょう。下の図の ${\rm \triangle{ABC}}$ の2辺 ${\rm AB,AC}$ の中点をそれぞれ ${\rm M,N}$ とすると ${\rm MN}/ \! \! /{\rm BC}$, ${\rm MN}=\frac{1}{2}{\rm BC}$ という関係が成り立ちます。これは中点連結定理と呼ばれる定理です。
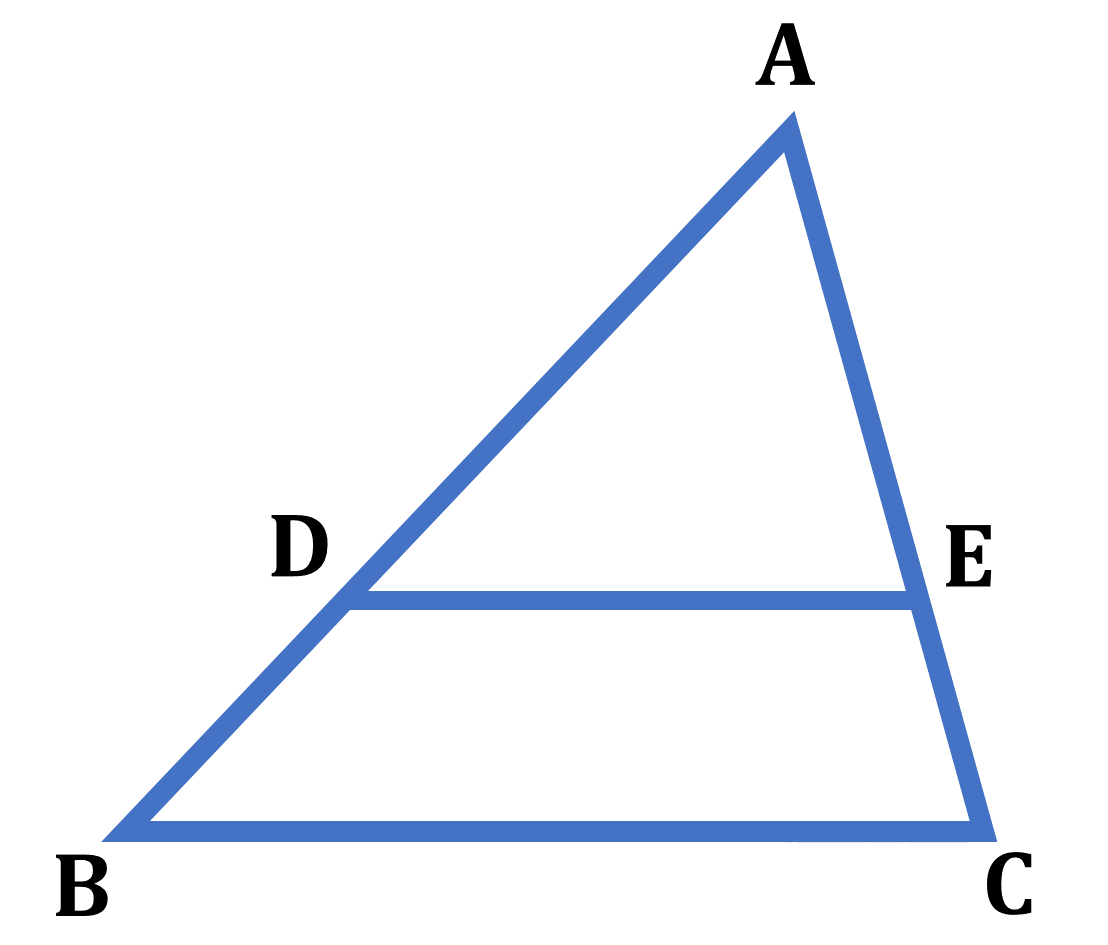
・${\rm \triangle{ABC}}$ で ${\rm DE}/ \! \! /{\rm BC}$ ならば
(1) ${\rm AD}:{\rm AB}$$={\rm AE}:{\rm AC}$$={\rm DE}:{\rm BC}$
(2) ${\rm AD}:{\rm DB}$$={\rm AE}:{\rm EC}$
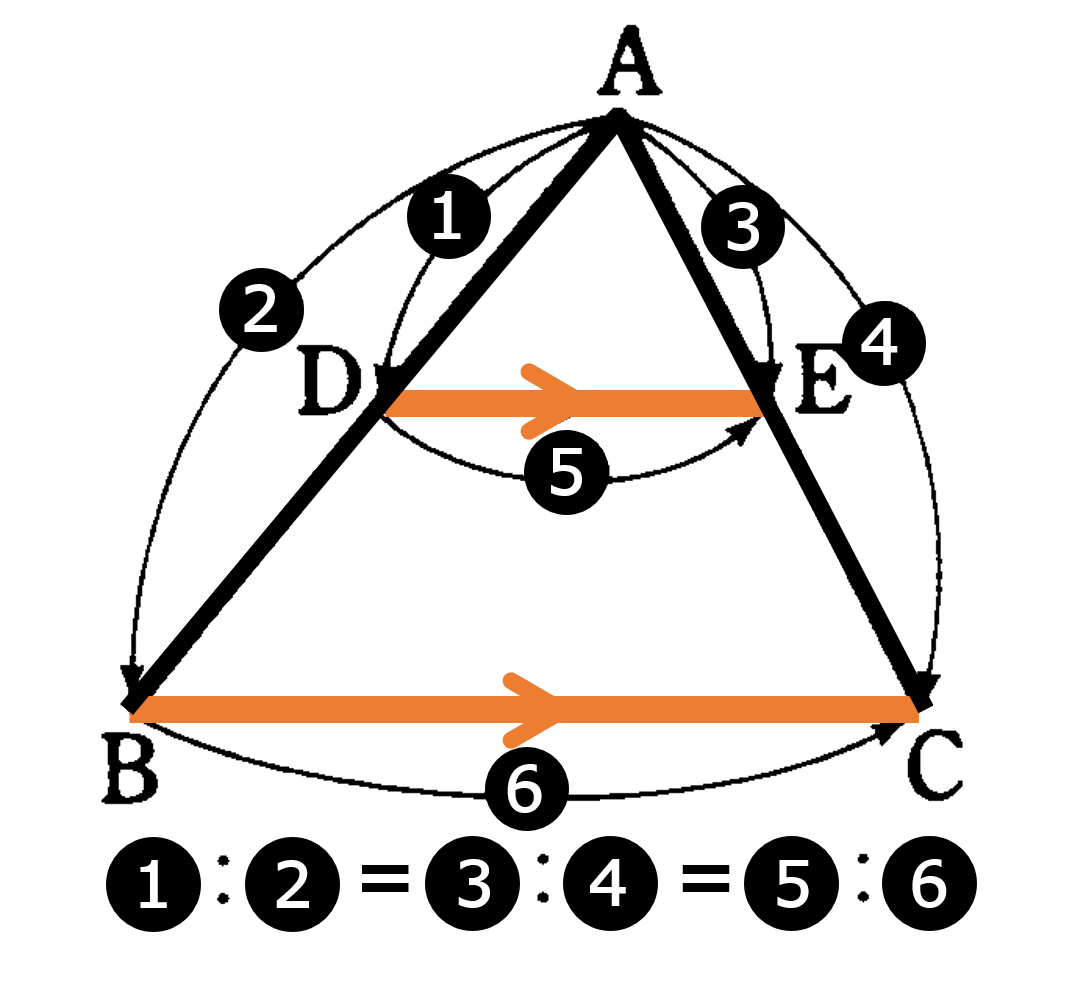
・4直線 $a,b,c,d$ が平行ならば $p:p′=q:q’=r:r’$
${\rm \triangle{ABC}}$の2辺 ${\rm AB},{\rm AC}$ の中点をそれぞれ ${\rm M},{\rm N}$ とすると ${\rm MN}/ \! \! /{\rm BC},{\rm MN}=\frac{1}{2}{\rm BC}$
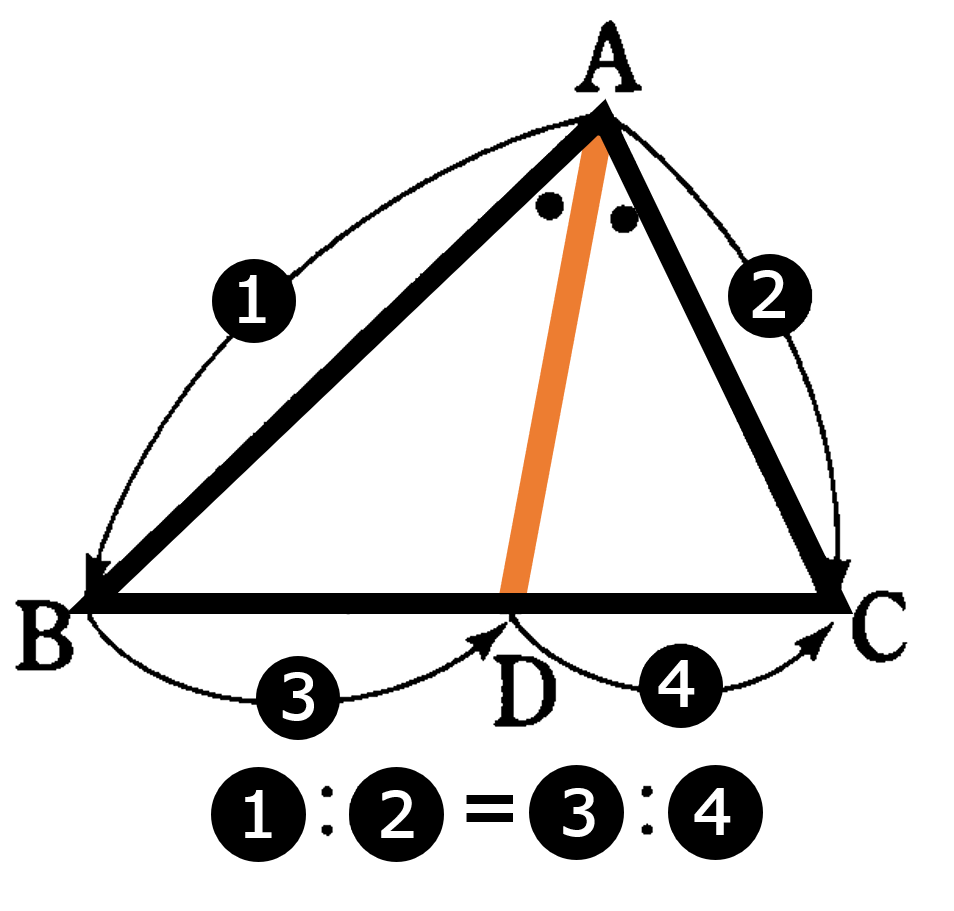
・${\rm \triangle{ABC}}$ の $\angle {\rm A}$ の二等分線 ${\rm AD}$ について ${\rm AB}:{\rm AC}={\rm BD}:{\rm DC}$
相似比と面積比・体積比
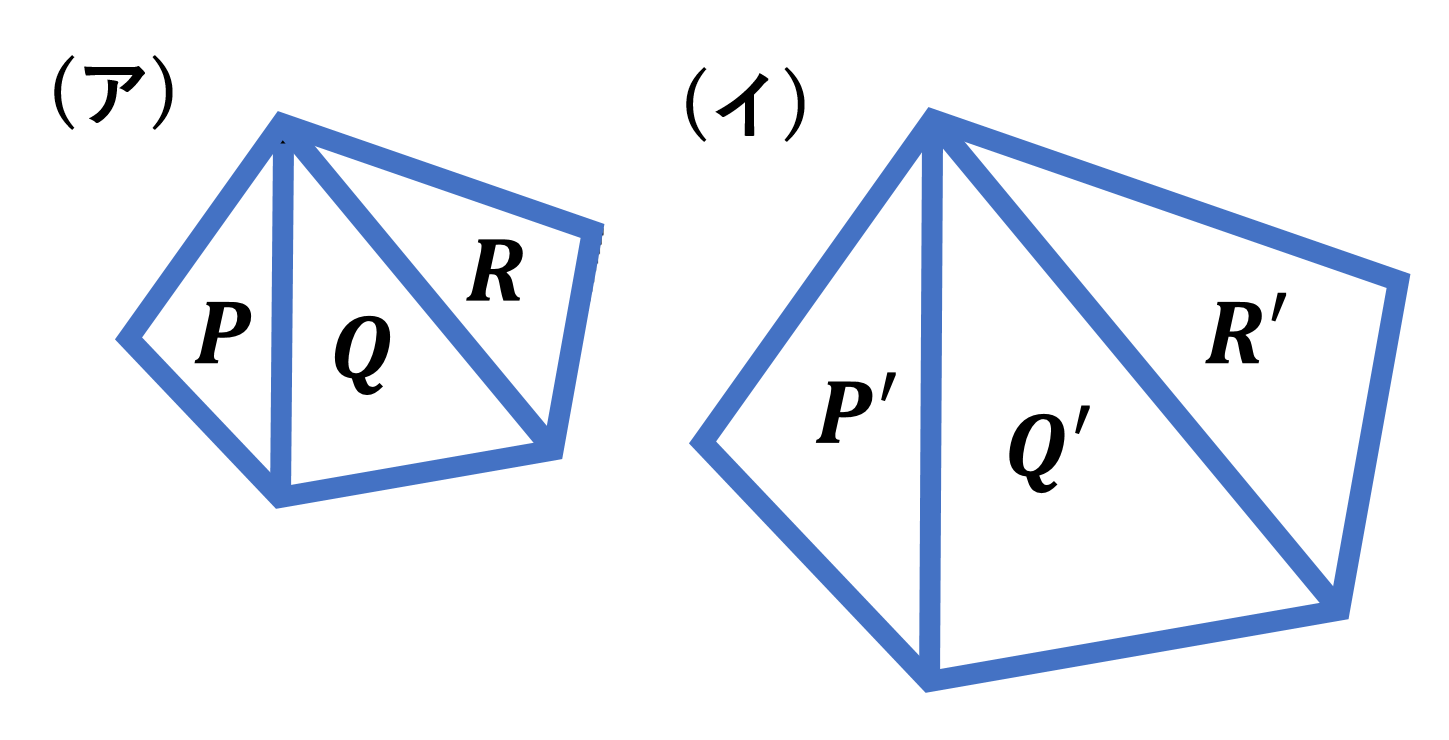
本節では、相似な図形の相似比と面積比についてみていきましょう。一般に、相似な2つの三角形で、その相似比が $m:n$ のとき その面積比は $m^2:n^2$ となります。またこの関係は三角形に限りません。下の図のように、相似な2つの多角形を、対応する頂点から出る対角線で三角形に分けると、対応する三角形はそれぞれ相似になり、相似比はもとの多角形の相似比と同じになります。例えば相似な2つの五角形(ア)(イ)で、その相似比を $2:3$ とすると、対角線で三角形に分けたときに対応する三角形はそれぞれが相似で、その相似比は $2:3$ となります。したがって、対応する三角形の面積比 ${\rm P:P’,Q:Q’,R:R’}$ は全て $2^2:3^2=4:9$ となります。つまり五角形の面積比も $4:9$ となります。このことから、一般に相似な2つの多角形で、その相似比が $m:n$ であるとき面積比は $m^2:n^2$ となることが分かります。さらに、相似な平面図形では、周の長さの比は相似比に等しく、面積比は相似比の2乗に等しくなります。
面積と線分の比:三角形の面積について:
(1) 等底なら高さの比に等しい。
(2) 等高なら底辺の比に等しい。
これらのことは底辺 $b$ 高さ $h$ の三角形の面積 $S$ が $S=\frac{bh}{2}$ であることからも分かる。
(1) 面積比 $\to$ $m^2:n^2$
(2) 体積比 $\to$ $m^3:n^3$
中3 > 6章:円
本章では、円の性質について詳しく調べます。円は1点からの距離が一定である点の集まりであり、たとえば円周上に頂点を持つ角には特別な性質がみられます。このような、円についての様々な性質を調査し、その活用方法や見方を広げていきましょう。
円周角の定理
本節では、円周角の定理について学習します。円 ${\rm O}$ において弧 $\stackrel{\frown}{\rm AB}$ をのぞく円周上の点を $P$ とするとき $\angle {\rm APB}$ を「弧 $\stackrel{\frown}{\rm AB}$ に対する円周角」といいます。また、弧 $\stackrel{\frown}{\rm AB}$ を「円周角 $\angle {\rm APB}$ に対する弧」といいます。
続いて円周角の定理についてみていきましょう。円周角の定理とは「1つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の半分である」というものです。この定理の証明をしましょう。
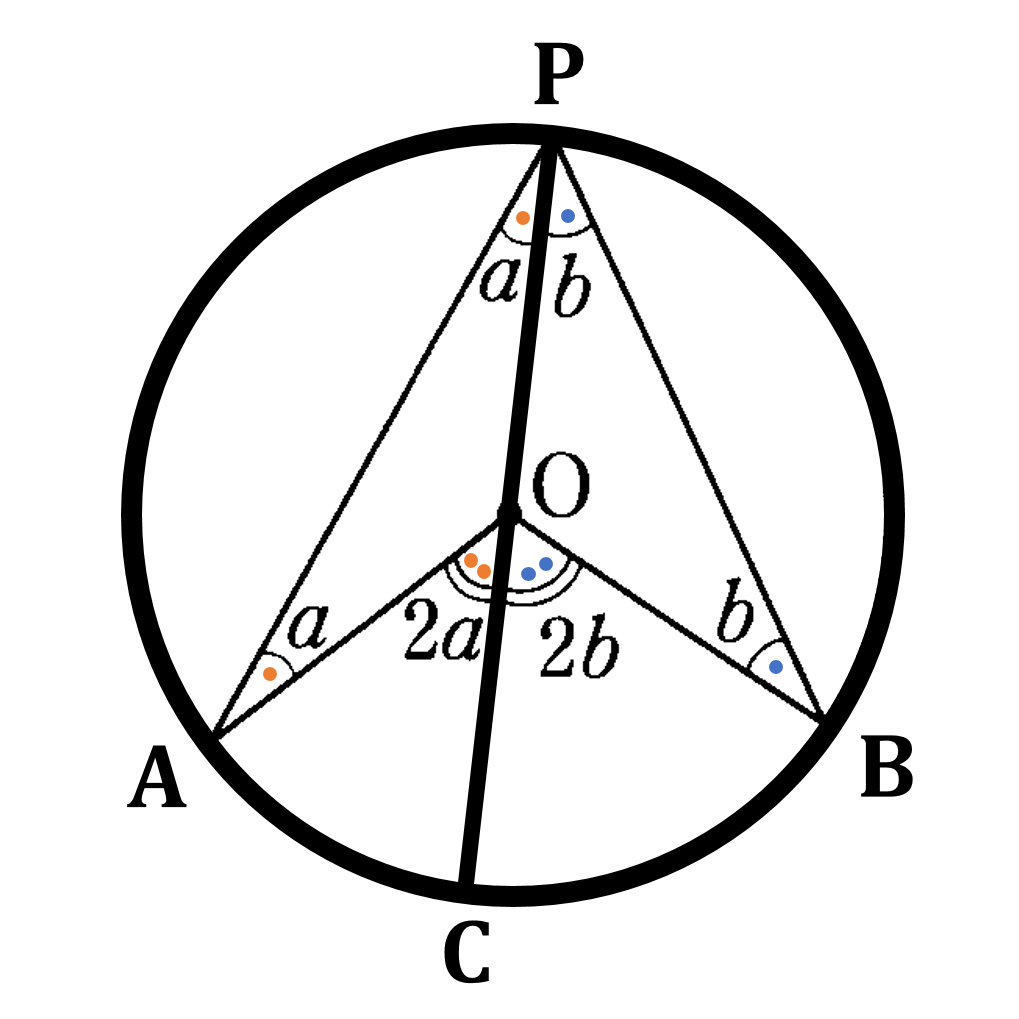
下の図において直径 ${\rm PC}$ をひき $\angle {\rm OPA}=\angle a$, $\angle {\rm OPB}=\angle b$ とします。
${\rm OP=OA}$ であるから
$\angle {\rm OAP}=\angle a$
$\angle {\rm AOC}$ は ${\rm \triangle{OPA}}$ の外角なので
$\angle {\rm AOC}$$=\angle {\rm OAP}+\angle {\rm OPA}$$=2\angle a$
同様にして
$\angle {\rm BOC}$$=2\angle b$
したがって
$\angle {\rm AOB}$$=2(\angle a + \angle b)$
また
$\angle {\rm APB}$$=\angle a + \angle b$
であるから
$\angle {\rm APB}$$=\frac{1}{2}\angle {\rm AOB}$
弧 $\stackrel{\frown}{\rm AB}$ に対する中心角 $\angle {\rm AOB}$ は1つに定まるため、$\angle {\rm APB}$ の大きさは $\frac{1}{2}\angle {\rm AOB}$ で一定となる。(証明終了)
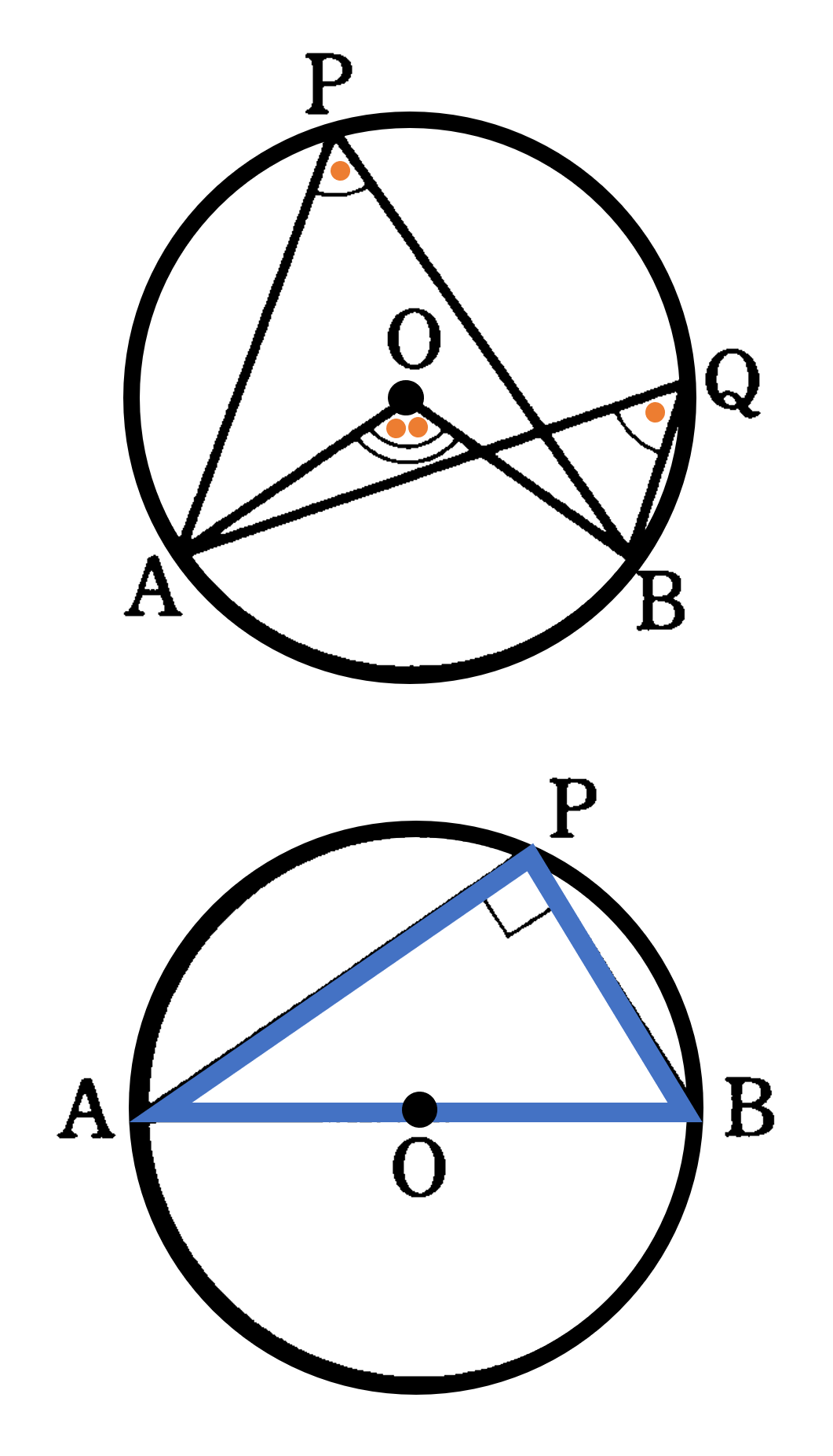
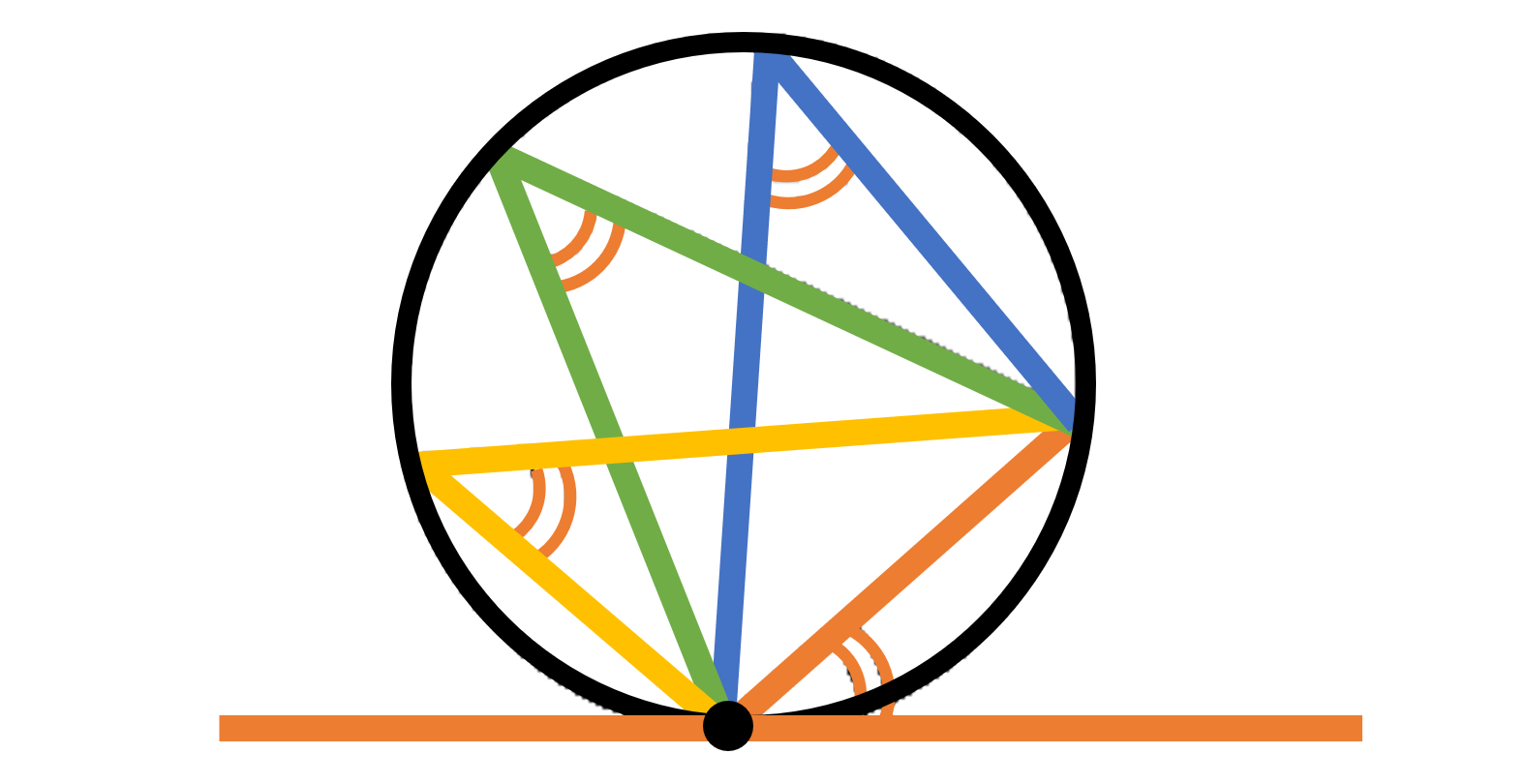
続いて、円周角と弧の性質について、より詳細にみていきましょう。例えば、1つの円で「等しい中心角に対する弧は等しく」なります。逆に「等しい弧に対する中心角も等しく」なります。これらの性質と中心角の定理から、1つの円において「等しい円周角に対する弧は等しく」なり「等しい弧に対する円周角も等しく」なります。また1つの円で「等しい弧に対する弦も等しく」なります。しかしながら、1つの弦に対する弧は2つ存在するため「等しい弦に対する弧は等しい」とはいえないので注意が必要です。
また、直径と円周角の間にも特別な性質があります。半円の弧に対する中心角が $180^{\circ}$ となることから、その円周角は $90^{\circ}$ となります。つまり、線分 ${\rm AB}$ を直径とする円の円周上に、点 ${\rm A,B}$ と異なる点 ${\rm P}$ をとれば $\angle {\rm APB}=90^{\circ}$(直角)となります。この性質の逆も成り立ち、円周上の3点 ${\rm A,P,B}$ について $\angle {\rm APB}=90^{\circ}$(直角)であるならば、線分 ${\rm AB}$ は円の直径になります。
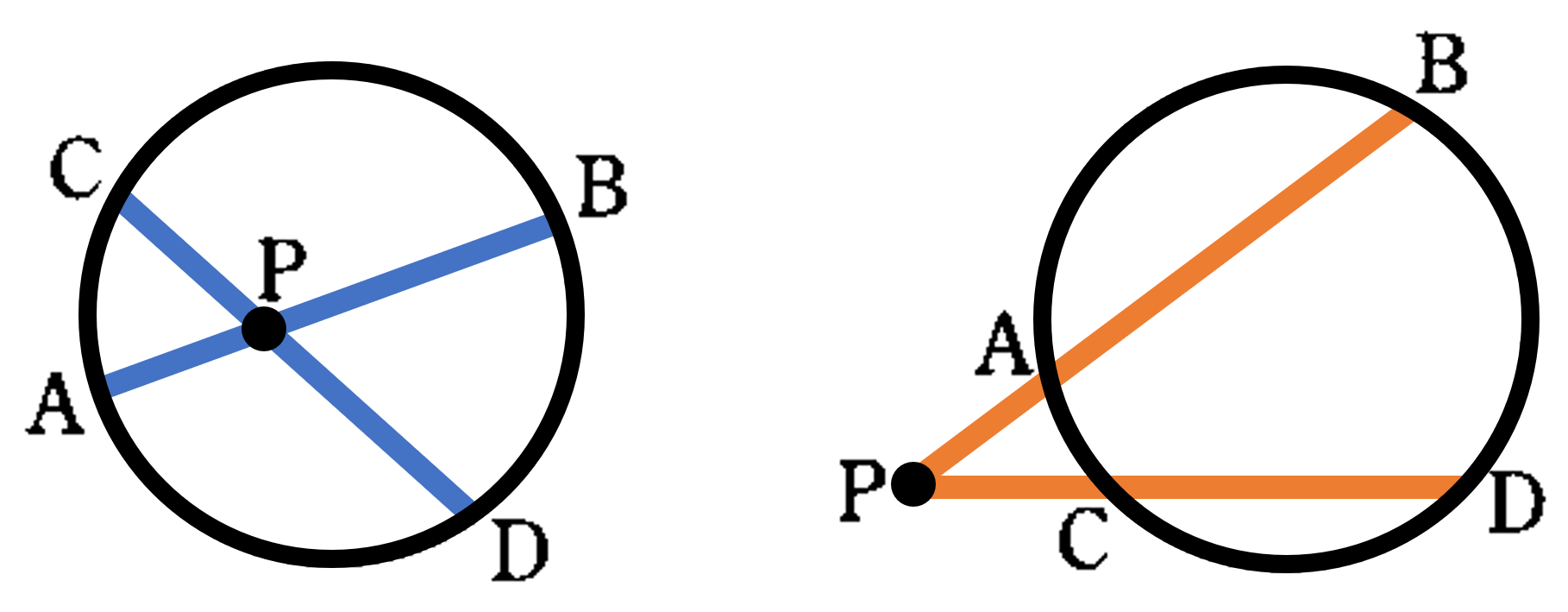
最後に、円周角の定理の逆について考えてみましょう。円周角の定理の逆は、下の図において「4点 ${\rm A,B,P,Q}$ について点 ${\rm P,Q}$ が直線 ${\rm AB}$ の同じ側にあり $\angle {\rm APB}=\angle {\rm AQB}$ ならば、この4点は1つの円周上にある」という性質になります。以下に、この性質が成り立つことを簡単に説明します。
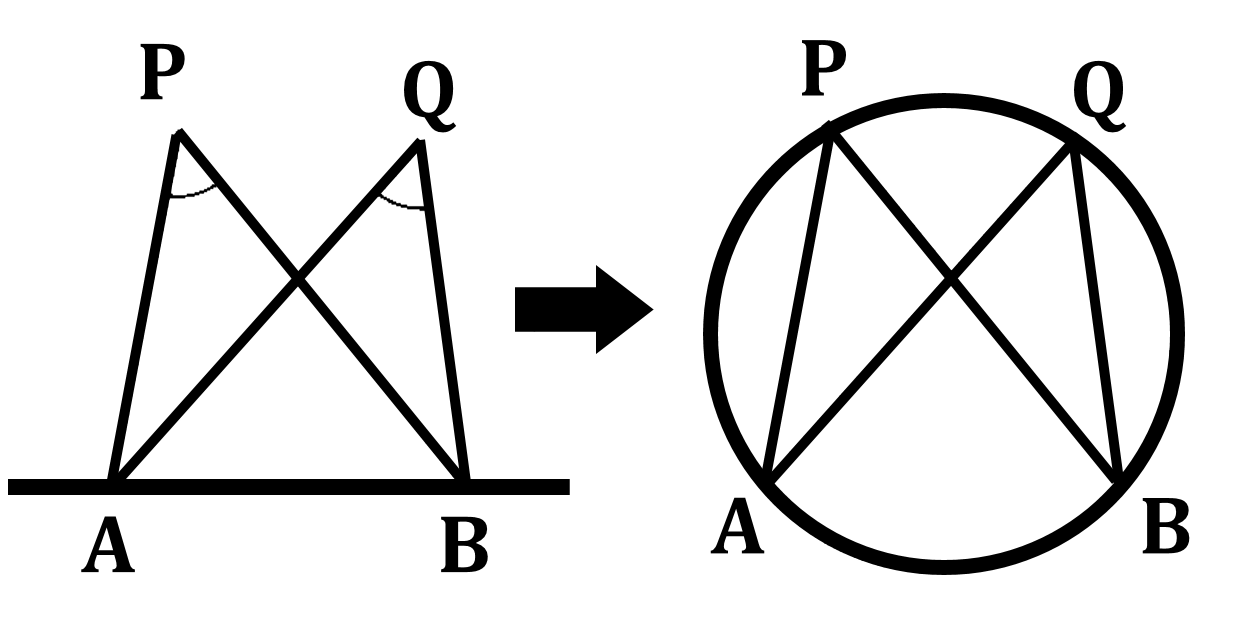
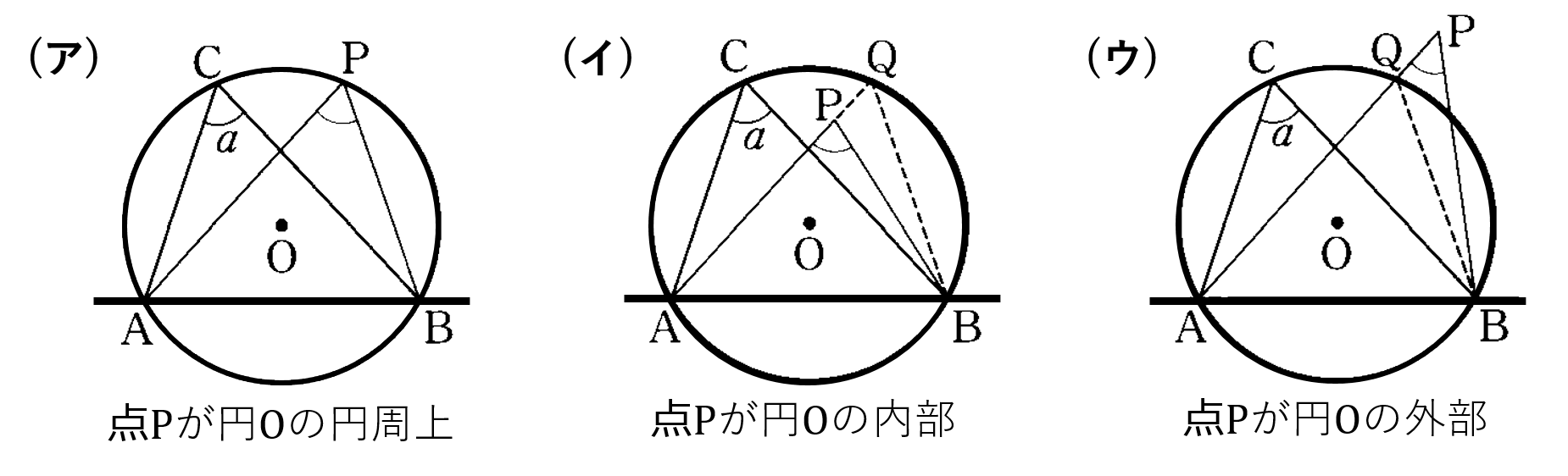
下の図のように、点 ${\rm P}$ が円 ${\rm O}$ の円周上や内部、外部にあるときの $\angle {\rm APB}$ と $\angle a$ の大きさを比べます。
(ア) 円周上にある場合
円周角の定理より
$\angle {\rm APB}=\angle a$・・・①
(イ) 内部にある場合
${\rm AP}$ の延長線と円周との交点を ${\rm Q}$ とすると $\angle {\rm APB}$ は $\triangle {\rm PBQ}$ の外角となるため
$\angle {\rm APB} > \angle a$・・・②
(ウ) 外部にある場合
${\rm AP}$ と円周との交点を ${\rm Q}$ とすると $\angle {\rm AQB}$ は $\triangle {\rm QBP}$ の外角となるため
$\angle {\rm APB} < \angle a$・・・②
①②③より、点 ${\rm P}$ を直線 ${\rm AB}$ に対して点 ${\rm C}$ と同じ側にとったとき $\angle {\rm APB}=\angle a$ ならば点 ${\rm P}$ は円 ${\rm O}$ の円周上にあるということが確かめられました。
円周角の定理:
(1) $\angle {\rm APB} = \frac{1}{2} \angle {\rm AOB}$
(2) $\angle {\rm APB} =\angle {\rm AQB}$
(3) ${\rm AB}$ が直径 $\iff$ $\angle {\rm APB}=90^{\circ}$
2点 ${\rm P,Q}$ が直線 ${\rm AB}$ について同じ側にあるとき $\angle {\rm APB}=\angle {\rm AQB}$ ならば4点 ${\rm A,B,P,Q}$ は1つの円周上にある。
円の接線:
(1) 円の接線は接点を通る半径に垂直である。
(2) 円の外の点からこの円にひいた2本の接線の長さは等しい。
円の様々な問題
本節では、円に関する様々な問題について考えていきましょう。色々な性質について要点内にまとめてあるので、確認しておきましょう。ここでは応用問題として、円を利用した $\sqrt{a}$ の長さの線分の描き方についてみていきましょう。
$\sqrt{a}$ の長さの線分は以下の手順で描くことができます。下の図を用いて説明します。
(1) $a$ を2つの数の積で表します。
$a=bc$
(2) $b+c$ を直径とする円を描きます。
(3) 円の直径を $b:c$ に分ける点を ${\rm P}$ とします。
(4) 点 ${\rm P}$ を通る、この直径の垂線をひき、円との交点を ${\rm P,Q}$ とします。これで作図は完了です。線分 ${\rm PQ}$ の長さが $\sqrt{a}$ となるのですが、以下にその証明を示します。
$\triangle {\rm QPA}$ と $\triangle {\rm BPR}$ において
円周角の定理より
$\angle {\rm AQP} = \angle {\rm RBP}$・・・①
対頂角は等しいから
$\angle {\rm QPA} = \angle {\rm BPR}$・・・②
①②より2組の角がそれぞれ等しいから
$\triangle {\rm QPA} ∽ \triangle {\rm BPR}$
よって対応する辺の比は等しいから
${\rm AP:QP=RP:BP}$
${\rm QP \times RP = AP \times BP}$
${\rm QP^2 }= b \times c$
${\rm QP} = \sqrt{bc}$
${\rm QP} = \sqrt{a}$
よって、線分 ${\rm PQ}$ の長さが $\sqrt{a}$ となります。
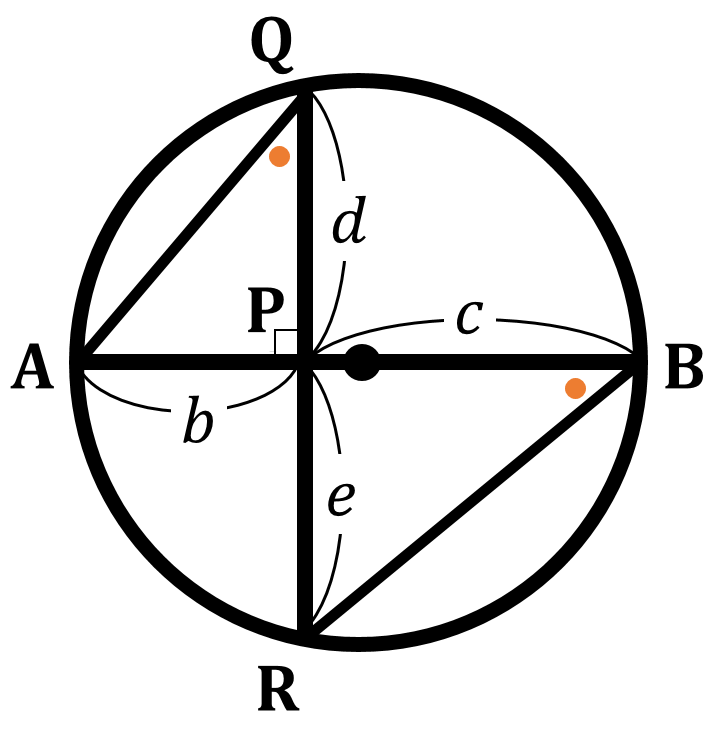
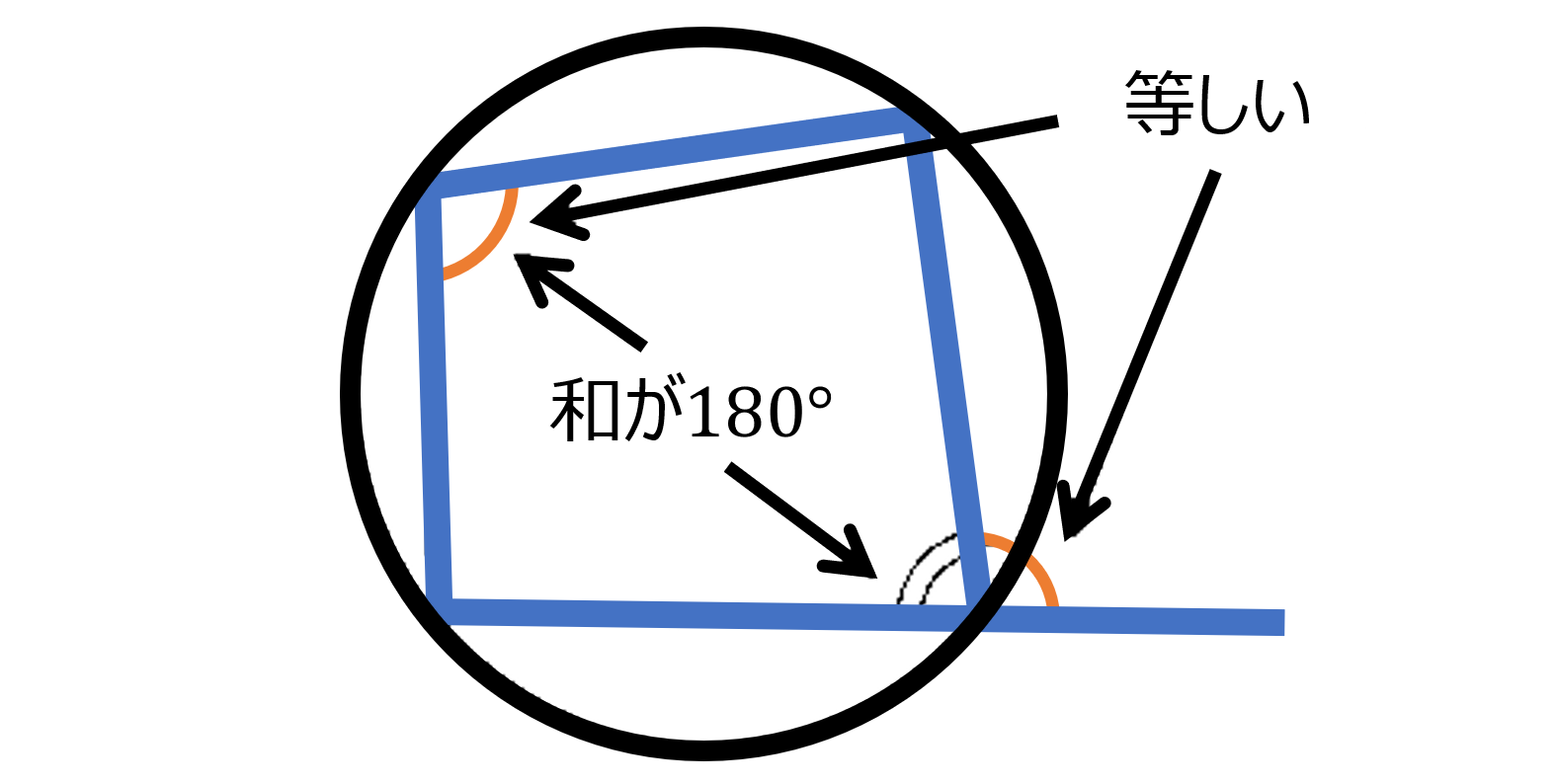
円に内接する四角形 :
(1) 四角形の対角の和は $180^{\circ}$
(2) 四角形の外角はそれと隣り合う内角の対角に等しい。
中3 > 7章:三平方の定理
本章では、三平方の定理について学びます。三平方の定理はピタゴラスの定理ともいい、非常に便利で実用的な定理です。その証明方法や活用方法について学び、いろいろな問題に対して、この定理を利用できるようになりましょう。
三平方の定理
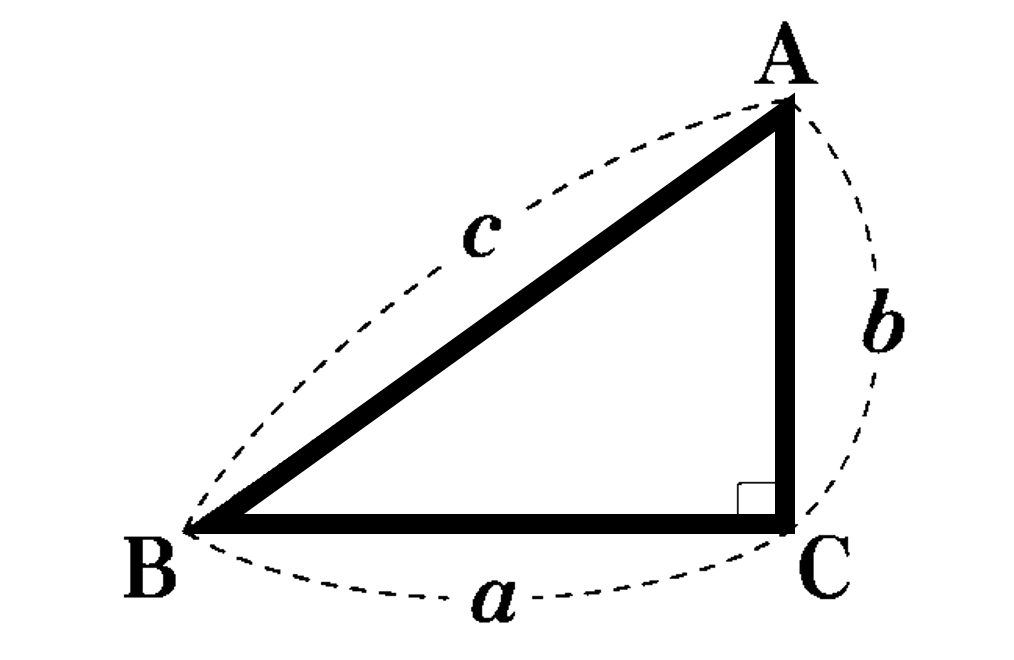
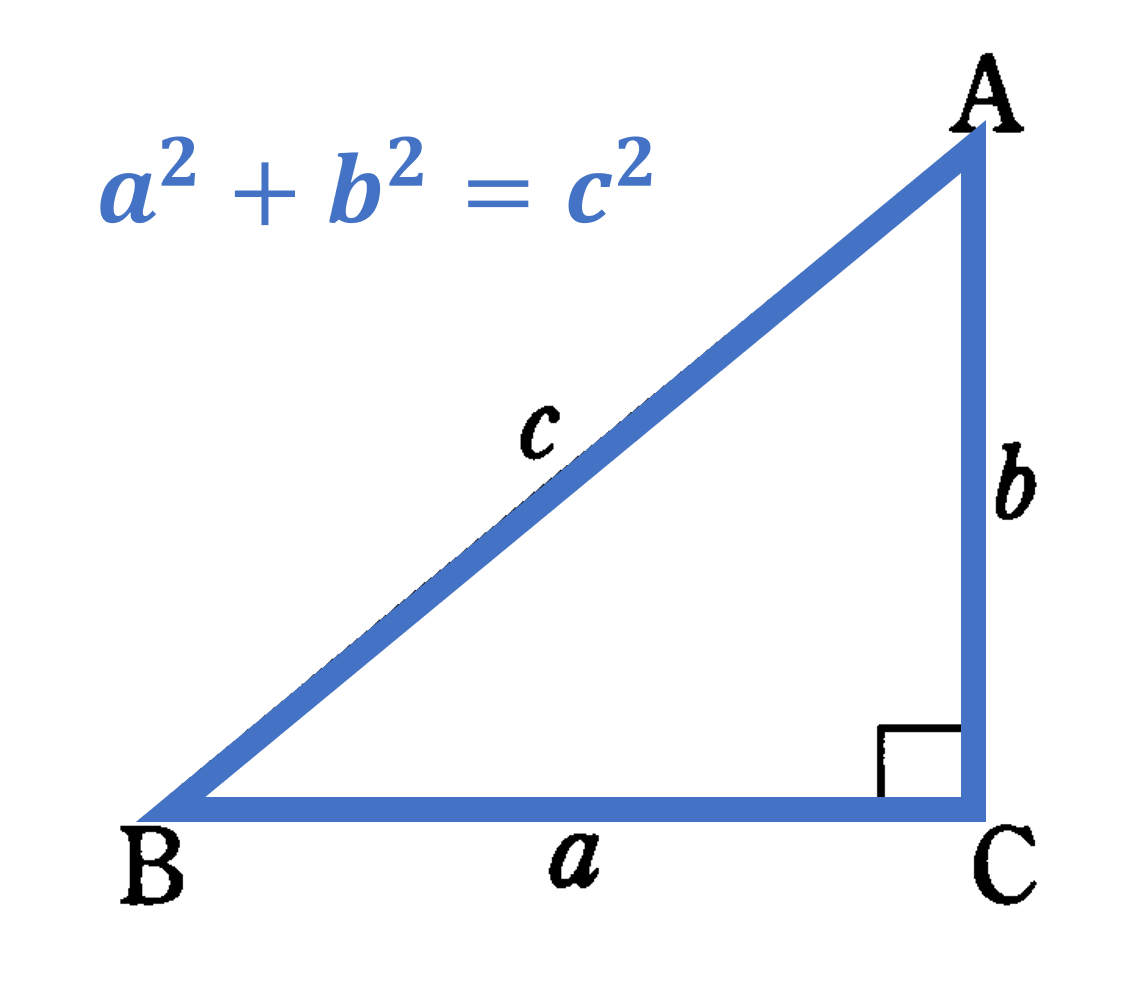
三平方の定理とは「直角三角形の直角をはさむ2辺の長さを $a,b$ 斜辺の長さを $c$ としたときに $a^2+b^2=c^2$ という関係が成り立つ」というものです。この定理は、古代エジプト時代から知られており、ギリシャの数学者であるピタゴラスにちなんでピタゴラスの定理ともよばれます。
下の図のように、直角三角形 $\triangle {\rm ACB}$ と合同な直角三角形を、1辺の長さが $c$ の正方形の周りに描きます。そうすると、外側に1辺が
の長さが $a+b$ の正方形ができます。この図で面積の関係を考えます。(1辺 $c$ の正方形の面積)$=$(1辺 $a+b$ の正方形の面積)$-$($\triangle {\rm ABC}$ の面積)$\times 4$ であるから
\begin{eqnarray}
c^2 &=& (a+b)^2-\frac{1}{2}ab \times 4 \\
&=& (a^2+2ab+b^2)-2ab \\
&=& a^2+b^2
\end{eqnarray}
よって三平方の定理が証明されました。
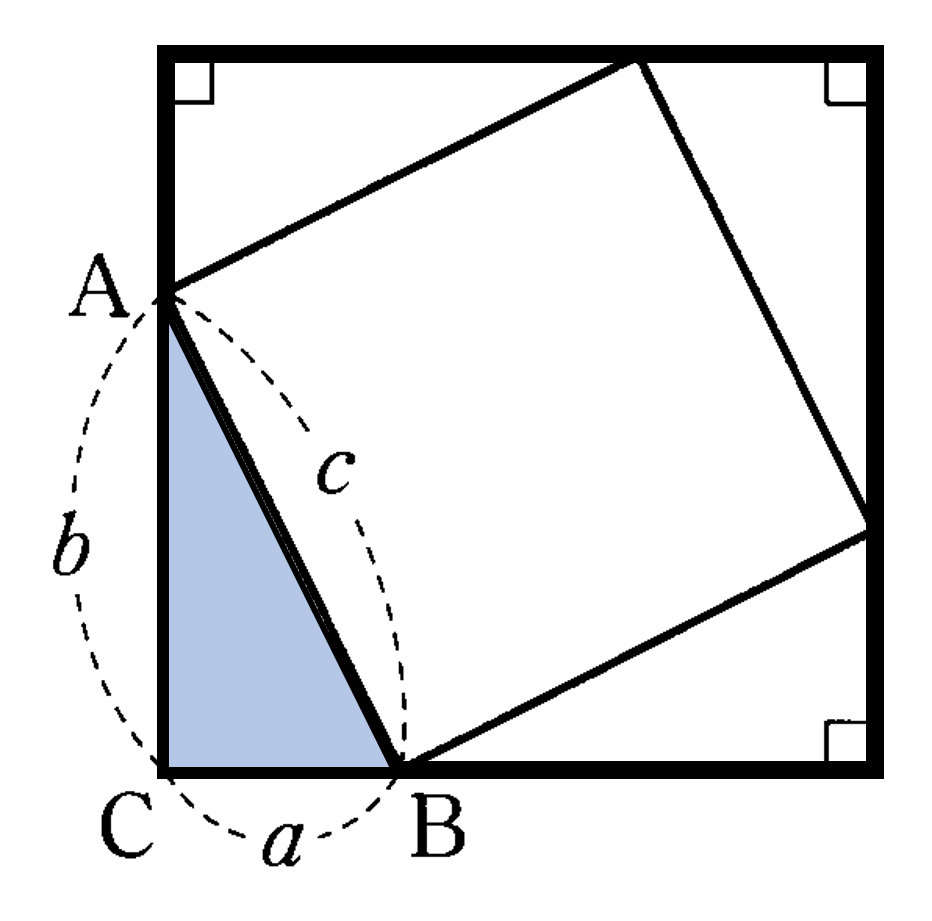
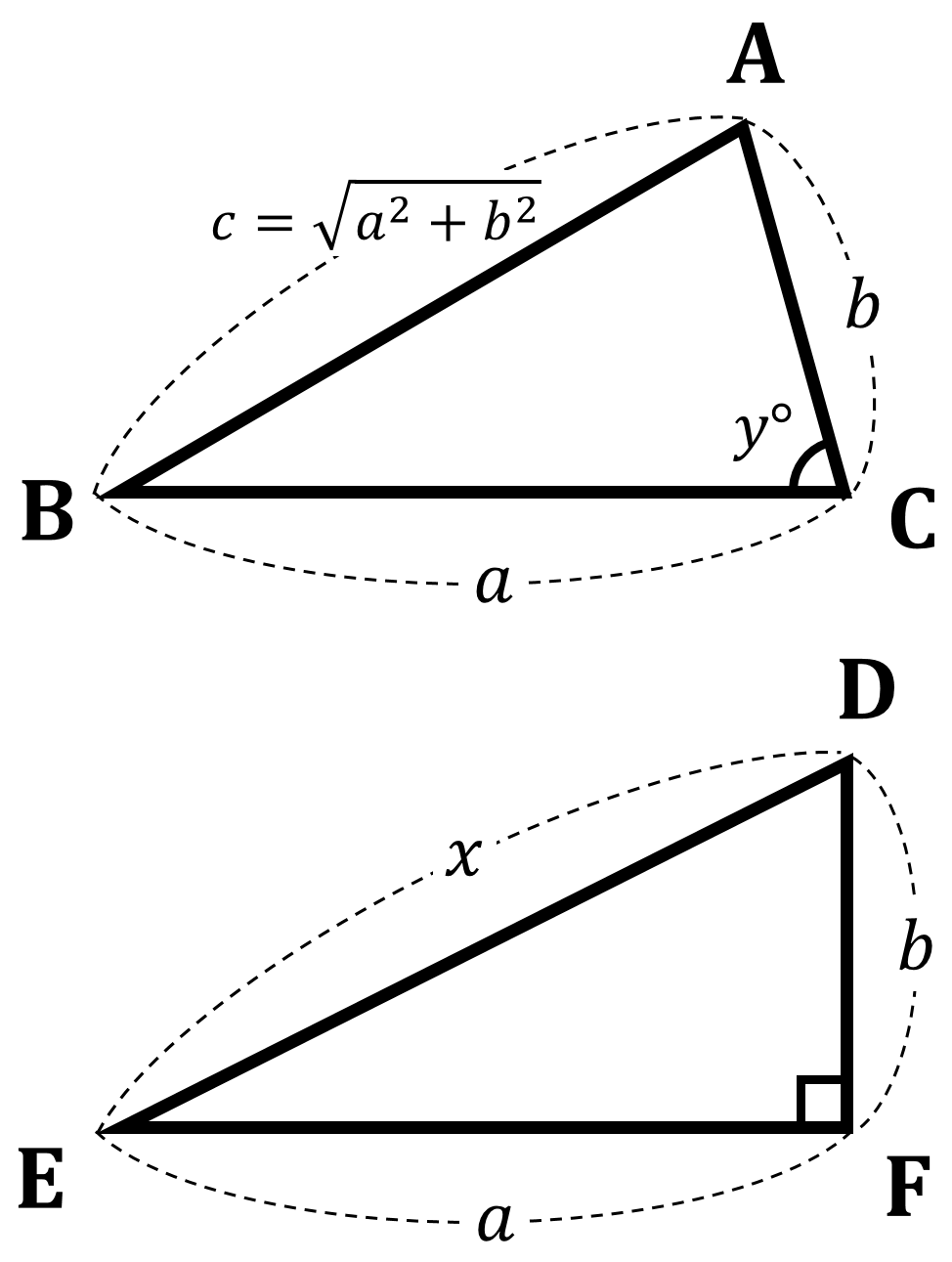
下の図のように ${\rm BC} = a$,${\rm CA} = b$,${\rm AB} = c$ で $a^2+b^2=c^2$ が成り立つ $\triangle {\rm ABC}$ を考えます。この三角形の斜辺に対する角 $\angle {\rm C} = y$ とします。次に ${\rm EF} = a$,${\rm FD} = b$,${\rm DE} = x$, $\angle {\rm F} = 90^{\circ}$ である $\triangle {\rm DEF}$ を考え $\triangle {\rm ABC}$ と比較します。
$\triangle {\rm DEF}$ において三平方の定理より
$a^2+b^2=x^2$・・・①
仮定から
$a^2+b^2=c^2$・・・②
①②より
$x^2=c^2$
$x > 0$,$c > 0$であるから
$x=c$
つまり
${\rm DE} = {\rm AB}$・・・③
仮定より
${\rm EF} = {\rm BC}$・・・④
${\rm FD} = {\rm CA}$・・・⑤
③④⑤より
$\triangle {\rm ABC}$ と $\triangle {\rm DEF}$ において3組の辺がそれぞれ等しいため
$\triangle {\rm ABC} ≡ \triangle {\rm DEF}$
したがって対応する角の大きさは等しいので
$\angle {\rm C} = \angle {\rm F}$
$y=90^{\circ}$
よって三平方の定理の逆が成り立つことが証明できました。
三平方の定理:直角三角形の直角をはさむ2辺の長さを $a$, $b$ 斜辺の長さを $c$ とすると $a^2+b^2=c^2$ が成り立つ。
数学が面白くなる動画―17
三平方の定理の証明方法を考えてみましょう。
3辺の長さが $a,b,c$ である三角形において $a^2+b^2=c^2$ が成り立つならばその三角形は長さ $c$ の辺を斜辺とする直角三角形である。
三平方の定理の利用
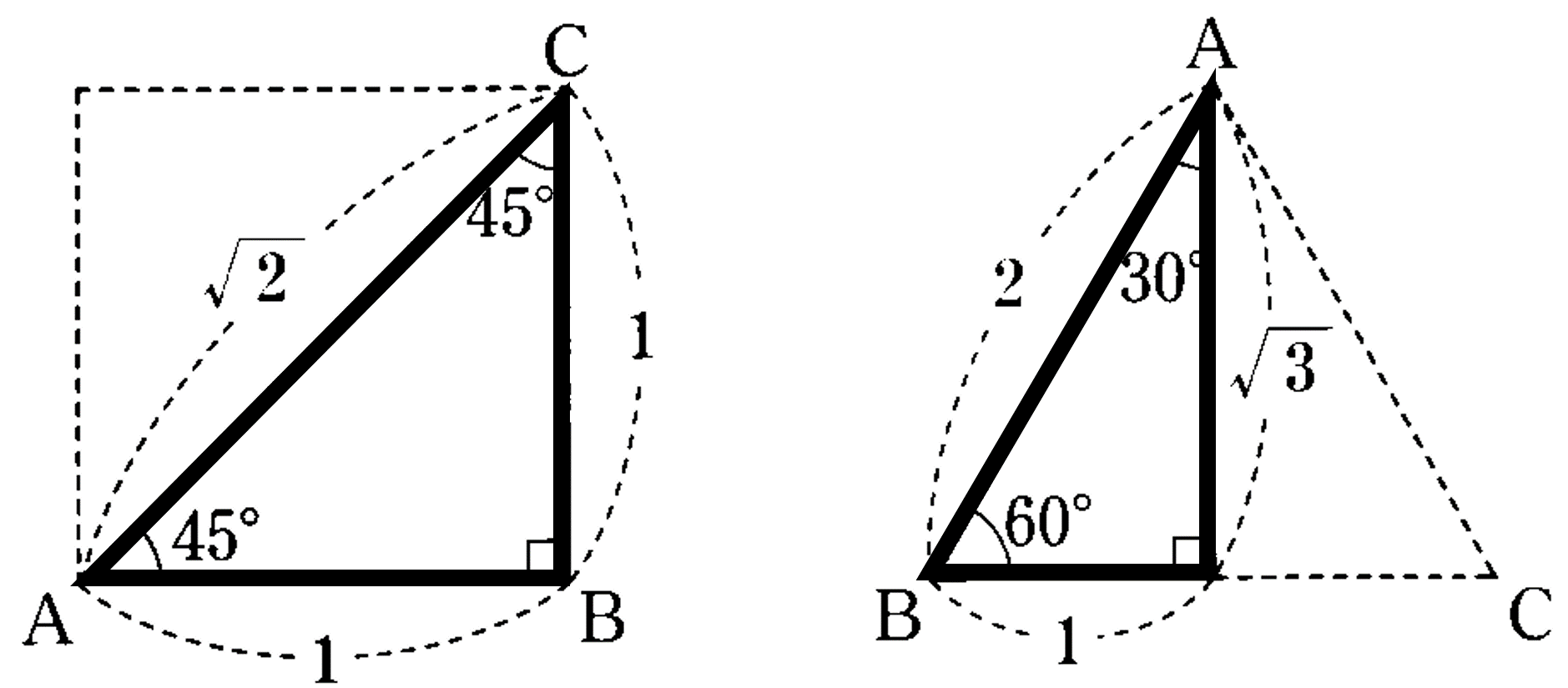
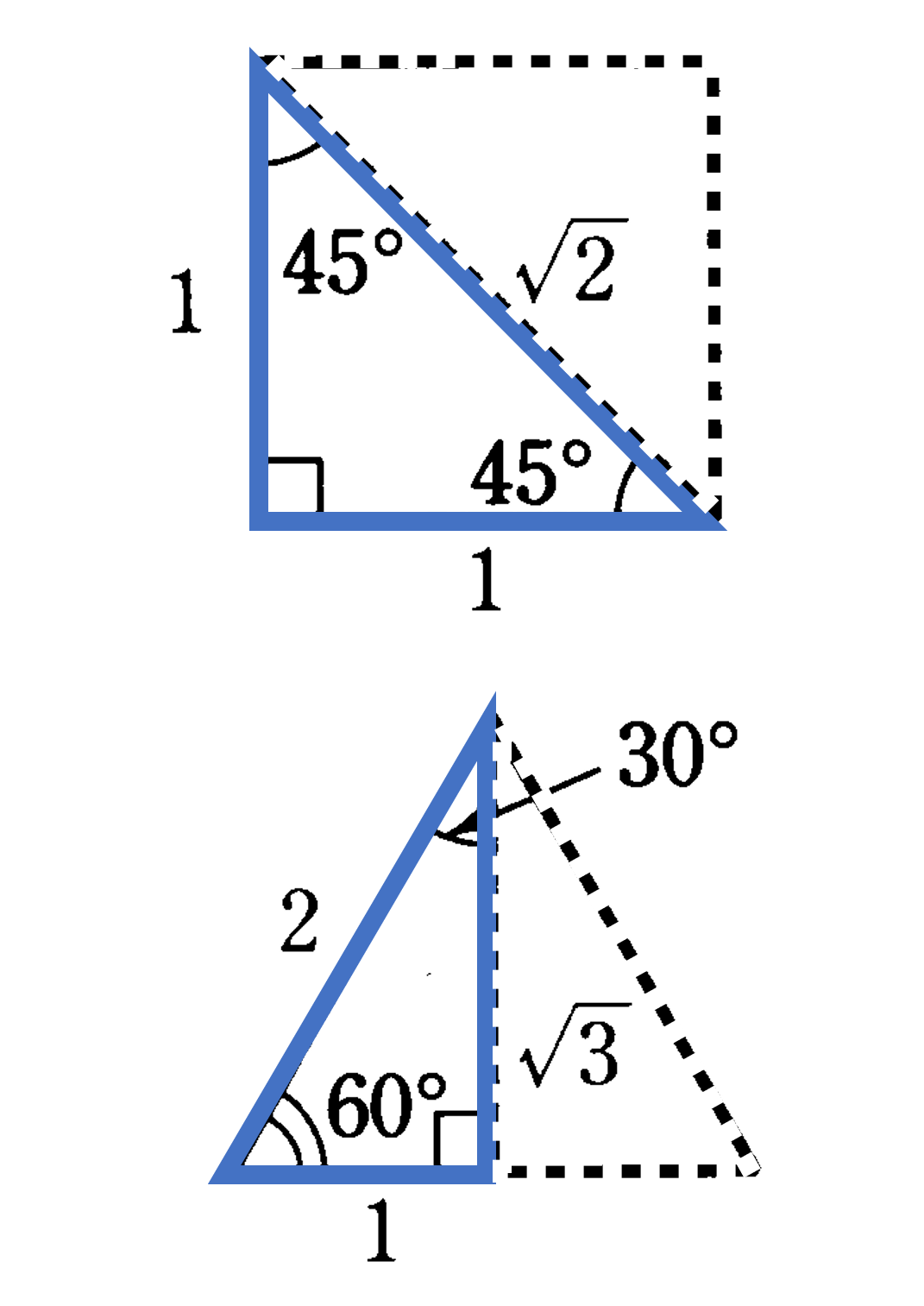
本節では、三平方の定理を利用して、いろいろな長さを求める方法について考えてみましょう。例えば特徴的な直角三角形として、3つの角が$45^{\circ}$, $45^{\circ}$, $90^{\circ}$ である直角三角形と $30^{\circ}$, $60^{\circ}$, $90^{\circ}$ である直角三角形の3辺の長さは、下図のような関係が成り立っています。この関係は非常に重要で、問題にもよく利用されますので、正しく理解しておきましょう。
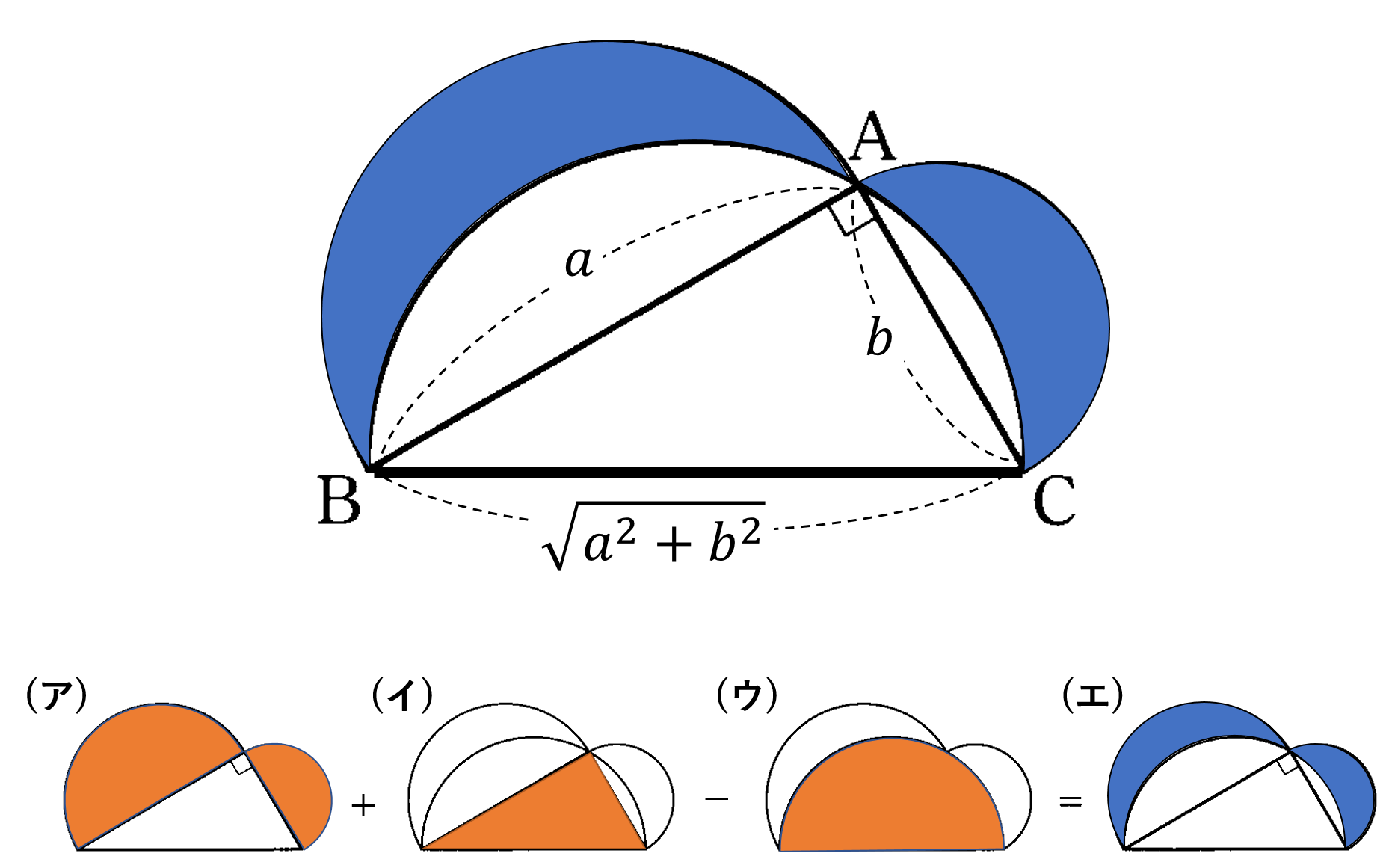
ヒポクラテスの月形の面積(エ)は、下の図のように(ア)$+$(イ)$-$(ウ)という計算で求めることができます。
\begin{eqnarray}
(ア)&=&\pi a^2 \times \frac{1}{2}+\pi b^2 \times \frac{1}{2}\\
&=&\frac{1}{2}\pi(a^2+b^2) ・・・①\\
\\
(イ)&=&\frac{1}{2}ab ・・・②
\\
(ウ)&=&\pi (\sqrt{a^2+b^2})^2 \times \frac{1}{2}\\
&=&\frac{1}{2}\pi(a^2+b^2) ・・・③
\end{eqnarray}
①②③より
\begin{eqnarray}
(エ)&=&(ア)+(イ)-(ウ)\\
&=&\frac{1}{2}\pi(a^2+b^2)+\frac{1}{2}ab\\
& &-\frac{1}{2}\pi(a^2+b^2)\\
&=&\frac{1}{2}ab
\end{eqnarray}
となり、ヒポクラテスの月形の面積は、直角三角形 $\triangle {\rm ABC}$ の面積と等しくなることが分かります。
このように、三平方の定理を学ぶことで、一見複雑な図形の面積も求めることができるようになります。応用範囲の広い「三平方の定理」を是非、正しく理解しておきましょう。
特別な直角三角形の3辺の長さの比:
(1) 直角二等辺三角形 $\to$ $1:1:\sqrt{2}$
(2) $30^{\circ},60^{\circ}$ の直角三角形 $\to$ $1:2:\sqrt{3}$
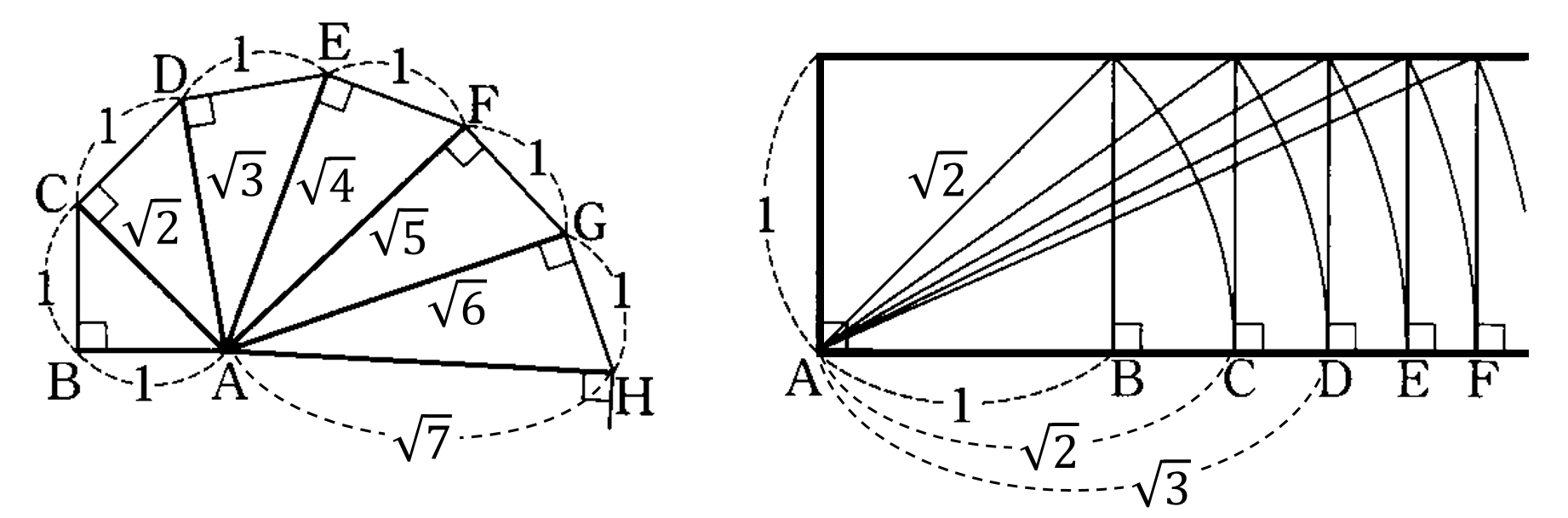
2点 ${\rm A},{\rm B}$ 間の距離は ${\rm AB}$$=\sqrt{(x\small{座標の差})^2+(y\small{座標の差})^2}$
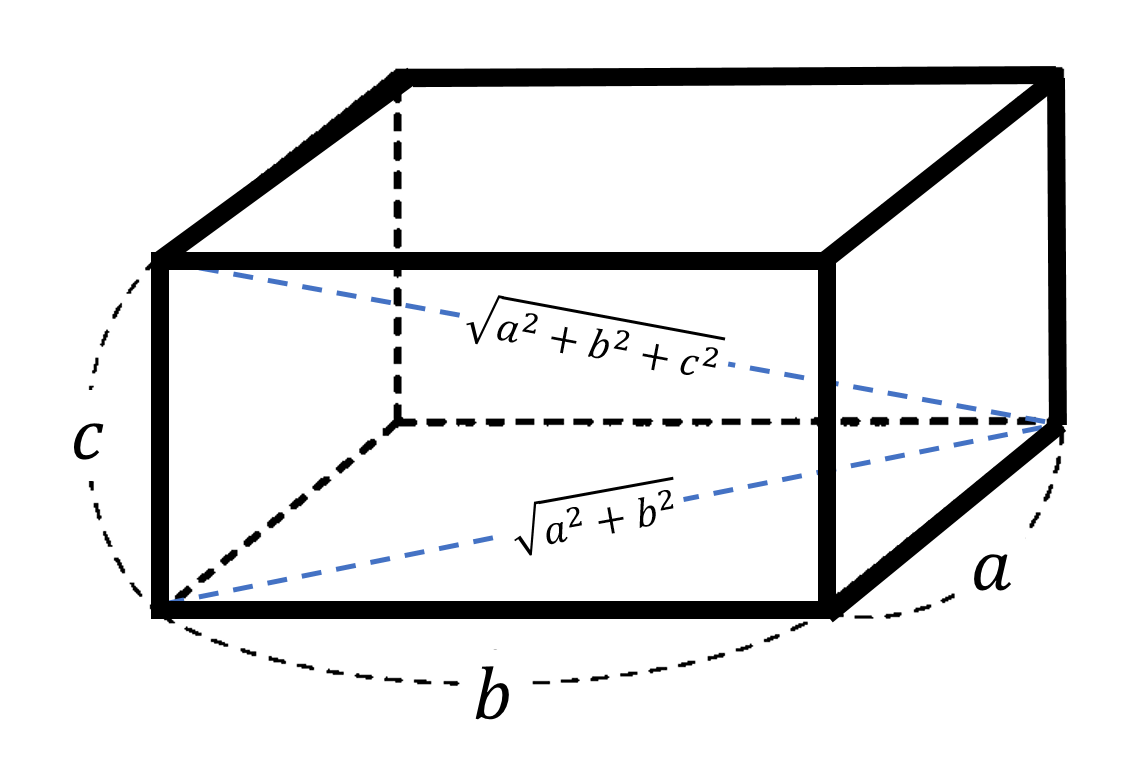
直方体の対角線の長さ:
縦 $a$ 横 $b$ 高さ $c$ の直方体の対角線の長さを $\ell$ とすると $\ell=\sqrt{a^2+b^2+c^2}$
中3 > 8章:標本調査
1年では目的に応じた資料の活用方法について学習し、整理された資料の傾向を読み取ることができるようになりました。しかしながら、実際には、十分な調査をしたくても資料の一部しか得られない場合が多くあります。本章では、このような、資料の一部を上手く用いることで、資料全体の傾向を知る方法について学びましょう。
母集団と標本
資料の一部しか得られない場合、たとえば視聴率調査のような場合において、全国民の視聴傾向をつかむには、どのように調査を行えばよいでしょうか。国民全体のテレビの視聴状況を調査するのは非現実的です。そこで視聴率調査では、全世帯ではなく、一部の世帯を取り出して調査し、その結果から全世帯の視聴傾向を推測しています。このような、対象となる集団全部ではなく一部分を調べて、全体の傾向を推測調査を標本調査といいます。一方で、国勢調査のような、国民全体について調査を行う方法、つまり調査対象となっている集団全部について調査することを全数調査といいます。全数調査を行うと多くの時間や費用がかかる場合や、食品や製品の品質調査などで、調査によって品を駄目にする恐れがある場合には標本調査が行われます。標本調査を行うときに、傾向を知りたい集団全体を母集団、母集団の一部分を取り出して実際に調べたものを標本、取り出した資料の個数を標本の大きさといいます。標本調査は全数調査より精度は劣りますが、偏りがないように上手く標本を取り出すことで、その標本を調べることによって、母集団のおおよその傾向を推定することができ、非常に役に立つ調査方法です。偏りなく標本を抽出することを無作為に抽出する(無作為抽出)といいます。標本調査では、母集団の傾向を上手く推定するために、標本を無作為に抽出する必要があります。標本を無作為に抽出する方法としては、乱数表やコンピュータを用いた方法などがあります。以上、様々な必要な知識を説明しましたが、実際に演習に取り組み、標本調査を利用して母集団全体の傾向や数量などの推定ができるようになりましょう。人間の脳は統計に弱く、それを補うために本章で説明したような統計学を学び身に付けることは、生涯役立つ大きな力となることは間違いありません。
全数調査と標本調査:母集団の全てをとって調べる全数調査と標本を選んで調べ母集団を推定する標本調査とがある。
標本平均と母集団の平均:標本の平均から母集団での平均を推定する。
<参考文献>
[3] “チャート式基礎からの中学3年数学―新学習指導要領準拠”, チャート研究所 数研出版 (2016).
終わりに
以上で中学3年間の数学の概要を全て理解したことになります。各項目の説明を読んで出題されるであろう問題を想像できる程度にまで理解していれば、高校受験でも十分に対応できることでしょう。何度も読み直して「知識の穴」がないよう、しっかりと繰り返し復習しましょう。本記事が一人でも多くの学生の学習の助けになれば幸いです。
※ 以下ここまでに紹介しきれなかった数学が面白くなる動画を紹介します。
数学が面白くなる動画―18
世界は数学で出来ていたのでしょうか?それとも数学は人間が世界を理解するために創り出した便利な道具の一つなのでしょうか?
(1) 数学は神が創った?人が創った?
数学が面白くなる動画―19
恋愛を数学する。マッチングアプリの仕組みとは。
(2) コンピュータが恋愛を理解する?数学を使えばそれも可能に。


