🔄 最終更新日 2020年7月13日 by takara_semi
本記事では中学数学2年で学習するすべての項目について、その概要を確認します。中2数学ではどのような知識を身に付け、どのような計算ができるようになったのでしょうか。これからの人は楽しみに、すでに学んだ人は思い出しながら、一つ一つの項目を確認していきましょう。中2 > 1章:式の計算
中学1年では「1つの文字」にるいての式の計算について学びました。本章では「いくつかの文字」をふくむ式の計算について学びます。扱える文字が増える分、これまでより様々な問題を解決できるようになり、数学の持つ力を垣間見ることができることでしょう。また文字を用いた式を使って「数の性質」を説明する方法についても考えてみましょう。
式の加法・減法
本節では、いくつかの文字をふくむ式の加法と減法の計算について考えます。項の数や文字の個数に着目して考えてみましょう。たとえば $5$ や $3a$ や $xy$ や $\frac{2}{5}b^3$ などのように、文字や数の乗法だけでつくられた式を単項式といいます(1つの文字、1つの数の場合も単項式と考えます)。また $x+4$ や $a-b$ や $3-5x+x^2$ などのように、単項式の和の形をした式を多項式といい、その一つ一つの単項式を、多項式の項といいます(多項式 $a-b$ の場合は $a$, $-b$ が項)。そして、単項式でかけられている文字の個数を次数といいます(たとえば $xy$ の次数は $2$ )。次数が1の式を1次式、次数が2の式を2次式、次数が $n$ の式を $n$ 次式といいます。多項式の次数は、次数の最も大きい項の次数になります(多項式 $x^4-3x^2-5$ の次数は $4$ で、この多項式は「4次式」となる)。用語の説明から具体的な計算方法の説明に移ります。多項式の加法や減法では、文字の部分が同じである項(同類項)をまとめることで計算します。たとえば $3x-7y+2x+9y$ という多項式の計算では、同類項でまとめて $3x+2x$ と $-7y+9y$ とでそれぞれ計算することで結果を得ることができます。1年で学んだ分配法則などを思い出して、効率よく、正確に計算できるように練習しましょう。
括弧をはずす:
(1) $+( )$ なら $( )$ 内の各項の符号は変わらない。分配法則を思い出して利用する。
例
\begin{eqnarray}
& & 3(2x-3y) \\
&=& 3 \times 2x + 3 \times (-3y) \\
&=& 6x-9y
\end{eqnarray}
(2) $―( )$ なら $( )$ 内の各項の符号が変わる。
例
\begin{eqnarray}
& & -3(2x-3y) \\
&=& (-3) \times 2x + (-3) \times (-3y) \\
&=& -6x+9y
\end{eqnarray}
多項式の加法・減法:次の手順で計算する
(1) 括弧をはずす。
(2) 同類項をまとめる。
項を並べかえる $\to$ 同類項を集める $\to$ 係数の計算
例1
\begin{eqnarray}
& & (x^2-3x)-(2x^2-2x-3) \\
&=& x^2-2x^2-3x+2x+3 \\
&=& -x^2-x+3
\end{eqnarray}
例2
\begin{eqnarray}
& & \frac{3x-y}{2}-\frac{2x+3y}{3} \\
&=& \frac{3(3x-y)}{6}-\frac{2(2x+3y)}{6} \\
&=& \frac{3(3x-y)-2(2x+3y)}{6} \\
&=& \frac{9x-3y-4x-6y}{6} \\
&=& \frac{5x-9y}{6}
\end{eqnarray}
単項式の乗法と除法
本節では単項式の乗法と除法の計算方法について考えましょう。除法は逆数を利用して乗法に直して計算する方法に慣れておくと、複雑な計算式でも正確に計算しやすくなります。
(単項式) $\times$ (単項式):係数どうしの積に文字どうしの積をかける。
例
\begin{eqnarray}
& & -3b^3 \times (-3a^2b) \\
&=& (-3) \times (-3) \times b^3 \times a^2b \\
&=& 9a^2b^4
\end{eqnarray}
(単項式) $\div$ (単項式):係数の商を係数に文字の商を文字にかける。逆数を使って積の式になおすと間違いが減り計算しやすくなる。
例
\begin{eqnarray}
& & 5a^3 \div \frac{1}{3}a^2 \\
&=& 5a^3 \times \frac{3}{a^2} \\
&=& \frac{5a^3 \times 3}{a^2} \\
&=& 15a
\end{eqnarray}
式の値:式を計算して簡単にしてから代入する(その方が計算が楽になることが多い)。
例
$a=2,b=-\frac{1}{3}$ のとき $6a^3b^4 \div 2a^2 \div 3ab^2$ の値 $\to$ $6a^3b^4 \div 2a^2 \div 3ab^2$$=b^2=\left(-\frac{1}{3}\right)^2=\frac{1}{9}$ と求まる。
文字式の利用
本節では、複数の文字をふくむ式を使って、いろいろなことがらを説明し、問題を解決してみましょう。たとえば「2つの奇数の和は偶数になる」ことを説明することを考えます。$m,n$ を整数とすると2つの奇数は $2m+1, 2n+1$ として表すことができます。これらの和は $(2m+1)+(2n+1)$$=2m+2n+2$$=2(m+n+1)$ となり $m+n+1$ が整数であるから、2つの奇数の和は偶数になるといえます。このように、文字式を使えば、さまざまなことがらを説明することができるようになります。いろいろな問題に触れて、文字式を使った説明を習得しましょう(このような問は「数学オリンピック」や「数学検定」などにも頻繁に出題される奥が深い問題です。興味のある学生は、図書館などで、これらに関する本を読んでみることをお勧めします)。
整数の表し方:$n$ は整数とする。
(1) 偶数 $\to$ $2n$ 等で表現。
(2) 奇数 $\to$ $2n-1$ または $2n+1$ 等で表現。
(3) 連続する3つの整数 $\to$ $n,n+1,n+2$ または $n-1,n,n+1$ 等で表現。
(4) 連続する3つの奇数 $\to$ $2n-1,2n+1,2n+3$ 等で表現。
※ 「2つの奇数・2つの偶数」などのように「連続する」という指定がない場合は、それぞれ異なる文字を使って表現する。2つの奇数の場合は $m,n$ を整数として $2m+1, 2n+1$ とすることで「2つの奇数」を表現できる。
(5) 3の倍数 $\to$ $3n$ 等で表現。
(6) 3で割って1余る数 $\to$ $3n+1$ 等で表現。
(7) 3で割って2余る数 $\to$ $3n+2$ 等で表現。
等式の変形:目的に応じて式を変形する。等式を変形してある文字について解く。
例
$V=\frac{1}{3}a^2h$ という四角錐の体積を求める式を、高さ $h$ について解く。
\begin{eqnarray}
V &=& \frac{1}{3}a^2h \\
V \times 3 &=& \frac{1}{3}a^2h \times 3 \\
3V \times \frac{1}{a^2} &=& a^2h \times \frac{1}{a^2} \\
\frac{3V}{a^2} &=& h \\
h &=& \frac{3V}{a^2}
\end{eqnarray}
中2 > 2章:連立方程式
中学1年では1つの文字の方程式を解けるようになりました。本章では、2つの文字をふくむ方程式について、その解き方や、その方程式を利用した問題解決の方法について学びましょう。扱える文字が1つ増えるだけで、解ける問題の幅は格段に広がります。連立方程式を、まるでパズルや暗号を解くかのように、楽しみながら解いていきましょう。
連立方程式
本節では2つの文字をふくむ方程式について考えてみましょう。例えば $x+y=5$ のような2つの文字をふくむ1次方程式を2元1次方程式といいます。1年で解けるようになった $x+3=9$ のような式は、詳しくは1元1次方程式(ふつうは単に1次方程式)といいます。また、2元1次方程式を成り立たせる文字の値の組を、2元1次方程式の解といいます。先の例 $x+y=5$ では例えば $x=1, y=4$ や $x=-\frac{1}{2}, y=\frac{11}{2}$ 等の値の組が解となります。さらに2つ以上の方程式を組み合わせたものを連立方程式といいます。例えば
\begin{cases}
{}
x + y = 5 \ ―①& \\
2x + 3y = 12 \ ―②&
\end{cases}
のようなものを連立方程式という。また、組み合わせたすべての方程式を成り立たせる文字の値の組を、連立方程式の解といい、解を求めることを連立方程式を解くといいます。先ほどの例では $x=3, y=2$ がすべての式①②を満たす解だといえます($x,y$ の値の組を2つの式に代入してどちらも成り立つかどうかを調べれば解かどうかを確かめることができます)。連立方程式を解く方法は大きく2つあります。1つ目は加減法です。文字 $x,y$ をふくむ2つの方程式から、そのどちらかをふくまない1つの方程式をつくることを、変数を消去するといいます。どちらかの文字の係数の絶対値をそろえ、左辺どうし、右辺どうしを加えたり引いたりすることで、その文字を消去して解く方法を「加減法」といいます。片方の文字が消去された、1つの文字のみをふくむ方程式であれば、1年に習得した1次方程式の計算方法で解を求めることができます(加減法の詳しい計算方法は以下要点中の計算例を確認してください)。2つ目は代入法です。与えられた2つの式のうちの一方の式を、他方の式に代入することによって文字を消去して解く方法を「代入法」といいます(代入法の詳しい計算方法も以下要点中の計算例を確認してください)。このように、連立方程式の解き方には加減法と代入法の2つがありますが、どちらも「1つの文字を消去して解く」ということに変わりはなく、与えられた連立方程式の形に応じて、計算が楽になりそうな解法を自由に選んで解けばいいのです(問題に指定がなければですが)。「連立方程式を解ける」という力は、数学だけでなく物理や化学など、様々な学問領域を理解するための強力な武器になります。練習問題を解いて、確かな力として着実に身に着けていきましょう。
連立方程式の解き方:次の手順で解く。
(1) まず文字を消去して1つの文字だけの方程式を導く。$\to$ 加減法・代入法
(2) 得られた方程式を解いて1つの文字の値を求める。
(3) もう一方の文字の値を求める。
例1)次の連立方程式を解く(加減法)。
\begin{cases}
{}
2x + 4y = 10 \ ―①& \\
x + 3y = 6 \ ―②&
\end{cases}
$② \times 2$より
\begin{cases}
{}
2x + 4y = 10 \ ―①& \\
2x + 6y = 12 \ ―②’&
\end{cases}
$①-②’$ を計算する
\begin{eqnarray}
2x+4y &=& 10 \\
-) \ 2x+6y &=& 12 \\
\hline\\
-2y &=& -2\\
y &=& 1\\
\end{eqnarray}
この結果を $②$ に代入すると $x=3$ が得られる。よって解は $x=3, y=1$
例2)次の連立方程式を解く(代入法)。
\begin{cases}
{}
2x + 4y = 10 \ ―①& \\
x + 3y = 6 \ ―②&
\end{cases}
$②$より
\begin{equation}
x=6-3y \ ―②’
\end{equation}
$②’$を$①$に代入すると
\begin{eqnarray}
2(6-3y)+4y &=& 10 \\
-2y &=& -2 \\
y &=& 1
\end{eqnarray}
この結果を $②$ に代入すると $x=3$ が得られる。よって解は $x=3, y=1$
いろいろな連立方程式:
例1)分数や小数をふくむ連立方程式:
\begin{cases}
{}
0.1x + y = 0.2 \ ―①& \\
\frac{x+5y}{3} = \frac{1}{2} \ ―②&
\end{cases}
係数が全て整数になるよう変形する。$① \times 10$, $② \times 6$より
\begin{cases}
{}
x + 10y = 2 \ ―①’& \\
2x + 10y = 3 \ ―②’&
\end{cases}
$①’-②’$ を計算する
\begin{eqnarray}
x+10y &=& 2 \\
-) \ 2x+10y &=& 3 \\
\hline\\
-x &=& -1\\
x &=& 1\\
\end{eqnarray}
この結果を $①’$ に代入すると $y=\frac{1}{10}$ が得られる。よって解は $x=1, y=\frac{1}{10}$
例2)等式の形で表現された連立方程式:
連立方程式 $2x+y=x+3y=2$ を解く。$2x+y$ も $x+3y$ も $2$ と等しいことから、次のような連立方程式をつくることができる
\begin{cases}
{}
2x + y = 2 \ ―①& \\
x + 3y = 2 \ ―②&
\end{cases}
$②$より
\begin{equation}
x=2-3y \ ―②’
\end{equation}
$②’$を$①$に代入すると
\begin{eqnarray}
2(2-3y)+y &=& 2 \\
-5y &=& -2 \\
y &=& \frac{2}{5}
\end{eqnarray}
この結果を $②$ に代入すると $x=2-3 \times \frac{2}{5}$$=2-\frac{6}{5}$$=\frac{4}{5}$ が得られる。よって解は $x=\frac{4}{5}, y=\frac{2}{5}$
例3)3つの文字をふくむ連立方程式:
文字が増えても、同じように文字を消去して解く。
\begin{cases}
{}
x + y +z = 2 \ ―①& \\
x + 3y +2z = 3 \ ―②& \\
2x – y + z = 0\ ―③&
\end{cases}
$③$より
\begin{equation}
z=y-2x \ ―③’
\end{equation}
$③’$を$①②$に代入すると
\begin{cases}
{}
x + y +(y-2x) = 2 & \\
x + 3y +2(y-2x) = 3 & \\
\end{cases}
計算すると
\begin{cases}
{}
-x + 2y = 2 \ ―①^{\prime}& \\
-3x + 5y = 3 \ ―②^{\prime}& \\
\end{cases}
$①^{\prime}$より
\begin{equation}
x=2y-2 \ ―①^{\prime \prime}
\end{equation}
$①^{\prime \prime}$を$②^{\prime}$に代入すると
\begin{eqnarray}
-3(2y-2) + 5y &=& 3 \\
6-y &=& 3 \\
y &=& 3
\end{eqnarray}
この結果を $①^{\prime \prime}$ に代入すると $x=2 \times 3-2$$=6-2$$=4$ が得られる。さらにこれらの結果を $③’$ に代入すると $z=3-2 \times 4$$=3-8$$=-5$
よって解は $x=4, y=3, z=-5$
連立方程式の利用
本節では、連立方程式を利用した問題解決について考えます。一般的な手順として(1)どの数量を文字を使って表すかを決める $\to$ (2)数量の間の関係を見つけて2つの方程式を作る $\to$ (3)連立方程式をつくり解を求める $\to$ (4)解が問題に適しているか確かめる、の順に考えることで、答えを求めることができます。与えられた問題にあった連立方程式を自分でつくり、その連立方程式を解くことで、さまざまな問題を解決しましょう。
連立方程式の利用:
(1) 連立方程式をつくる。$\to$ 連立方程式を解く。
(2) 問題の解を求める。$\to$ 連立方程式の解が問題に適しているか調べる。
問題の種類による計算方法:
(1) 代金の問題:代金 $=$ 単価 $\times$ 個数 (※買い物や入園料などの身近な合計代金に関する問題で利用)
(2) 利益の問題:売価 $―$ 原価 $=$ 利益
(3) 速さの問題:道のり $=$ 速さ $\times$ 時間(※距離・速度・時間に関する図を描いて式をつくると間違えにくい。また単位をそろえること)
(4) 濃度の問題:食塩水の濃度(%) $=$ $\frac{食塩の重さ}{食塩水の重さ} \times 100$
(5) 割合の問題:(※生徒数や値段の定価を求める問題などで利用)
$\to$ $b$ は $a$ の $c$ %増 $b=a \times \left( 1+\frac{c}{100} \right)$
$\to$ $d$ は $a$ の $c$ %減 $d=a \times \left( 1-\frac{c}{100} \right)$
(6) 整数の問題:
$\to$ 2桁の自然数 $10a+b$ $(a \neq 0)$
$\to$ 3桁の自然数 $100a+10b+c$ $(a \neq 0)$ ( $a,b,c$ は $0$ から $9$ までの整数)
中2 > 3章:1次関数
中学1年では関数の関係にある2つの数量をみつけて「比例」「反比例」の関係として問題を解決する方法を学びました。本章では、ある2つの数量の「変化の規則性」に注目することで、その関係の特徴を利用した問題解決の方法について学び、1年次より発展的な知識を習得していきましょう。
1次関数とグラフ
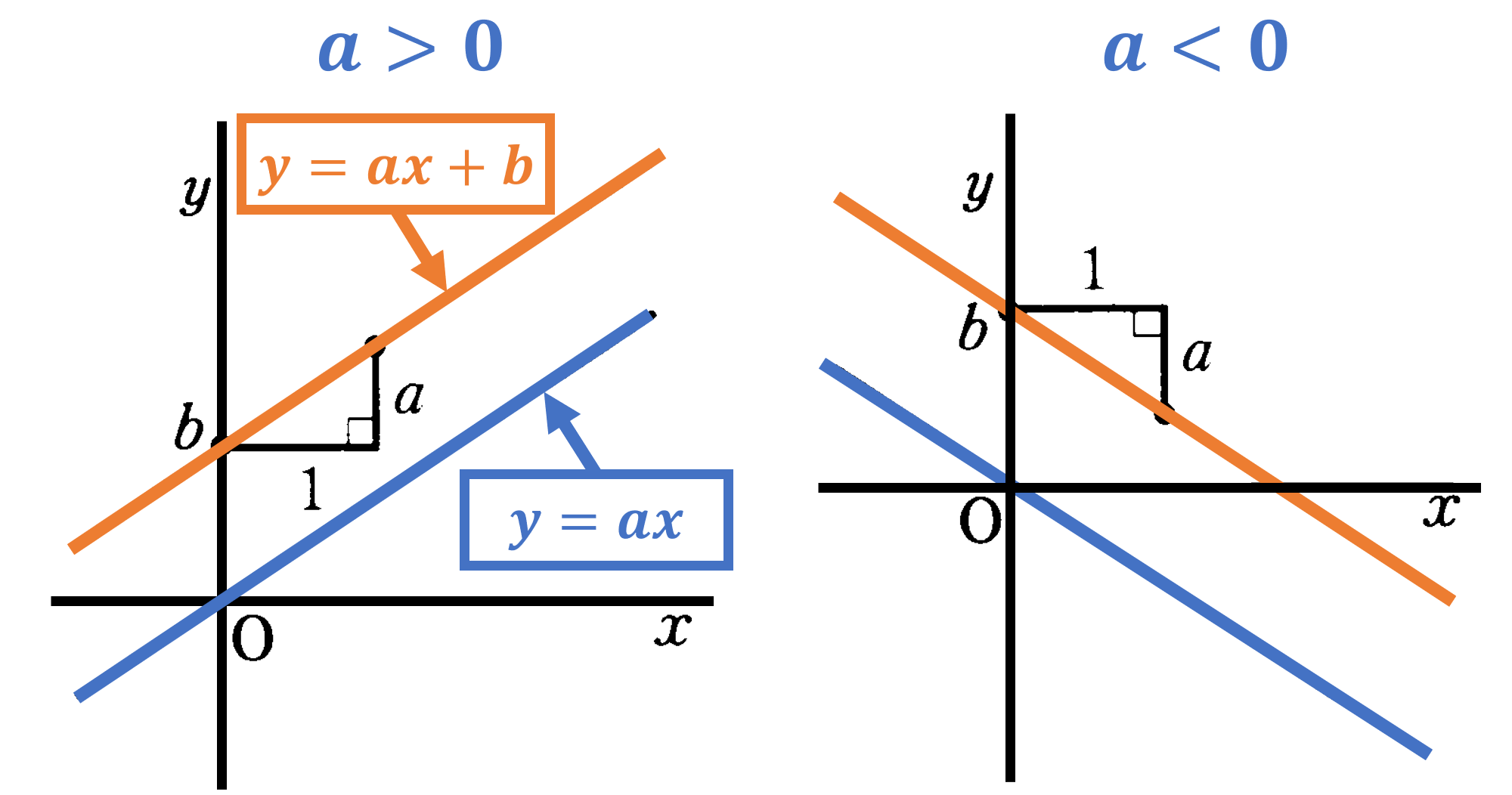
本節では、$y=ax+b$ という式で表される $x$ と $y$ との関係について考えます。2つの変数 $x$, $y$ について、$y$ が $x$ の1次式で表されるとき $y$ は $x$ の1次関数であるといいます。つまり、1次関数は一般に $y=ax+b$ と表されます。1年で学んだ比例の式は $y=ax$ でしたが、これは1次関数の式 $y=ax+b$ の定数 $b$ が $0$ のときの場合です。「比例」は「1次関数の特別な場合」を表していたということです。また $x$ の増加量に対する $y$ の増加量の割合を変化の割合といい、1次関数 $y=ax+b$ では変化の割合は一定で $a$ に等しくなります(※ 変化の割合 $=\frac{yの増加量}{xの増加量}=a$:比例定数 $a$ と変化の割合 $a$ の意味の違いに気を付けること。反比例の関係では変化の割合は一定ではありません。)。つまり、この一定の値 $a$ は、 $x$ の値が $1$ だけ増加した時の $y$ の増加量を表しています。
次に1次関数のグラフの特徴について考えてみましょう。比例のグラフとの関係から考えると、1次関数 $y=ax+b$ のグラフは比例の式 $y=ax$ のグラフを $y$ 軸の正の方向に $b$ だけ平行移動させた直線であると考えることができます。言い換えると、 $y=ax+b$ のグラフは点 $(0,b)$ を通り $y=ax$ のグラフに平行な直線であるともいえます。1次関数 $y=ax+b$ の定数部分 $b$ は $x=0$ のときの $y$ の値でグラフが $y$ 軸と交わる点 $(x,y)=(0,b)$ の $y$ 座標になっています($y=ax+b$ に $x=0$ を代入した時に $y=b$ となることを確認すること)。この $b$ を1次関数のグラフの切片といいます。また変化の割合である $a$ をそのグラフの傾きといいます。つまり1次関数 $y=ax+b$ のグラフは傾きが $a$ 切片が $b$ の直線であるといえます(直線を表す式 $=$ 1次関数であると考えることができます)。傾き $a$ が正の値の場合は $x$ の値が増加すれば $y$ の値も増加する「右肩上がりの直線」 $a$ が負の値の場合は $x$ の値が増加すれば $y$ の値は減少する「右肩下がりの直線」となります。1次関数とそのグラフの関係についてまとめると、変化の割合と傾きが対応し、$x,y$ の値が通る点 $(x,y)$ と対応します。この関係を利用することで、1次関数からグラフを、グラフから1次関数を、それぞれ求めることができます。練習問題に沢山触れることで1次関数の表現になれ、式からグラフをすぐにイメージできるようになりましょう。
1次関数 $y=ax+b$ の値の変化:
(1) 増加・減少: $x$ の値が増加するとき $y$ の値は $a>0$ ならば増加 $a<0$ ならば減少
(2) 変化の割合: 変化の割合 $=\frac{yの増加量}{xの増加量}=a$ (一定)
1次関数 $y=ax+b$ のグラフについて:
(1) 傾き $a$ 切片 $b$ の直線。
(2) 次の2つは等しい:(1) 直線 $y=ax+b$ の傾き $a$ $\iff$ (2) 1次関数 $y=ax+b$ の変化の割合 $a$
(3) $a>0$ のとき右上り(傾き:正) $a<0$ のとき右下り(傾き:負)。
※ 変域を求める方法:1次関数 $y=ax+b$ について $a > 0$ で $x$ の変域が $m < x < n$ のときの $y$ の変域は $am+b < y < an+b$ となる。 $a < 0$ で $x$ の変域が $m < x < n$ のときの $y$ の変域は $an+b < y < am+b$ となる。(グラフから読み取る方法も理解しておくこと)。
1次関数の式の求め方
本節では1次関数の式を求める方法を学びましょう。前節でも説明しましたが、1次関数とそのグラフの関係についてまとめると、変化の割合 $=$ 傾き、$x,y$ の値 $=$ 通る点 $(x,y)$ であるという関係を利用することで、1次関数からグラフを、グラフから1次関数を、それぞれ求めることができます。様々な条件から正しく1次関数の式を求められるよう演習に取り組みましょう。
1次関数の式の決定方法:1次関数 $y=ax+b$ の $a$ と $b$ で決まる。
(1) 通る点と傾きから決定: 傾き $a$ が分かっているため通る点から $b$ を決定する。
例
グラフの傾きが $\frac{2}{3}$ で 点 $(x,y)=(3,1)$ を通る直線の式を求める。傾きが $\frac{2}{3}$ のため求める直線の式は $y=\frac{2}{3}x+b$ である。この式に $(x,y)=(3,1)$ を代入すると $1=2+b \to b=-1$ となる。よって答えは $y=\frac{2}{3}x-1$ となる。
(2) 通る2点から決定:
解法1:2点の座標から傾き $a$ を求めた後に切片 $b$ を決定する。
例
2点 $(-1,2),(3,-4)$ を通る直線の式を求める。グラフの傾きは $a=\frac{2-(-4)}{-1-3}=\frac{6}{-4}=-\frac{3}{2}$ となる。よって求める直線の式は $y=-\frac{3}{2}x+b$ となる。この式に通る点 $(x,y)=(-1,2)$ を代入すると $2=\frac{3}{2}+b \to b=\frac{1}{2}$ となる。よって答えは $y=-\frac{3}{2}x+\frac{1}{2}$ となる。
解法2:2点の座標を $y=ax+b$ に代入し $a$ と $b$ に関する連立方程式を解く。
例
2点 $(-1,2),(3,-4)$ を通る直線の式を求める。2点の座標を $y=ax+b$ に代入すると次の連立方程式が得られる。
\begin{cases}
{}
2 = -a+b \ ―①& \\
-4 = 3a+b \ ―②&
\end{cases}
$①-②$より
\begin{eqnarray}
2-(-4) &=& -a-3a+b-b \\
6 &=& -4a \\
a &=& -\frac{3}{2}
\end{eqnarray}
この結果を$①$に代入すると
\begin{eqnarray}
2 &=& \frac{3}{2}+b \\
b &=& 2-\frac{3}{2} \\
b &=& \frac{1}{2}
\end{eqnarray}
が得られる。よって求める直線の式は$y=-\frac{3}{2}x+\frac{1}{2}$となる。
1次関数と方程式
本節では、2つの文字 $x,y$ をふくむ2元1次方程式 $ax+by=c$ ($a,b,c$ は定数とします)の表すグラフについて考えてみましょう。この方程式を成り立たせる $x,y$ の組は無数に存在し、この $x,y$ の値の座標をグラフとして描くと、直線になります。2元1次方程式 $ax+by=c$ を見やすい形に表すために $y$ について解くと $y=-\frac{a}{b}x+\frac{c}{b}$ となり、傾き $-\frac{a}{b}$ 切片 $\frac{c}{b}$ の直線であることが分かります。この直線を方程式 $ax+by=c$ のグラフといいます。このグラフは方程式 $ax+by=c$ の解を座標にもつ点の集まりでできた直線です。とくに $a=0$ の場合は $x$ 軸に平行な直線( $y=\frac{c}{b}$ )、$b=0$ の場合は $y$ 軸に平行な直線( $x=\frac{c}{a}$ )になります。ここでは説明を一般化するために $a,b,c$ を用いて説明しましたが、そこに具体的な数字を入れて、いろいろな方程式のグラフを描いてみましょう。きっと理解が深まるはずです。
続いて、2つの2元1次方程式(連立方程式)とグラフの関係について考えてみましょう。先ほど1つの2元1次方程式が直線のグラフとなることを学びました。さらに、その直線は、その方程式の解の集まりだということも学びました。これらのことから、2つの2元1次方程式をグラフにしたとき、2本の直線ができ、さらにその2直線の交点 $(p,q)$ は、2つの方程式をそれぞれ成り立たせる解、つまり連立方程式の解となることが分かります。整理すると $x,y$ についての連立方程式の解は、それぞれの方程式のグラフの交点の $x$ 座標 $y$ 座標の組となります。このようにして、グラフを活用して連立方程式を解くことができます。関数のグラフと方程式の関係を正しく理解し、問題に合った解き方ができるようになりましょう。
2元1次方程式 $ax+by=c$ のグラフについて:
(1) 直線を表す。
(2) $a \neq 0$, $b \neq 0$のとき $y$ について解くと $y=px+q$($y=-\frac{1}{b}x+\frac{c}{b}$)の形となる。 $\to$ この1次関数のグラフと一致する。
$x$軸, $y$軸に平行な直線:
(1) $y=q$ のグラフ:$x$軸に平行な直線となる。
(2) $x=p$ のグラフ:$y$軸に平行な直線となる。
$ax+by=c$ について:
$a=0$, $b \neq 0$ のとき: $by=c$ $\to$ $y=\frac{c}{b}$ の直線となる。$\frac{c}{b}=q$とすれば上(1)の例と同じグラフになる。
$a \neq 0$, $b=0$ のとき: $ax=c$ $\to$ $x=\frac{c}{a}$ の直線となる。$\frac{c}{b}=p$とすれば上(2)の例と同じグラフになる。
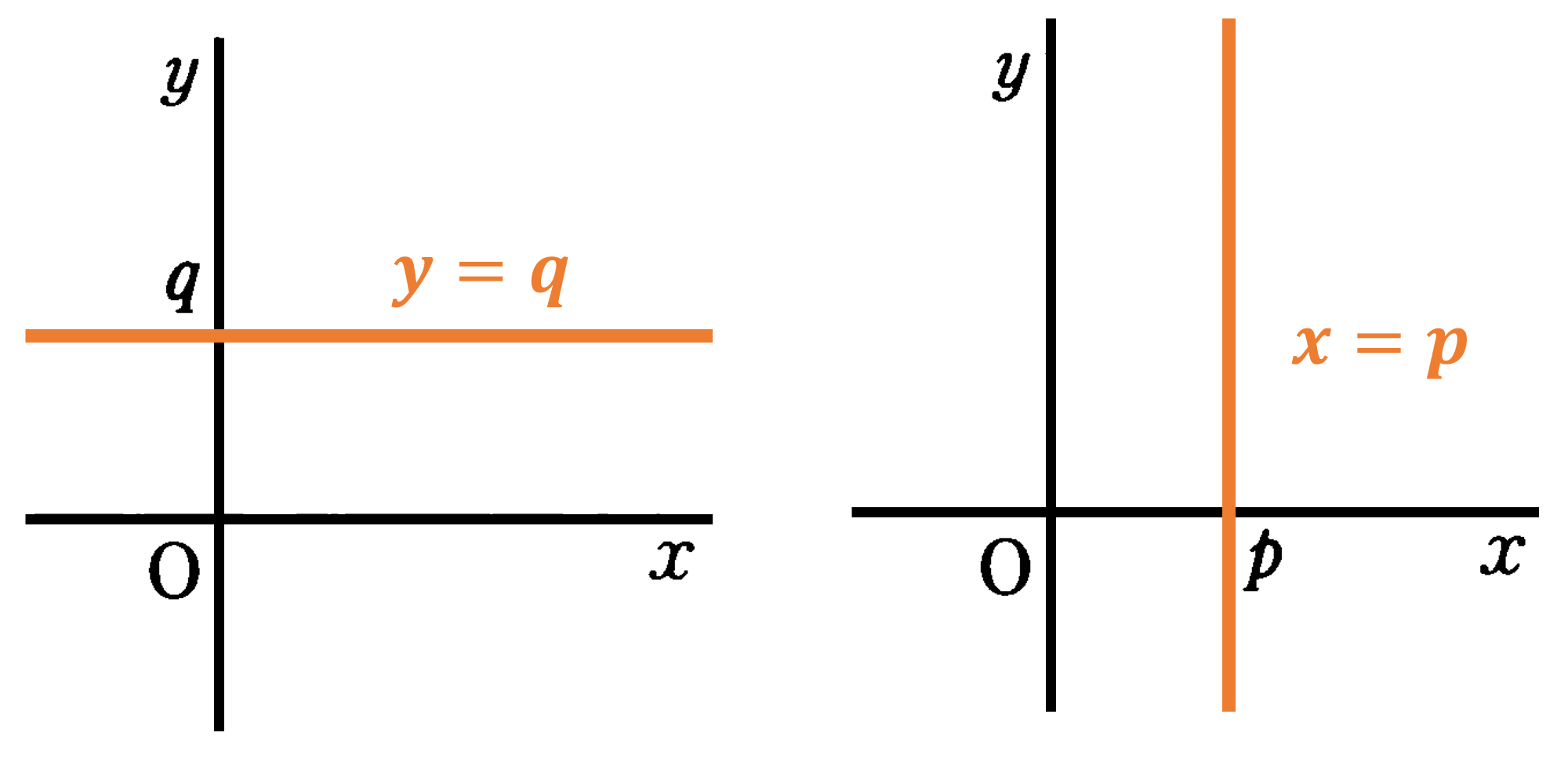
連立方程式とグラフ:
次の2つは等しい:(1) 連立方程式 $
\begin{cases}
{}
ax + by = c & \\
a’x + b’y = c &
\end{cases}
$ の解 $\iff$ (2) 2直線 $
\begin{cases}
{}
ax + by = c & \\
a’x + b’y = c &
\end{cases}
$の交点の座標
1次関数の利用
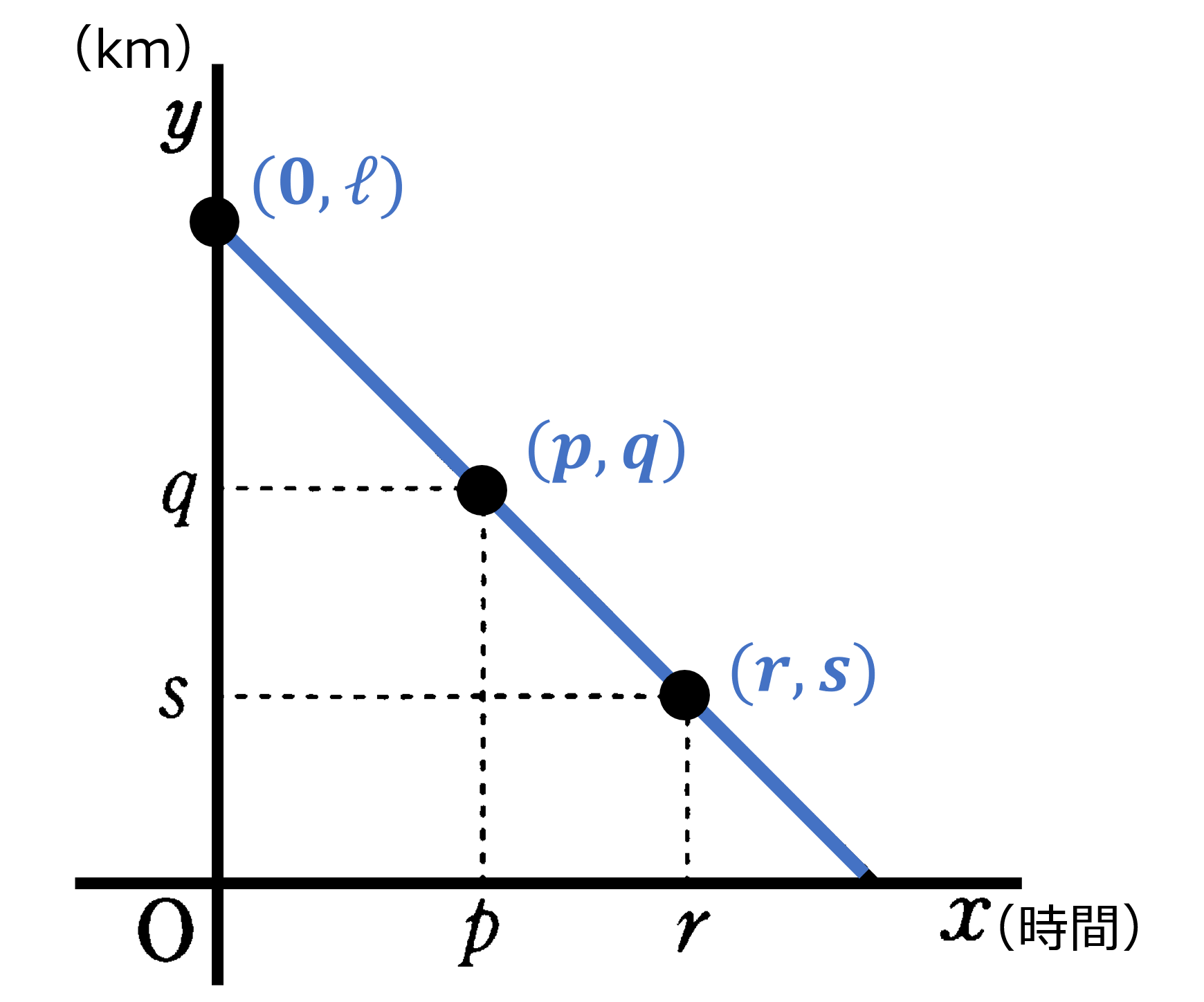
本節では1次関数を利用して問題を解決することを考えます。例えばやかんや水筒の温度の変化を調べたり、標高と気温の関係を考察したり、電車のダイヤグラムを読み取ったり、水道光熱費や携帯料金と使用量と料金の関係を調べたり、図形の面積の変化を考えたりと、ある2つの数量の間の関係を1次関数とみなして解決できる問題は無数にあります。実際に具体的な問題に取り組み、1次関数とそのグラフを活用して、問題を解決してみましょう(図形の面積を1次関数で表現する問題として「点Pが辺上を移動する」という問題はよく出題されます。いくつかのパターンを解いて理解を深めておきましょう)。
一定の速さで動く点の位置をグラフに表す:
例
A君が$\ell$km 離れた出発点からこちら(距離0の地点)に向かって歩いている。A君は $x$ 時間後に出発点から $y$ km の距離にいるとする。このとき次の2つは等しい:
(1) $x=p$ のとき $y=a$, $x=r$ のとき $y=s$ である。$\iff$ (2) 2点 $(p,q)$, $(r,s)$ を通る。
中2 > 4章:図形の性質と合同
本章では簡単な図形の性質から複雑な図形の性質まで、順を追って正しく理解していくことが目的です。図形の性質やその表現を習得することで、ロボット工学やコンピュータグラフィックスなど、あなたの数学の知識を活用できる場がより一層広くなることでしょう。
平行線と角
本節では平行線と角の性質を説明する(導く)ことを考えます。まず2直線が交わってできる角についてみていきます。2つの直線が交わると、その交点の周りに角ができます。それらの角のうち、向かい合っている角を対頂角といい、その性質として「対頂角は等しい」ということがいえます(その理由を説明できるように:$180^{\circ}-$(共通の角) が等しいことから説明可)。続いて2つの直線に1つの直線が交わってできる角について、その位置関係によって同位角と錯角と呼ばれる角があります。錯角は「たがいちがいの角」という意味です。位置関係と角の呼び方、およびその特徴については要点を確認してください。とくに平行線と同位角・錯角の特徴は重要なポイントなので、正しく理解しておきましょう。平行線の性質として、2直線に1つの直線が交わるとき (1) 2直線が平行ならば同位角は等しい (2) 2直線が平行ならば錯角は等しい ということがいえます。またこれらの性質から、2直線が平行線になる条件として (1) 同位角が等しければその2直線は平行である (2) 錯角が等しければその2直線は平行である ということがいえます。
対頂角・同位角・錯角:
(1) 対頂角は等しい
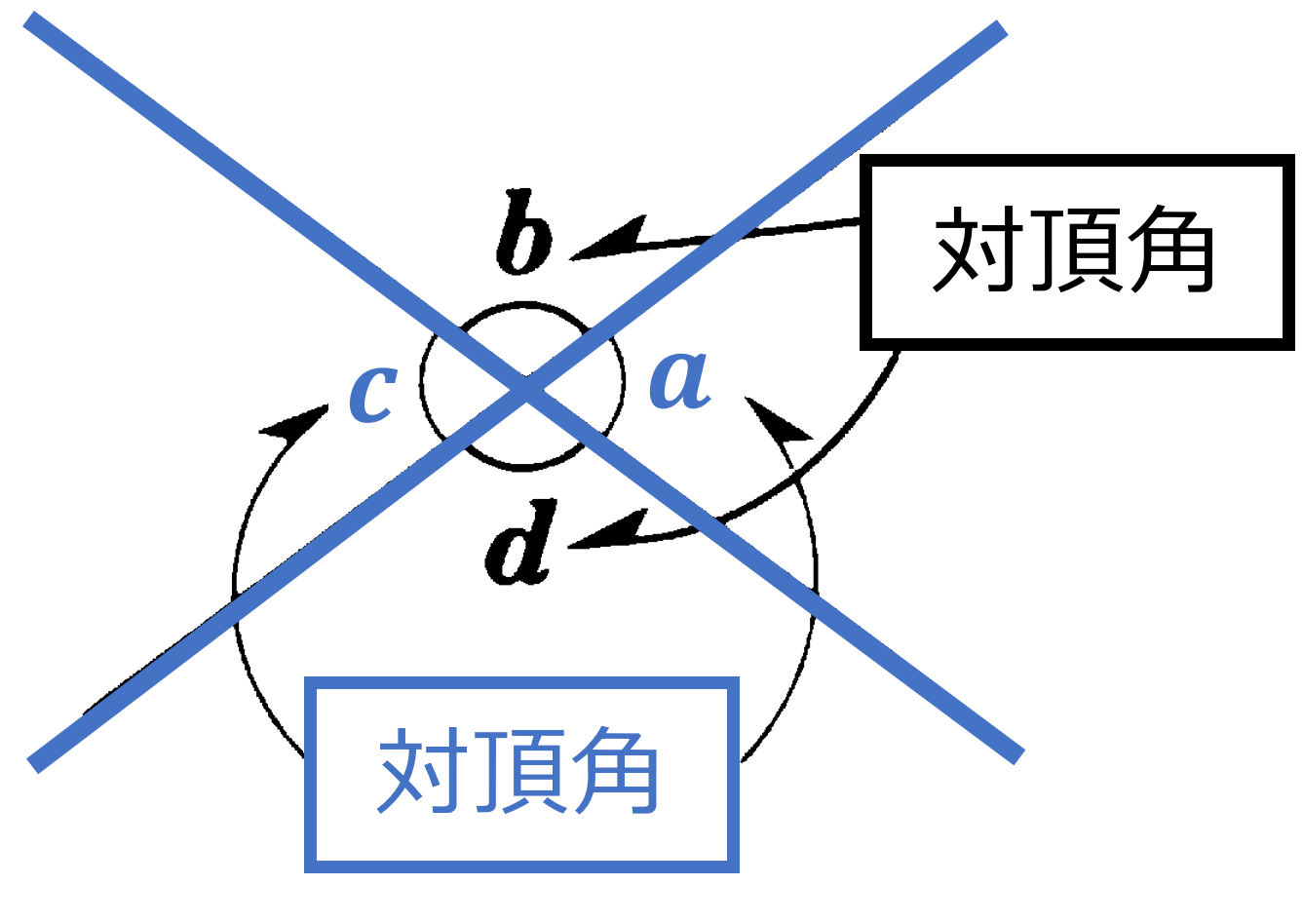
(2) 2直線に1直線が交わってできる角
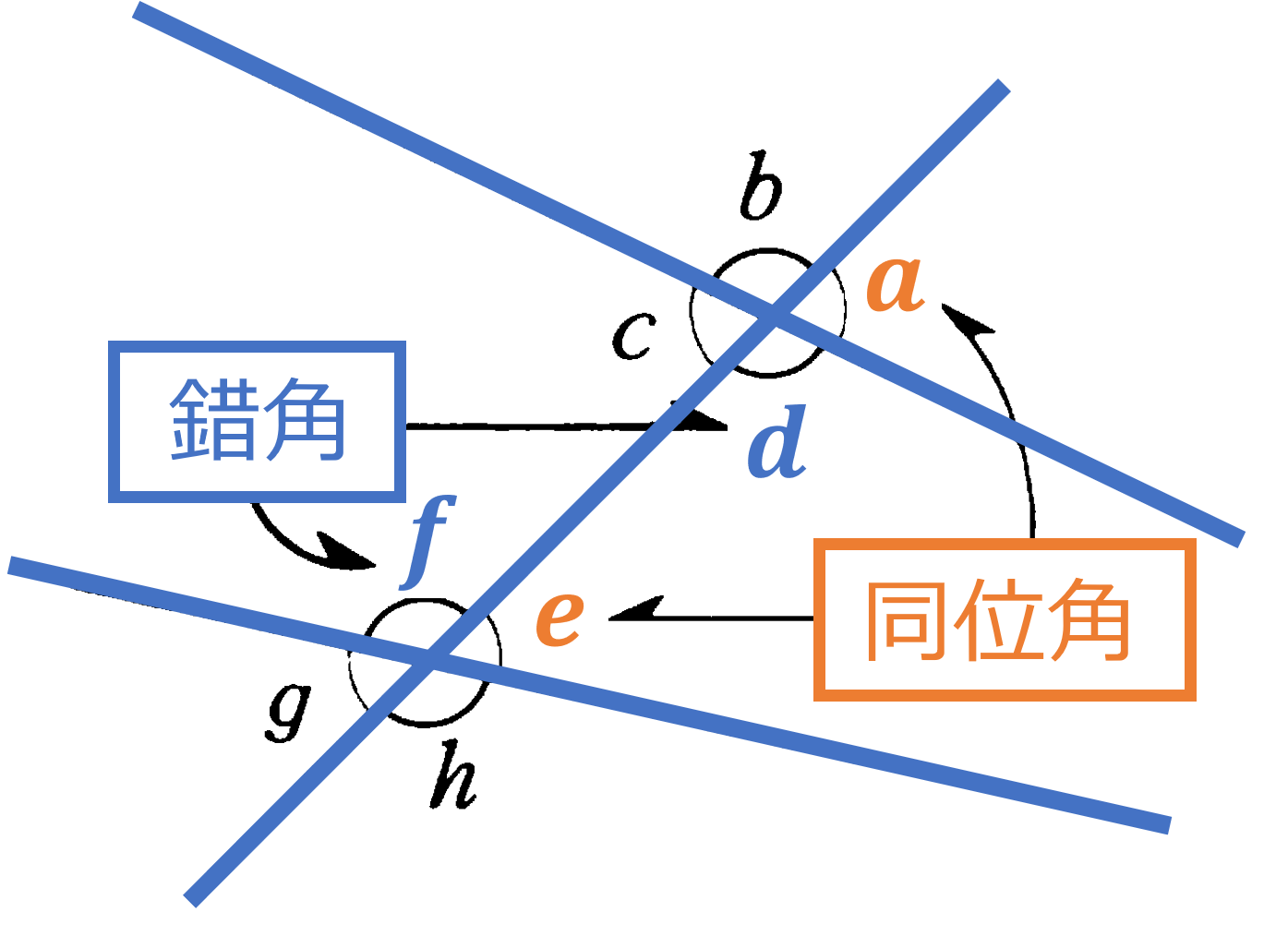
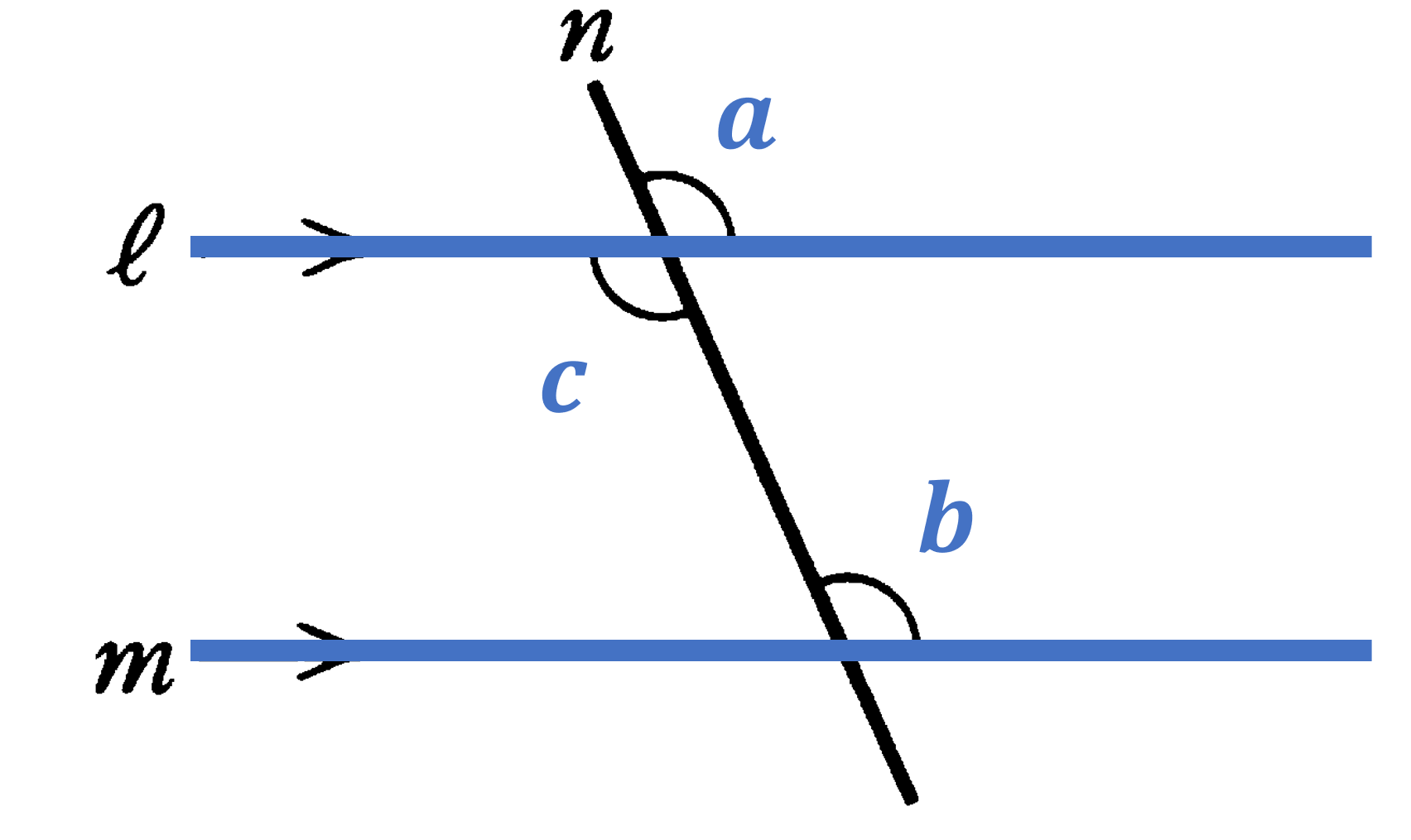
平行線と同位角・錯角:
(1) 平行 $\iff$ 同位角が等しい:$\ell / \! \! / m \iff \angle a=\angle b$
(2) 平行 $\iff$ 錯角が等しい:$\ell / \! \! / m \iff \angle c=\angle b$
多角形の角
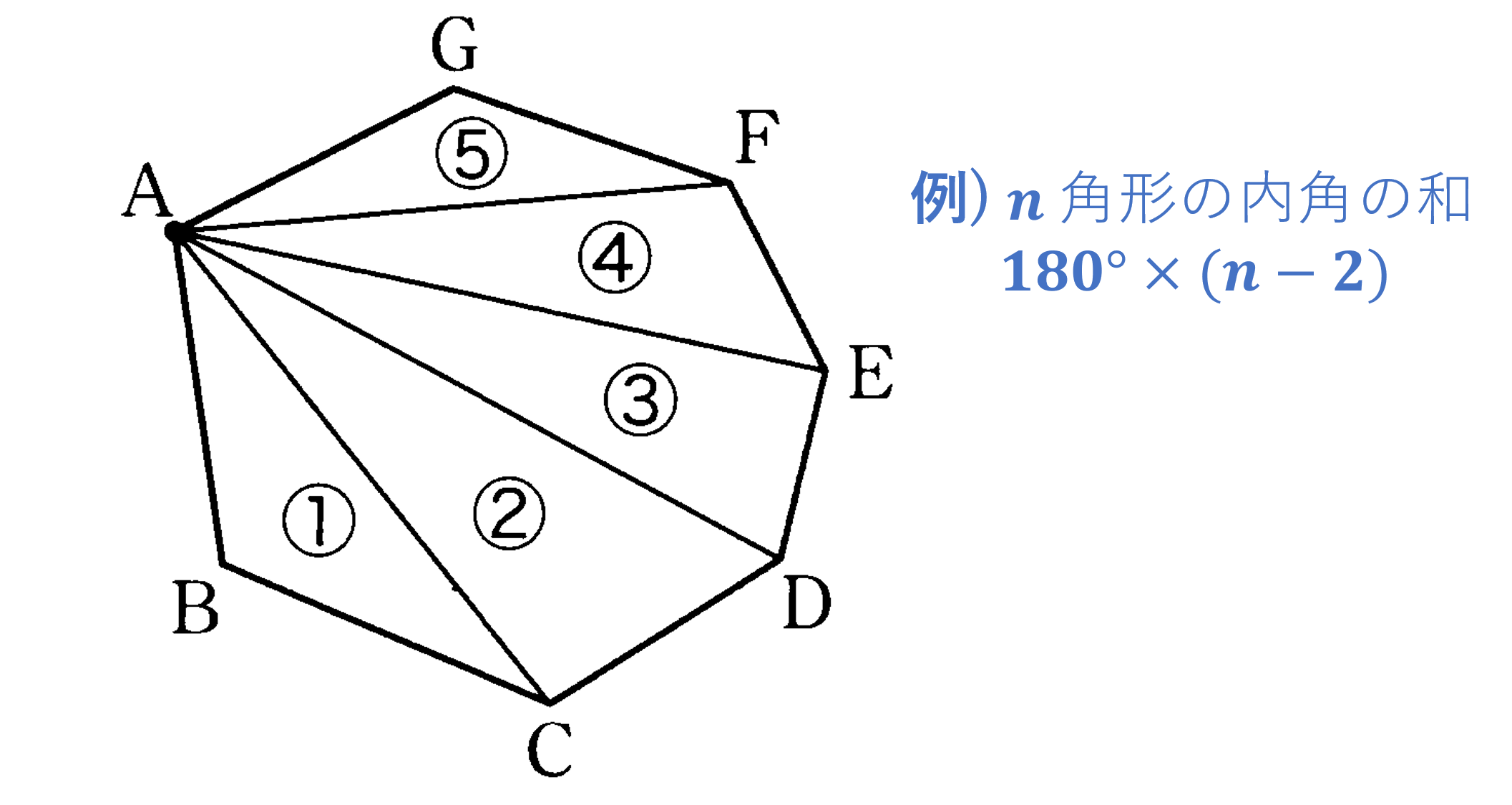
本節では多角形の角について考えてみましょう。ここで多角形というときにはへこんだ部分があるものは考えないものとします。多角形の2辺が作る内側の角を内角、1つの辺と隣りの辺の延長とが作る角を、その頂点の外角といいます。次に、平行線と角の性質を利用して、三角形の内角の和が $180^{\circ}$ であることを説明してみましょう。ある ${\rm \triangle{ABC}}$ の頂点Aを通り、辺BCに平行な直線DEをひきます(説明や計算の理解を助けるためにひく、このような線を補助線といいます)。このとき、次のことが成り立ちます。
(1) 平行線の錯角は等しいから ${\rm \angle ABC}={\rm \angle BAD} \ -①$
(2) 平行線の同位角は等しいから ${\rm \angle BCA}={\rm \angle CAE} \ -②$
したがって ${\rm \triangle{ABC}}$ の内角の和は $①②$ より
${\rm \angle ABC}+{\rm \angle BCA}+{\rm \angle CAB}$$={\rm \angle BAD}+{\rm \angle CAE}+{\rm \angle CAB}$$=180^{\circ}$
となることがいえます。他にも多角形の角の性質は多くありますので、要点でその内容を確認しておきましょう。
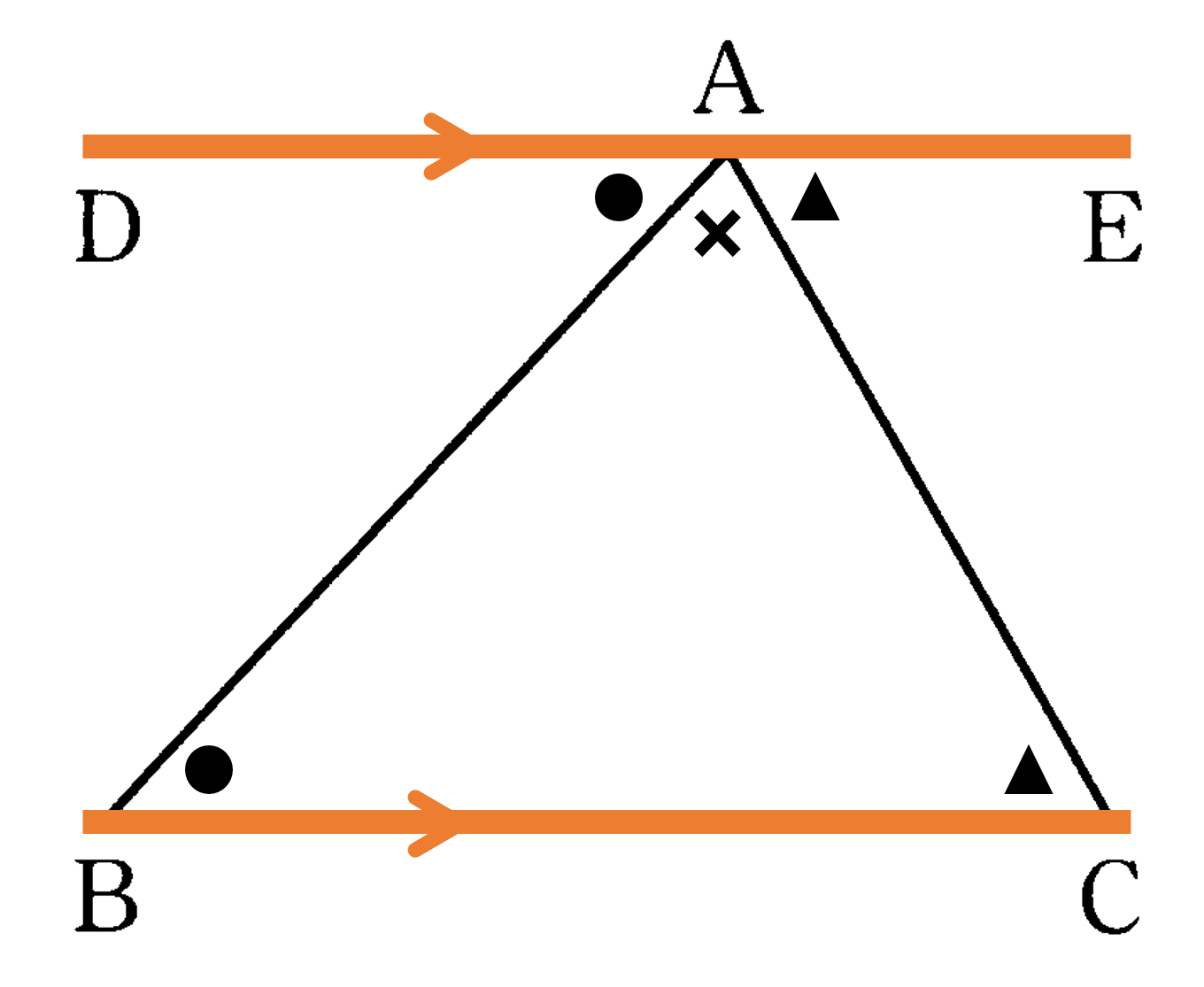
三角形の内角と外角:
(1) 内角の和は $180^{\circ}$
(2) 外角はその隣にない2つの内角の和に等しい。
(3) 外角の和は $360^{\circ}$
多角形の内角と外角:
(1) $n$角形の内角の和 $180^{\circ}×(n-2)$
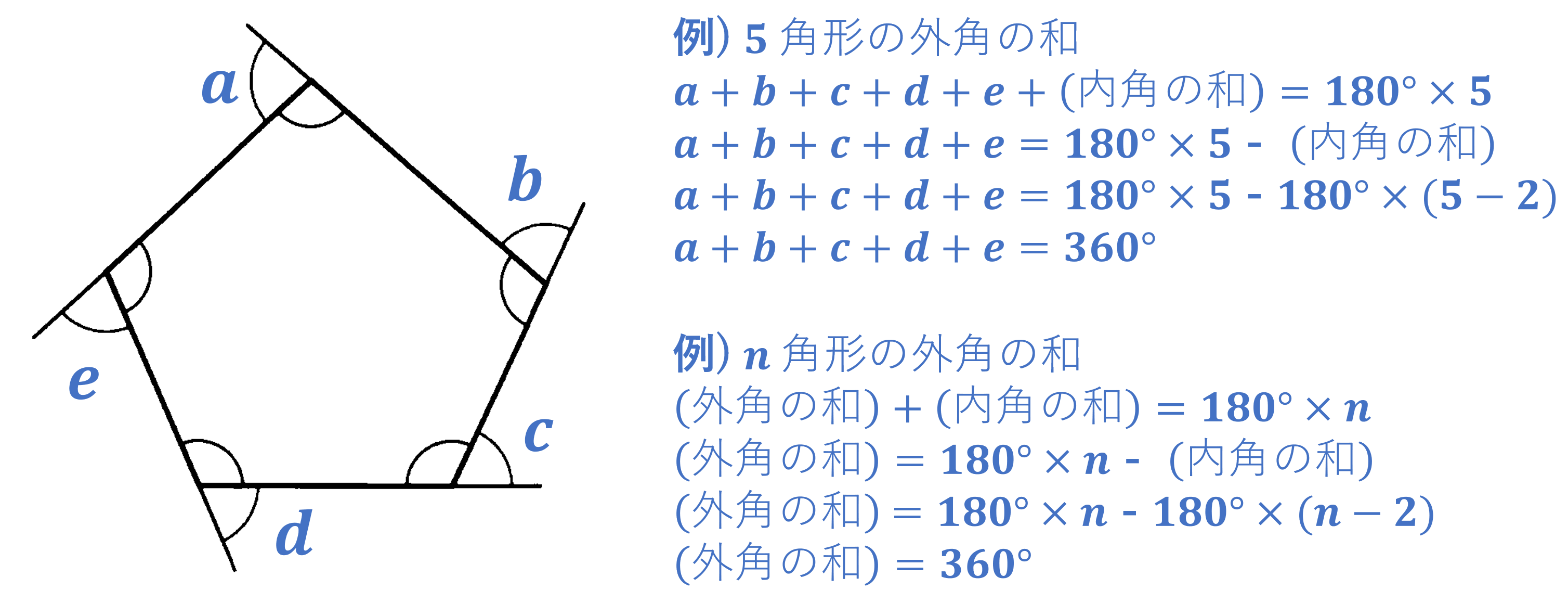
(2) 多角形の外角の和 $360^{\circ}$
三角形の合同
本節では図形の合同について考えてみましょう。平面上の2つの図形について、一方を移動・回転・反転することで他方に重ね合わせることができるとき、この2つの図形は合同であるといいます。そして合同であることを記号 $\equiv$ で表します。例えば 四角形ABCD $\equiv$ 四角形EFGH のようにかき、対応する頂点の名前の順に示します(頂点AとE、頂点BとF…がそれぞれ対応します)。また合同な図形では対応する線分や角は等しくなります。
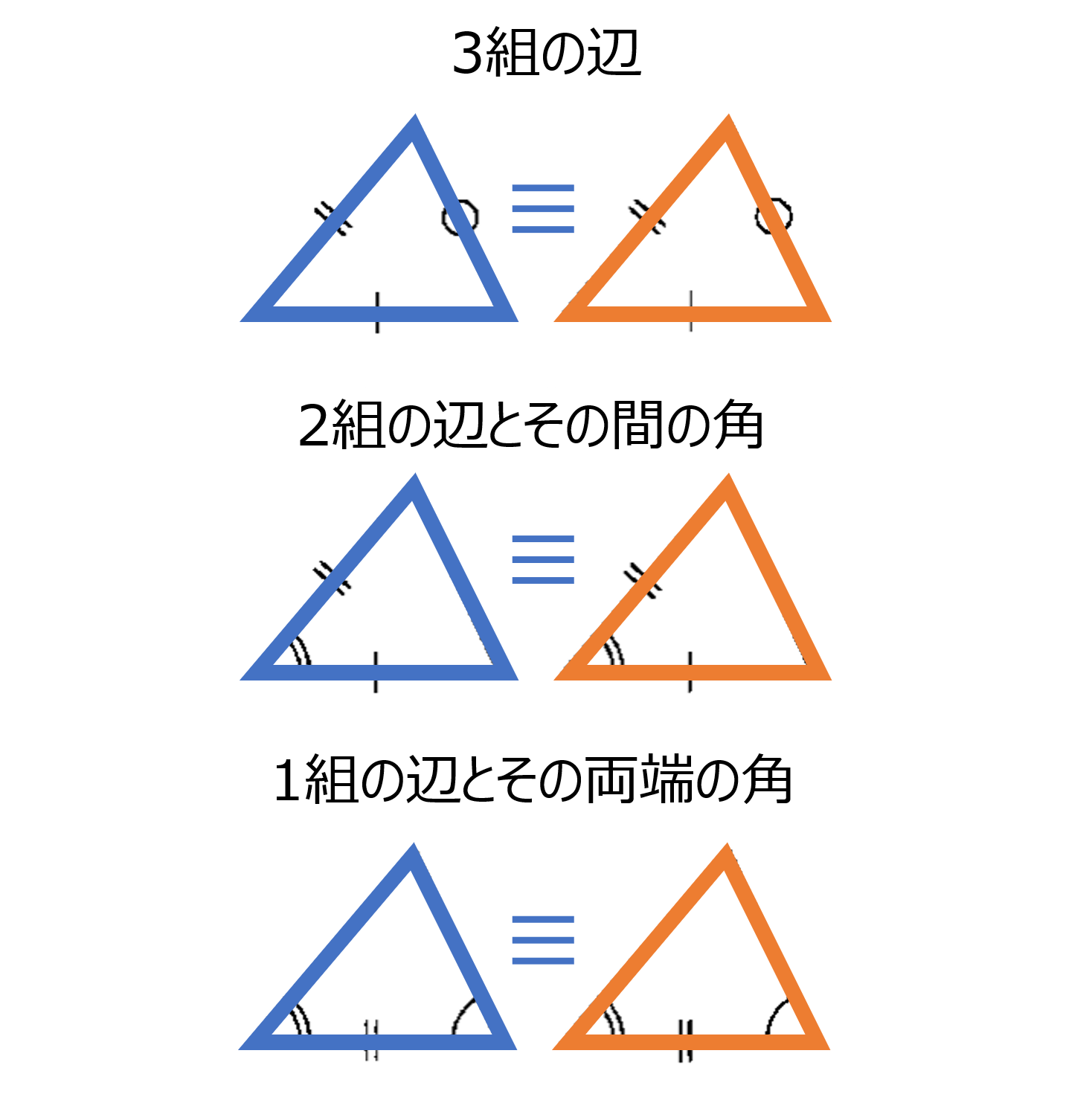
ここからは平面図形の中でも特に三角形の合同について考えていきます。様々な三角形を観察すると、2つの三角形が合同かどうかを判断するには次の合同条件を満たすかどうかを調べればよいことが分かります。(1) 3組の辺がそれぞれ等しい (2) 2組の辺とその間の角がそれぞれ等しい (3) 1組の辺とその両端の角がそれぞれ等しい。2つの三角形の合同を調べるときには、これらの合同条件のいずれかに当てはまれば合同であると判断することができます。この合同条件は文言も含めて正しく覚えて使えるようになりましょう。合同の意味を理解していれば、言葉も自然と暗記できることかと思います。
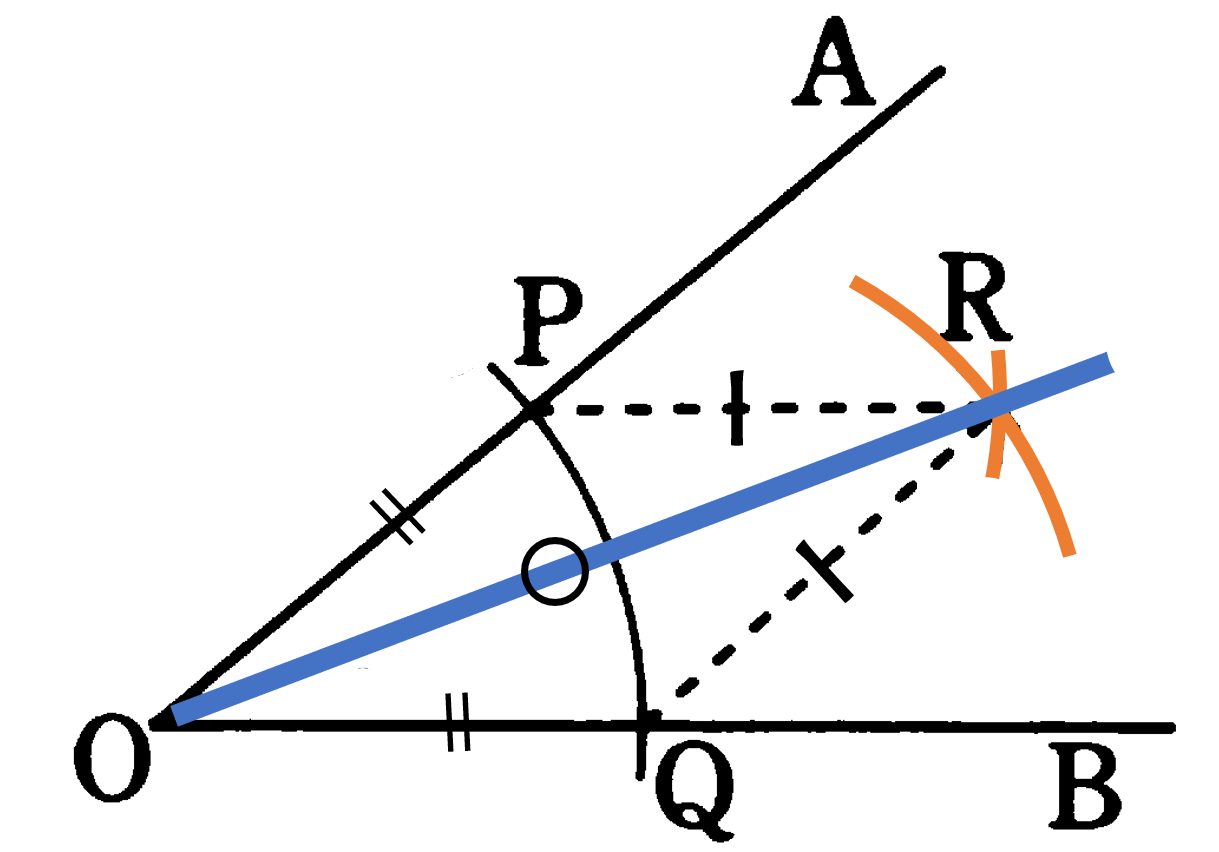
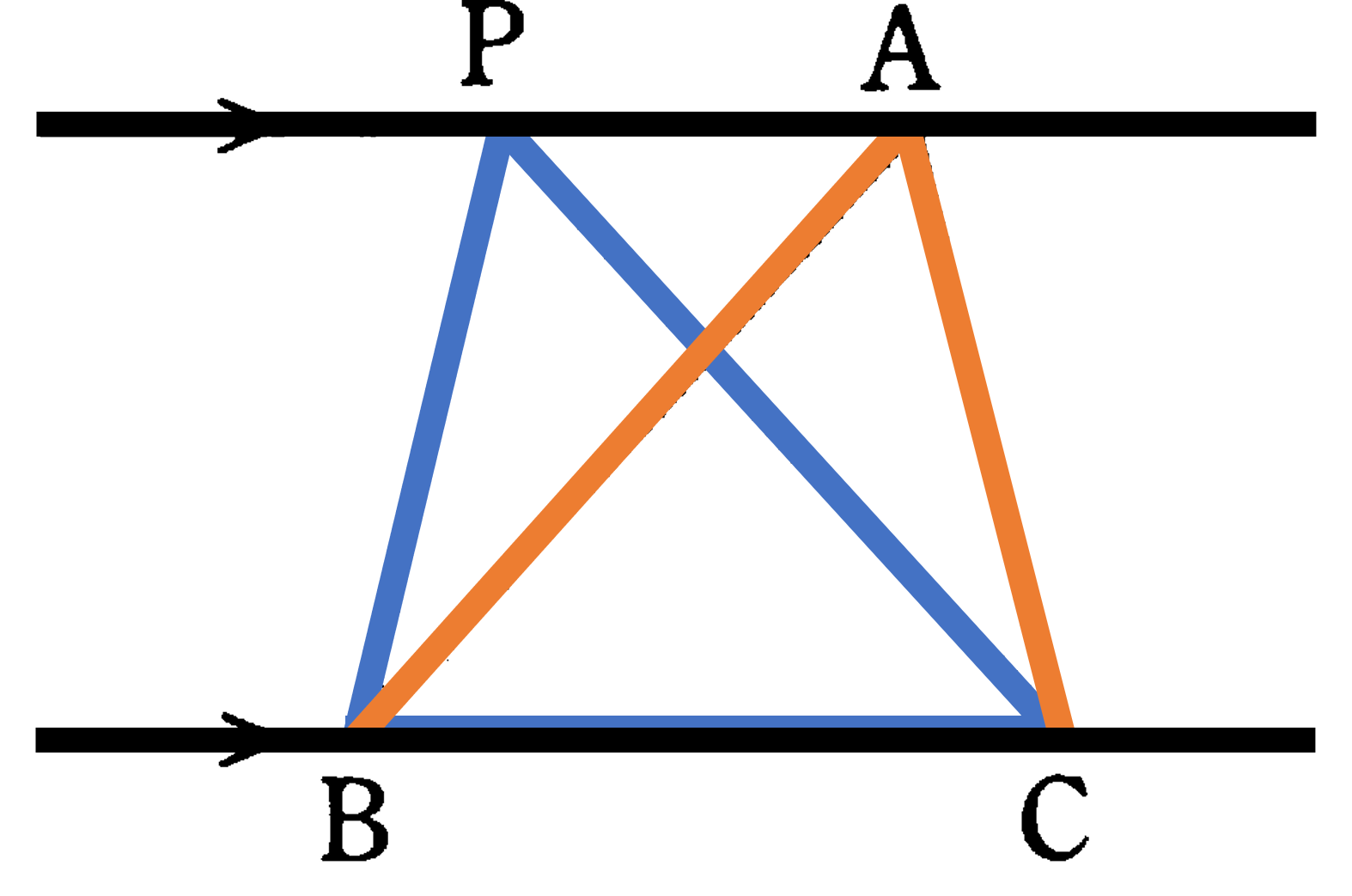
最後に三角形の合同条件を利用した証明について考えてみましょう。三角形の合同条件を利用することで、角の二等分線の作図が正しいことを確かめましょう。
下の図に角の二等分線の作図によって描かれた2つの三角形 ${\rm \triangle{OPR}}$, ${\rm \triangle{OQR}}$ を示します。この図で ${\rm \triangle{OPR}}$, ${\rm \triangle{OQR}}$ において
コンパスを用いた作図であるため
${\rm OP}={\rm OQ} ―①$
${\rm PR}={\rm QR} ―②$
また共通する辺であるため
${\rm RO}={\rm RO} ―③$
よって $①②③$ より 3組の辺がそれぞれ等しいから ${\rm \triangle{OPR}}$$\equiv$${\rm \triangle{OQR}}$ がいえ、合同な図形の対応する角は等しいことから ${\rm \angle ROP}={\rm \angle ROQ}$ となり、ORは ${\rm \angle POQ}$ の二等分線であるといえます(証明終了)。
このような、三角形の合同条件を利用した証明の問題は入試問題としてもよく取り上げられます。角や平行線の性質、等式の性質、面積や体積の公式なども証明の根拠として利用されることがあります。これらも合わせて、正しく理解して着実に身に着けていきましょう。
三角形の合同条件:次の(1)(2)(3)いずれかが成り立てば合同。
(1) 3組の辺 (2) 2組の辺とその間の角 (3) 1組の辺とその両端の角
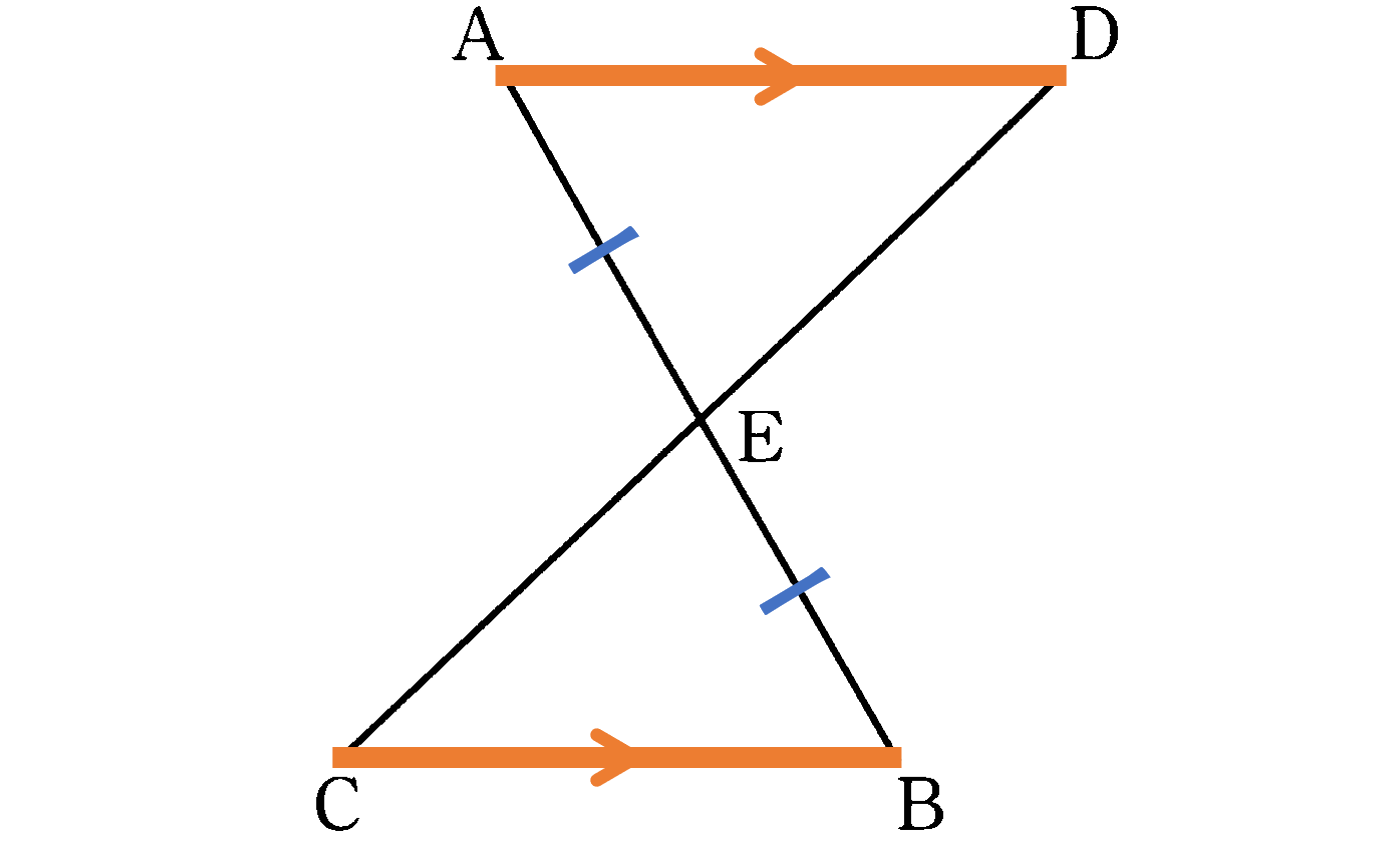
例
下図で ED $=$ EC となることを証明する $\to$ 仮定(条件)から結論(三角形の合同)を導く。
${\rm \triangle{AED}}$ と ${\rm \triangle{BEC}}$ において
仮定から
${\rm EA}={\rm EB} ―①$
対頂角は等しいから
${\rm \angle AED}={\rm \angle BEC} ―②$
平行線の錯角は等しいから
${\rm \angle EAD}={\rm \angle EBC} ―③$
$①②③$ より 1組の辺とその両端の角がそれぞれ等しいから
${\rm \triangle{AED}}$$\equiv$${\rm \triangle{BEC}}$
合同な図形の対応する辺は等しいから
${\rm ED}={\rm EC}$ (証明終了)
証明
この節では「証明」について再確認していきましょう。証明とは、先の節であった「平行線と角の性質を利用して、三角形の内角の和が $180^{\circ}$ であることを説明する」例のように「あることがらが成り立つ理由」を「すでに正しいと分かっている性質を根拠にして示す」ことをいいます。この例では「三角形の内角の和が $180^{\circ}$ になる理由」を「自明な平行線の性質を根拠にして示す」という証明をしたといえます。このように平行線の性質や三角形の性質を利用して証明可能な図形の性質として、次のようなものがあります。「三角形の内角の和は $180^{\circ}$ である」「三角形の外角は、それと隣り合わない2つの内角の和に等しい」「$n$ 角形の内角の和は $180^{\circ} \times (n-2)$ である」「多角形の外角の和は $360^{\circ}$」。平行線の性質 $\to$ 三角形の内角の和 $\to$ 多角形の内角の和 $\to$ 多角形の外角の和 の順で証明できます。証明や図形の問題になれるために、それぞれの性質を自分で証明できるようになっておきましょう。
仮定と結論:ことがら「(ア)ならば(イ)」について考える。
(ア):与えられて分かっていること $\to$ (ア)の部分が仮定
(イ):(ア)から導こうとしていること $\to$ (イ)の部分が結論
数学が面白くなる動画―12
証明を間違えると大変なことになる?証明を積み立てることで数学はどんどん楽しくなる。
中2 > 5章:三角形と四角形
本章では三角形と四角形の性質を調べます。特に線対称な図形である二等辺三角形や、点対称な図形である平行四辺形の性質を詳しく調査し、その性質を証明してみましょう。
三角形
本節では三角形の性質について考えてみましょう。まずは二等辺三角形についてです。二等辺三角形とは「2つの辺が等しい三角形」のことです。このように、言葉の意味をはっきりと述べたものを定義といいます。この定義をもとにして、より発展的な事実を証明していくことで、その性質をより深く知ることができるのです。例えば、二等辺三角形の2つの角は等しいということも、この定義を根拠に、合同条件を利用して証明することができます。また二等辺三角形で、長さの等しい2つの辺の間の角を頂角といい、頂角に対する辺を底辺、底辺の両端の角を底角といいます。「二等辺三角形の底角は等しい」「三角形の内角の和は $180^{\circ}$」「二等辺三角形の頂角の二等分線は底辺を垂直に2等分する」等の性質は、当然の事実として証明の根拠としても利用されますが、定義ではありません。これらは定義などを根拠に証明された性質のひとつであり、このような証明された大切なことがらを定理といいます(高度な数学は、この確かな根拠に裏付けられた「定理」の積み重ねによって成り立っているといっても過言ではありません)。このような定理を利用することで、複雑な問題を簡単に解決することができるようになります。
次に正三角形について考えてみましょう。正三角形とは「3つの辺が等しい三角形」のことです。これが正三角形の定義です。この定義から容易に「正三角形の3つの角は等しい」という定理を証明することができます(二等辺三角形の底角が等しいという定理を利用します)。(※ 三角形は角によって3つに分類することができます。3つの角がすべて鋭角( $0^{\circ}$ より大きく $90^{\circ}$ より小さい角)のものを鋭角三角形、1つの角が直角のものを直角三角形、1つの角が鈍角( $90^{\circ}$ より大きく $180^{\circ}$ より小さい角)のものを鈍角三角形といいます。)
続いて、三角形にどんな条件が加わると二等辺三角形になるかを考えてみます。先に「三角形の2辺が等しいとき、2つの角は等しい」ということを証明しましたが、逆の「2つの角が等しい三角形の2辺は等しい」も成り立つといえるでしょうか。これは図形の合同を利用することで証明可能です。つまり二等辺三角形になるための条件の定理として「三角形の2つの角が等しければ、その三角形は、等しい2つの角を底角とする二等辺三角形である」ということがいえます。同様に、正三角形になる条件の定理として「3つの角が等しい三角形は正三角形である」ということもいえます。ここで、定理の逆というものについて考えてみましょう。「三角形の2つの辺が等しい時、2つの角は等しい…①」ことと「三角形の2つの角が等しいとき、2つの辺は等しい…②」ことは、定理の仮定と結論を入れかえたものであり、このようなものを定理の逆といいます。すなわち②は①の逆であり、①は②の逆です。また「正しいことの逆」がいるも正しいとは限りません。例えば「 $x≧7$ ならば $x > 5$ 」ということがらは正しいですが、逆の「 $x > 5$ ならば $x≧7$ 」ということがらは $x=6$ では成り立たず、正しいといえません。このような、あることがらが成り立たない例を反例といい、あることがらが正しくないことを示すには反例を1つあげればよいといえます。このように、ある定理の逆が正しいということをいうためには、改めてその正しさを証明する必要があるのです。
最後に直角三角形について考えていきましょう。直角三角形の直角に対する辺は斜辺といいます。また直角三角形は「三角形の合同条件」に加えて、次の2つの特別な合同条件を使うことができます。(1) 斜辺と1つの鋭角がそれぞれ等しい。 (2) 斜辺と他の1辺がそれぞれ等しい。 2つの直角三角形の合同を考える時は、この特別な合同条件を上手く活用しましょう。
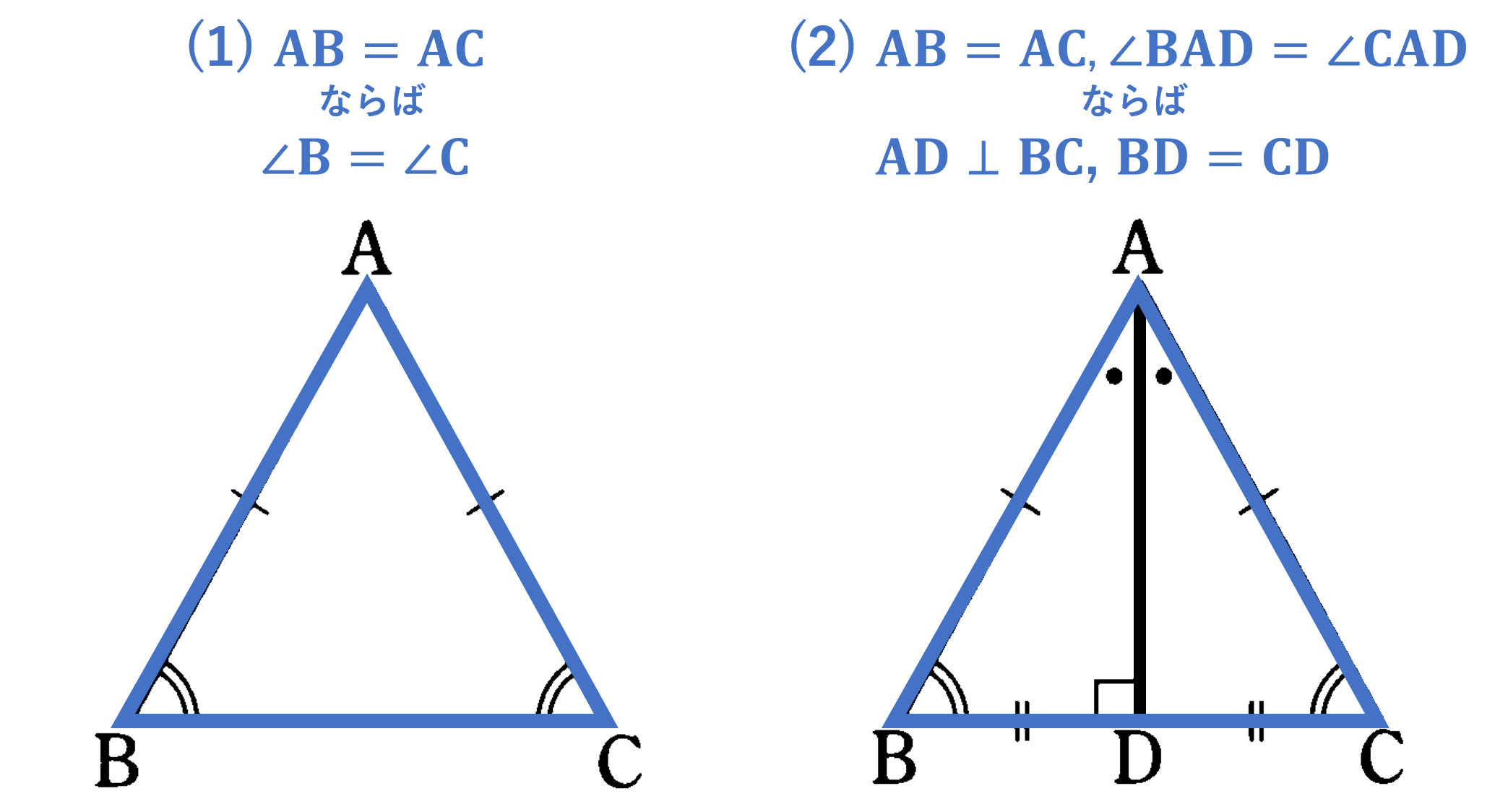
二等辺三角形の定義:2辺が等しい三角形
【定理】
(1) ${\rm AB}={\rm AC}$ ならば $\angle {\rm B}=\angle {\rm C}$
(2) ${\rm AB}={\rm AC}$, $\angle {\rm BAD}=\angle {\rm CAD}$ ならば ${\rm AD} \perp {\rm BC}$, ${\rm BD}={\rm CD}$
(3) $\angle {\rm B}=\angle {\rm C}$ ならば ${\rm AB}={\rm AC}$
【定理】
${\rm \triangle{ABC}}$ で ${\rm AB}={\rm BC}={\rm CA}$ $\iff$ $\angle {\rm A}=\angle {\rm B}=\angle {\rm C}$
直角三角形の定義:1つの内角が直角である三角形
直角三角形の合同条件:一般の合同条件の他に(1)(2)いずれかが等しい時にも合同。 (1) 斜辺と1つの鋭角 (2) 斜辺と他の1辺
四角形
本節では四角形、特に平行四辺形の性質についてみていきます。四角形の向かい合う辺を対辺向かい合う角を対角といいます。平行四辺形は以下のように定義づけられています。「平行四辺形とは2組の対辺がそれぞれ平行な四角形のことである。」平行四辺形 ${\rm ABCD}$ を ${\rm ▱ABCD}$ と表すこともあります。平行四辺形の性質(定理)として次の3つがあります。(1) 2組の対辺はそれぞれ等しい。 (2) 2組の対角はそれぞれ等しい。 (3) 対角線はそれぞれの中点で交わる。 これらの性質は「平行線と錯覚・対頂角・同位角」や「合同な図形」の知識を利用することで証明することができますので、1度確認しておきましょう。次に平行四辺形になるための条件についてみていきましょう。四角形は次のいずれかが成り立てば平行四辺形となります。(1) 2組の対辺がそれぞれ平行。…(定義) (2) 2組の対辺がそれぞれ等しい。 (3) 2組の対角がそれぞれ等しい。 (4) 対角線がそれぞれの中点で交わる。 (5) 1組の対辺が平行でその長さが等しい。
続いて、特別な平行四辺形である「長方形」「ひし形」「正方形」についてみていきます。それぞれの図形の定義は次の通りです。「長方形とは、4つの角が全て等しい四角形のことである」もしくは「長方形とは、4つの角が全て直角である四角形のことである」。「ひし形とは、4つの辺が全て等しい四角形のことである。」「正方形とは、4つの角が全て等しく、4つの辺が全て等しい四角形のことである」もしくは「正方形とは、4つの角が全て直角で、4つの辺が全て等しい四角形のことである。」 これらの定義からもわかるように、長方形やひし形は平行四辺形の特別な場合と考えることができます。また、長方形であり、ひし形でもある四角形が正方形です。
最後に、それぞれの図形の対角線の性質について考えてみましょう。長方形は対角線が等しくなります。ひし形の対角線は垂直に交わります。また、長方形の対角線の性質から考えると、直角三角形の斜辺の中点はこの三角形の3つの頂点から等しい距離になることが分かります。これらの性質を上手く活用して、図形に関する問題を工夫して解決していきましょう。
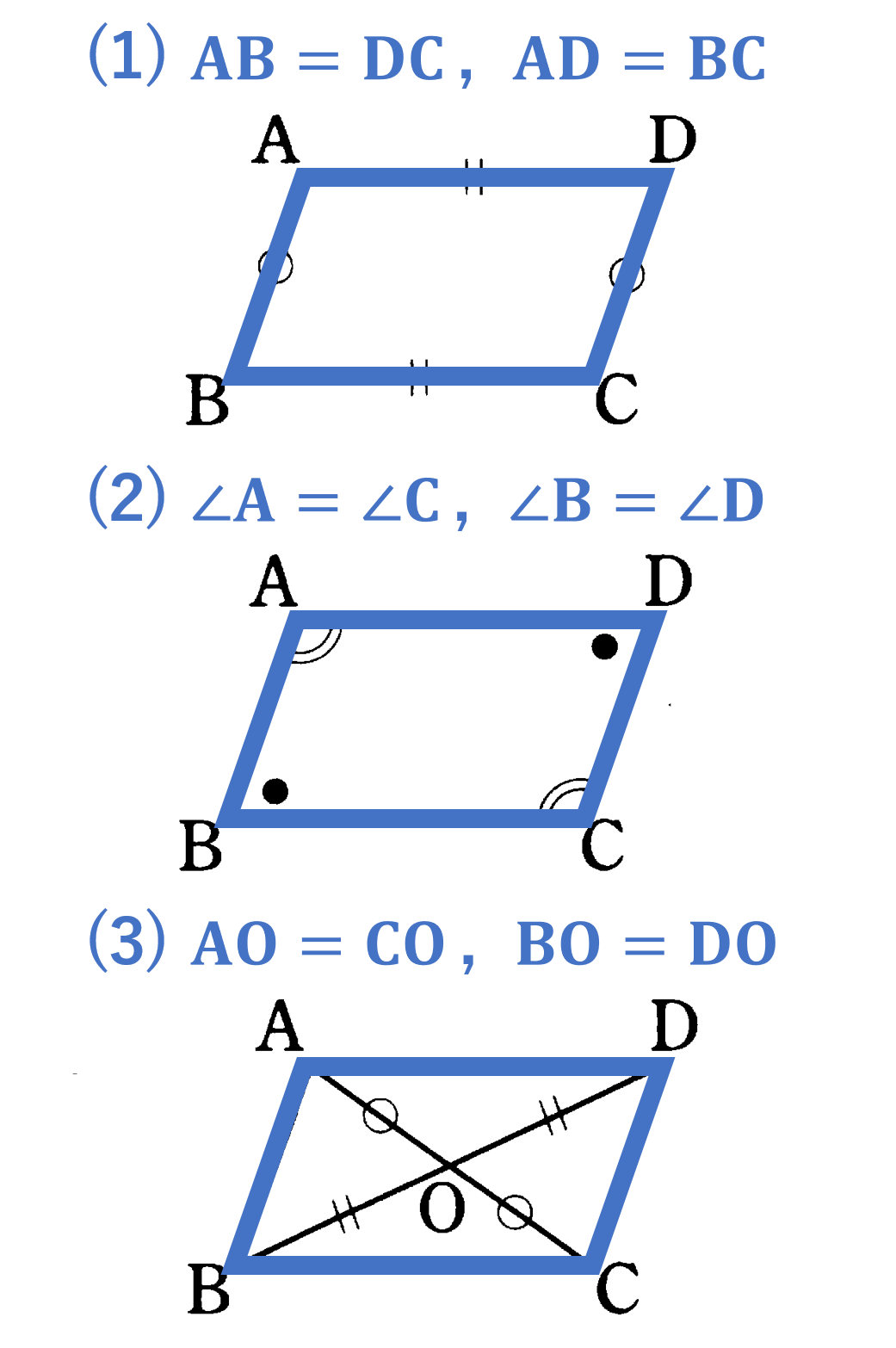
平行四辺形の定義:2組の対辺がそれぞれ平行な四角形
【定理】
(1) 2組の対辺はそれぞれ等しい。 ${\rm AB}={\rm DC},{\rm AD}={\rm BC}$
(2) 2組の対角はそれぞれ等しい。 $\angle {\rm A}=\angle {\rm C},\angle {\rm B}=\angle {\rm D}$
(3) 対角線がそれぞれの中点で交わる。 ${\rm AO}={\rm CO},{\rm BO}={\rm DO}$
平行四辺形になる条件:
(1) 2組の対辺がそれぞれ平行である。(=定義)
(2) 2組の対辺がそれぞれ等しい。
(3) 2組の対角がそれぞれ等しい。
(4) 対角線がそれぞれの中点で交わる。
(5) 1組の対辺が平行でその長さが等しい。
長方形:4つの角が等しい四角形。
(1) 長方形は平行四辺形。
(2) 1つの角が $90^{\circ}$
(3) 対角線の長さが等しい。

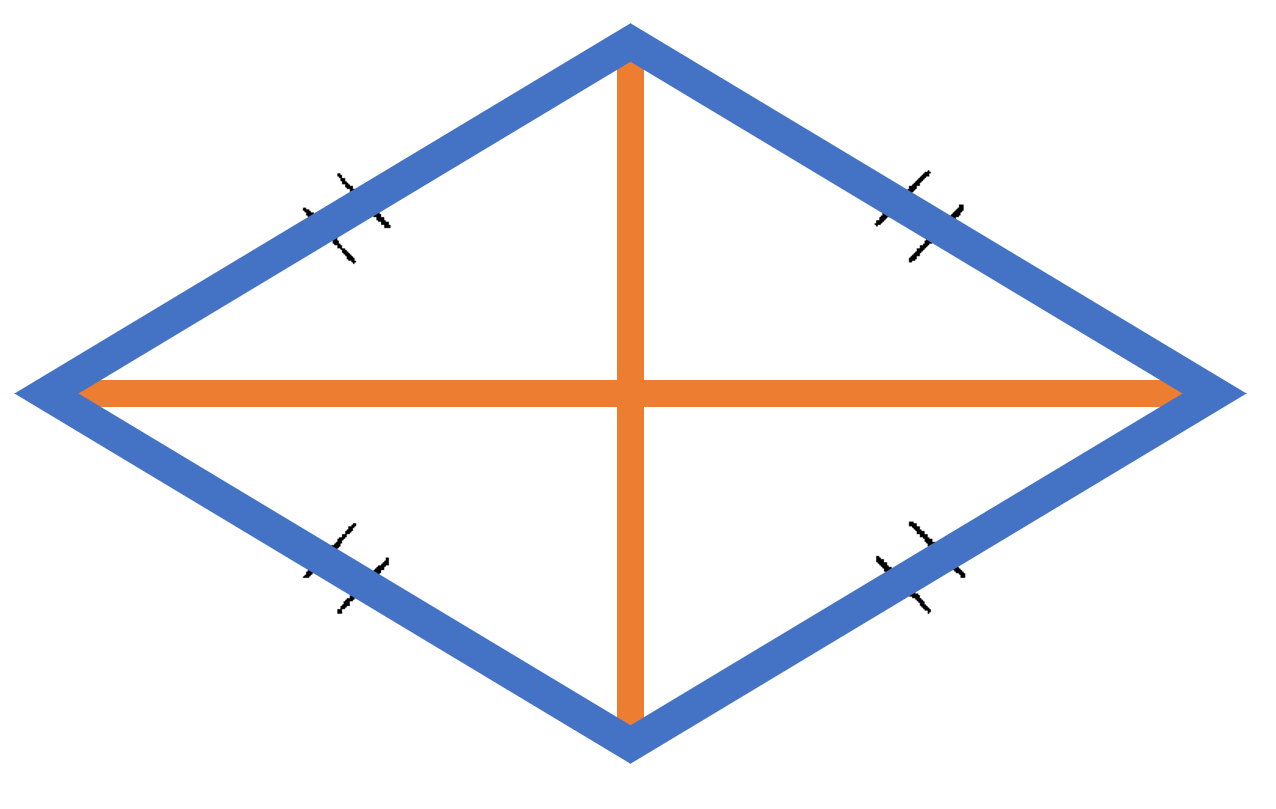
菱形:4つの辺が等しい四角形。
(1) 菱形は平行四辺形の特別な例(つまり菱形も平行四辺形)。
(2) 対角線が垂直に交わる。
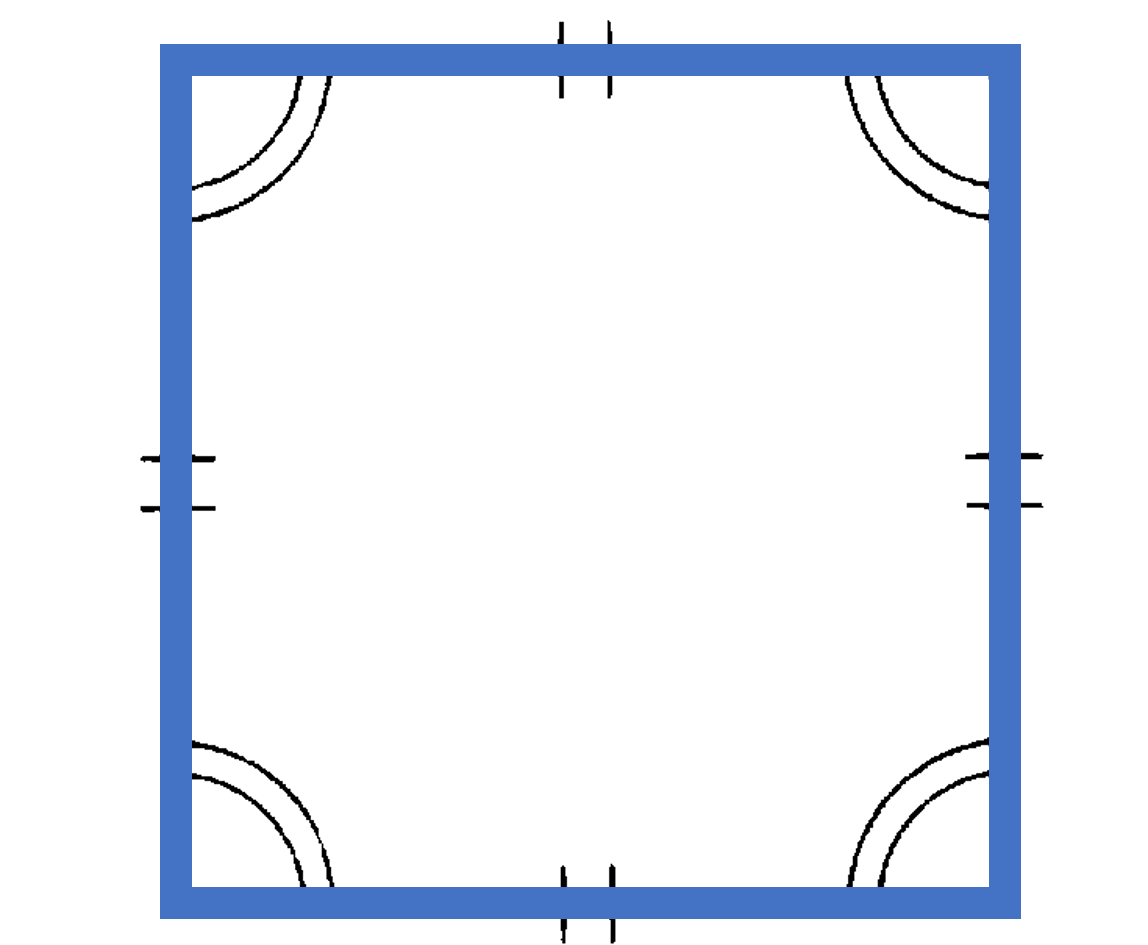
正方形:4つの角が等しく4つの辺が等しい四角形。
(1) 長方形と菱形の性質をもつ。
(2) 対角線が互いに垂直で長さが等しい。
平行線と面積
本節では、多角形の面積を変えずに平行線の性質を利用して変形する方法を考えてみましょう。下図のような、底辺 ${\rm BC}$ を共有し ${\rm BC}$ に平行な直線 $\ell$ 上に頂点を持つ ${\rm \triangle{ABC}}$, ${\rm \triangle{A’BC}}$, ${\rm \triangle{A^{\prime \prime}BC}}$ の面積を考えると、これらの三角形はみな、底辺が同じで高さが等しいため、面積が同じになります。このように、平行線を利用して、面積を変えずに図形を変形することができます。この変形を習得することで、一見計算できないような図形の面積を簡単に求めることができることがあります。演習重ねて、平行線と面積について、正しく理解しておきましょう。
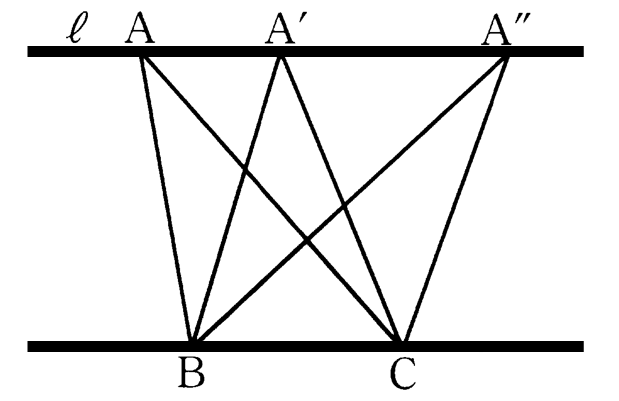
面積が等しい三角形:辺 ${\rm BC}$ を共有する ${\rm \triangle{PBC}}$ と ${\rm \triangle{ABC}}$ において
${\rm PA / \! \! / BC}$$\iff$${\rm \triangle{PBC}=\triangle{ABC}}$
中2 > 6章:確率
本章では、サイコロやルーレットの目の出方やカードゲームの手札など、偶然に左右されることがらの起こりやすさについて、実験や計算によって求める方法について考えていきましょう。身近でよくみかける確率としては、天気予報があります。天気予報は、たとえば降水確率 $30%$ は「過去に同じ気象条件が $100$ 回あったとしたときに、$30$ 回雨が降った」ということを表しているのです。なので、あくまで雨が降るかどうかを示したもので、雨の強さまでは、降水確率からは分かりません。さて、今日の降水確率が $30%$ のとき、あなたは傘を持ってでかけますか?確率を勉強すると、そのヒントや答えが見つかるかもしれません。
場合の数
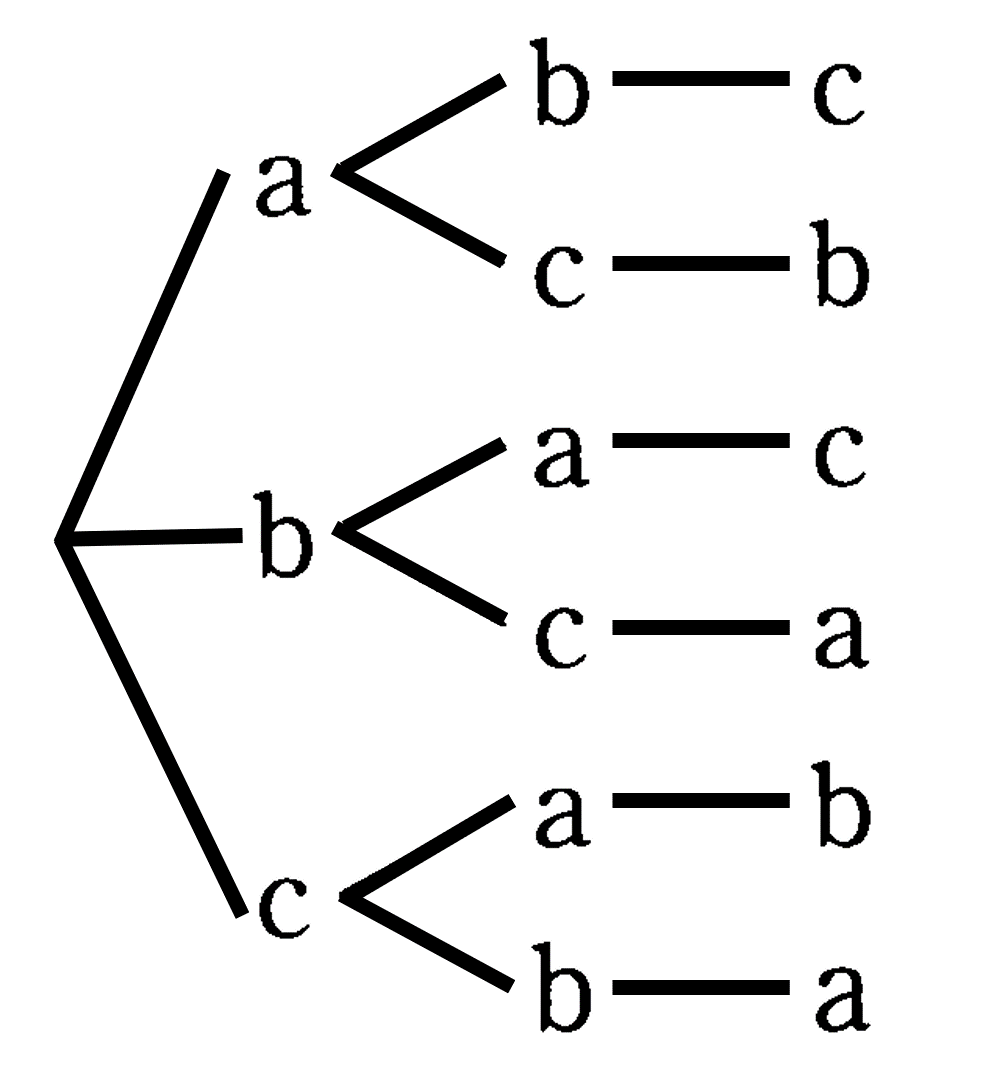
本節では、確率の基礎の理解の準備として、場合の数の考え方を正しく理解しましょう。
場合の数の数え方:
(1) 起こりうる場合の全部をもれなく重複なく数えあげる。それには全ての場合を順序よく整理して並べる。
(2) 樹形図や表を用いる。$a,b,c$ を1列に並べる $\to$ 起こりうる場合を樹状に整理して列挙した図を樹形図という。
数学が面白くなる動画―13
確率を知らないとゲームに負ける?確率はゲームに勝つための強力な武器になるのです。
確率
本節では、ことがらの起こりやすさを数で表現する方法や、それを利用して物事を判断することについて考えてみましょう。例えば「コインを投げて表が出る」ということがらのように、その結果が偶然に左右される実験や観察を行う時に、そのことがらが起こると期待される程度を数で表現したものを、そのことがらの起こる確率といいます。確率が $p$ であるということは「同じ実験や観察を何度も繰り返すと、そのことがらの起こる相対度数(コインが表になる相対度数=$\frac{表向きになった回数}{コインを投げた回数}$)が $p$ に限りなく近づくという意味をもっています。例えばコインを投げる場合では、表が出ることと裏が出ることは同じ程度に期待できます。このようなとき、どの結果が起こることも同様に確からしいといいます。反対に、いかさまのコインで、どちらかの面が出やすいような仕掛けがされている場合は、同様に確からしいとはいえません。数学では特別な条件が与えられない限り、サイコロやコインなどは正しく作られているものとして扱います。
ここから、具体的な確率の計算方法について考えてみましょう。ある実験または観察を行うときに、起こりうる場合が全部で $n$ 通りあり、どの場合が起こることも同様に確からしいとします。そのうち、あることがら ${\rm A}$ の起こる場合が $a$ 通りあるとき、ことがら ${\rm A}$ の起こる確率 $p$ は $p=\frac{a}{n}$ で求めることができます。つまり、確率 $p=\frac{ことがらAの起こる場合の数}{起こり得る全ての場合の数}$ ということです。また、確率 $p$ のとりうる値は $0≦p≦1$ の範囲にあります。「必ず起こる」確率は $1$ 「決して起こらない」確率は $0$ となります。そして一般に、ことがら $A$ の起こらない確率は $(Aの起こらない確率)=1-(Aの起こる確率)$ で求めることができます。これらの知識を活用して、いろいろなことがらの確率を正しく効率的に計算できるように練習しましょう。
確率:あることがらが起こることが期待されている程度の数。
同様に確からしい:全ての場合の起こり方が同じ程度に期待されていること。
(1) 確率 $=\frac{ことがらAの起こる場合の数}{起こり得る全ての場合の数}$
例
大小2つのサイコロを投げるとき、和が $4$ になる確率を求める。起こりうる場合は全部で $6 \times 6 =36$ 通りあり、どの場合が起こることも同様に確からしい。このうち、出た目の数の和が $4$ となるのは $(1,3),(2,2),(3,1)$ の $3$ 通りあるため、求める確率は $\frac{3}{36}=\frac{1}{12}$ となる。
例
3枚のコインを投げるとき少なくとも1枚は表が出る確率を求める。「少なくとも1枚は表が出る」というのは「3枚とも裏にはならない」と同じであることから、求める確率は全体から3枚とも裏になる確率を引けば求まる。よって $1-(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2})$$=1-\frac{1}{8}$$=\frac{7}{8}$ となる。
数学が面白くなる動画―14
クラスに同じ誕生日の人がいる確率はどのくらいでしょう?
数学が面白くなる動画―14.5
世界中を楽しませたモンティホール問題


