🔄 最終更新日 2021年5月29日 by takara_semi
2章:図形の性質
本章では「平面図形」「空間図形」について学習する.
第1節 平面図形
❶ 三角形の辺の比
(a) 三角形の角のニ等分線と比
三角形の内角を二等分する場合と,外角を二等分する場合,それぞれについて,相似を利用することで証明可能な「比に関する」以下の有用な定理が知られている.
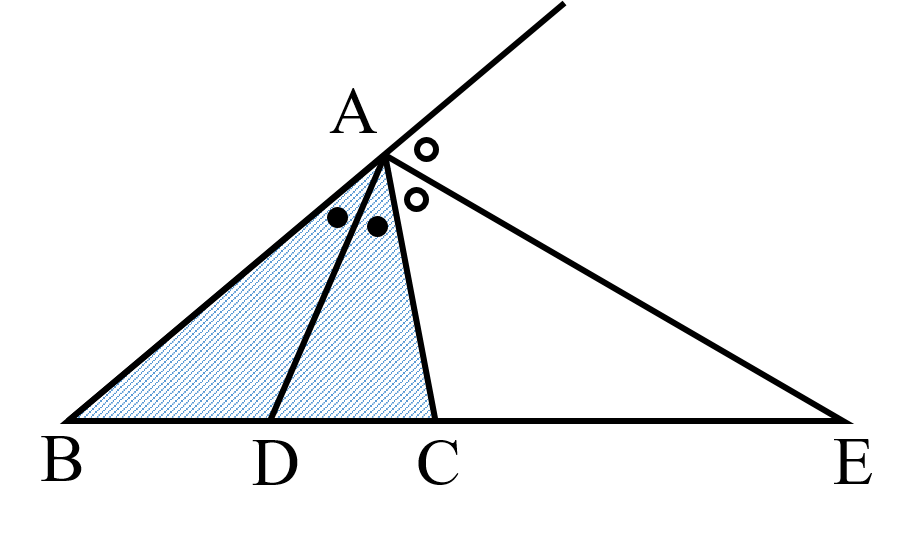
定理①:△ABC の ∠A の二等分線と辺 BC との交点は,辺 BC を $AB:AC$ に内分する.
$BD:DC=AB:AC$
定理②:$AB≠AC$ である △ABC の ∠A の外角の二等分線と辺 BC の延長との交点は,辺BC を $AB:AC$ に外分する.
$BE:EC=AB:AC$
❷ 三角形の外心・内心・重心
三角形の「外心」「内心」「重心」(補足として「垂心」)について,以下のような定理が知られている.それぞれの条件が与えられたときに,定理の図がすぐにイメージできるよう,理解を深めておくことが望ましい.
定理③:三角形の3辺の垂直二等分線は「外心」で交わる.
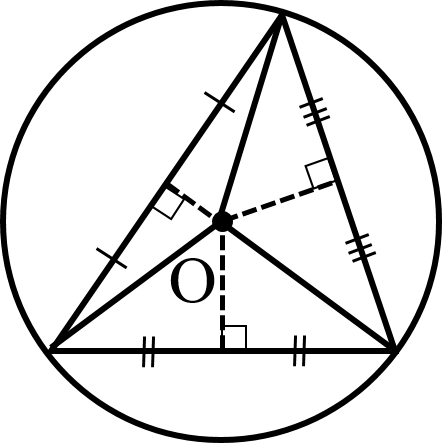
定理④:三角形の3つの内角の二等分線は「内心」で交わる.

定理⑤:三角形の3本の中線は「重心」で交わり,その点は各中線を 2:1 に内分する.

(a) 三角形の垂心
三角形の各頂点から向かい合う辺,またはその延長に下ろした垂線は「垂心」で交わる.
❸ チェバの定理・メネラウスの定理
(a) チェバの定理
三角形に関する比についての強力な定理として「チェバの定理」がある.後述する証明も理解しておくことが望ましい.
定理⑥:△ABC の内部に点 O がある.
頂点 A,B,C とO を結ぶ直線が,向かい合う辺とそれぞれ点 P,Q,R で交わるとき,以下の関係が成り立つ.
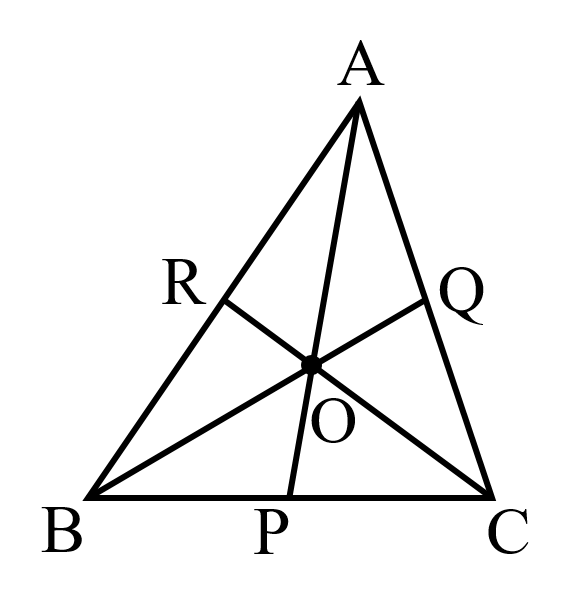
$\frac{AR}{RB}$$=\frac{△AOC}{△BOC}$,$\frac{BP}{PC}$$=\frac{△AOB}{△AOC}$, $\frac{CQ}{QA}$$=\frac{△BOC}{△AOB}$
となる.辺々掛け合わせると
$\begin{eqnarray}
\frac{AR}{RB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} &=& \frac{△AOC}{△BOC} \cdot \frac{△AOB}{△AOC} \cdot \frac{△BOC}{△AOB}\\
&=& \frac{△AOC \cdot △AOB \cdot △BOC}{△BOC \cdot △AOC \cdot △AOB}\\
&=& \frac{△AOC \cdot △AOB \cdot △BOC}{△AOC \cdot △AOB \cdot △BOC}\\
&=& 1
\end{eqnarray}$
となり,チェバの定理が導かれた.
(b) メネラウスの定理
三角形と直線に関する比についての強力な定理として「メネラウスの定理」がある.チェバの定理との共通点や差異を意識し,後述する証明も理解しておくことが望ましい.
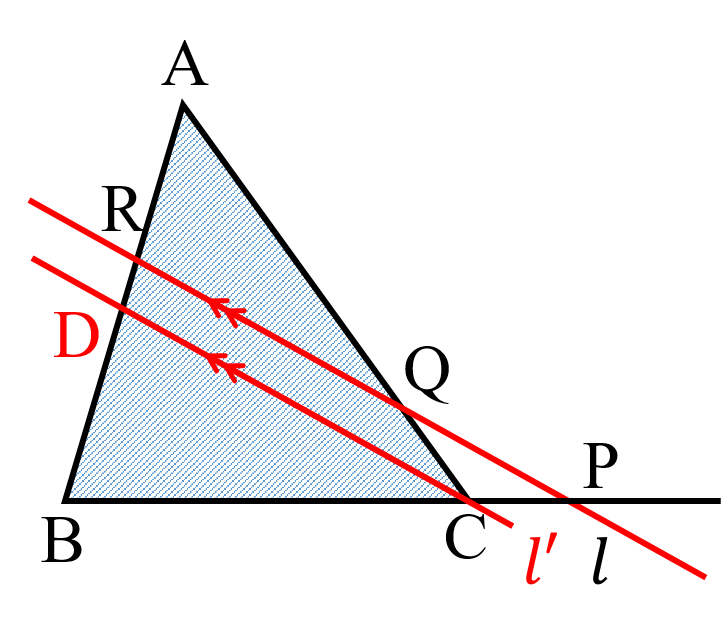
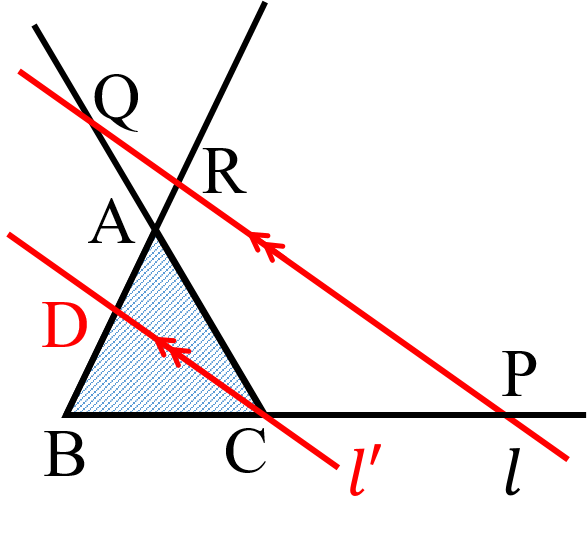
定理⑦:△ABC の辺 BC,CA,AB またはその延長が,三角形の頂点を通らない直線 $l$ と,それぞれ点 P,Q,R で交わるとき,次の関係が成り立つ.
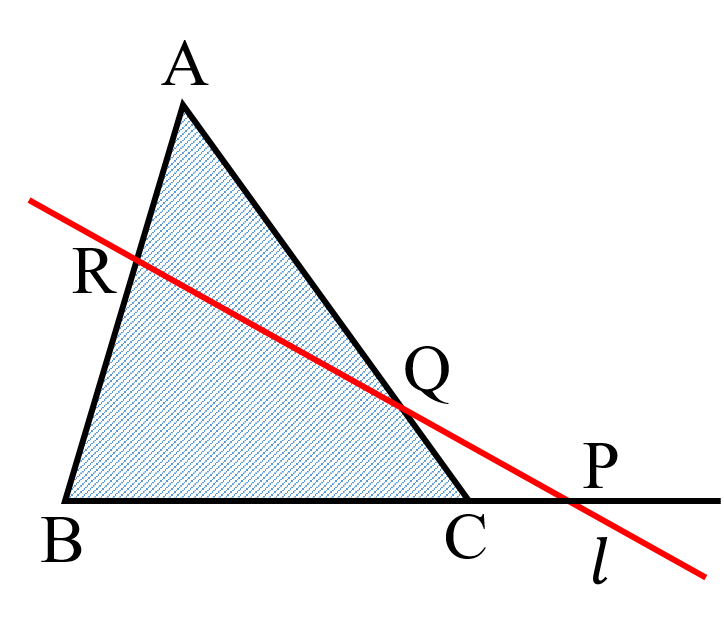

$BP:PC=BR:RD$,$CQ:QA=DR:RA$
つまり
$\frac{BP}{PC}=\frac{BR}{RD}$, $\frac{CQ}{QA}=\frac{DR}{RA}$
よって
$\begin{eqnarray}
\frac{AR}{RB} \cdot \frac{BP}{PC} \cdot \frac{CQ}{QA} &=& \frac{AR}{RB} \cdot \frac{BR}{RD} \cdot \frac{DR}{RA}\\
&=& \frac{AR \cdot BR \cdot DR}{RB \cdot RD \cdot RA}\\
&=& \frac{AR \cdot BR \cdot DR}{RA \cdot RB \cdot RD}\\
&=& \frac{AR \cdot BR \cdot DR}{AR \cdot BR \cdot DR}\\
&=& 1
\end{eqnarray}$
となり,メネラウスの定理が導かれた.
(c) チェバの定理の逆・メネラウスの定理の逆
「チェバの定理の逆」と「メネラウスの定理の逆」は次の通り.
❹ 三角形の面積と比
三角形の面積の比について,以下のことが知られている.
(i) 「高さが等しい2つの三角形の面積の比」=「底辺の長さの比」
(ii) 「底辺の長さが等しい2つの三角形の面積の比」=「高さの比」
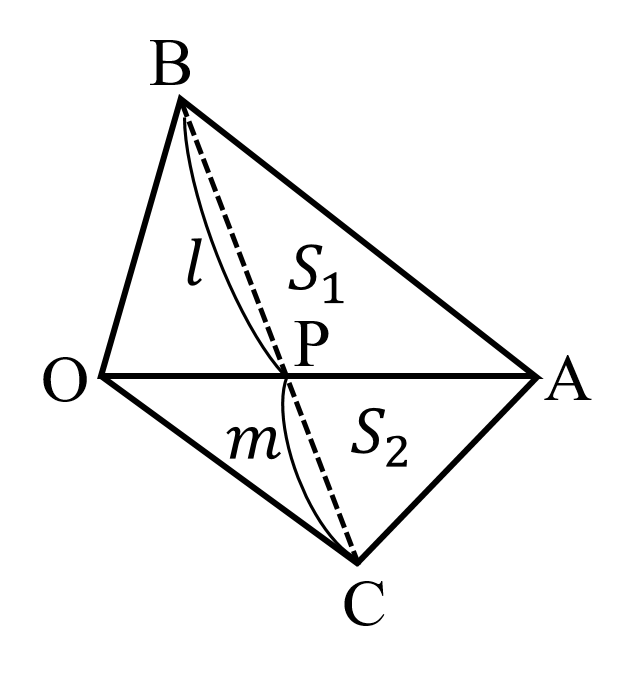
(iii) 底辺 OA を共有する △OAB,△OAC において,2直線 AO,BC が点 P で交わるとすると $△OAB:△OAC=PB:PC$ ($S_1:S_2=l:m$)
❺ 三角形の比と角
(a) 三角形の3辺の大小関係
1つの三角形において,3辺の大小関係について以下のことが知られている.
(ii) 2辺の長さの差は,他の1辺の長さよりも小さい.
(b) 三角形の存在条件
三角形の存在条件は,以下の通り.証明問題などで必要となることもあるため,正確に理解しておくこと(先述の「3辺の大小関係」と合わせて理解しておくと分かりやすい).
(ii) 3辺の長さ $a,b,c$ の中で,$a$ が最大であれば,三角形が存在するための条件は,$a<b+c$ が成り立つことである.
(c) 三角形の辺と角の大小関係
三角形の辺と角の大小関係について,以下の関係が知られている.
△ABC において,次が成り立つ.
$b=c ⇔ ∠B=∠C$
$b<c ⇔ ∠B<∠C$
❻ 円に内接する四角形
(a) 円周角の定理
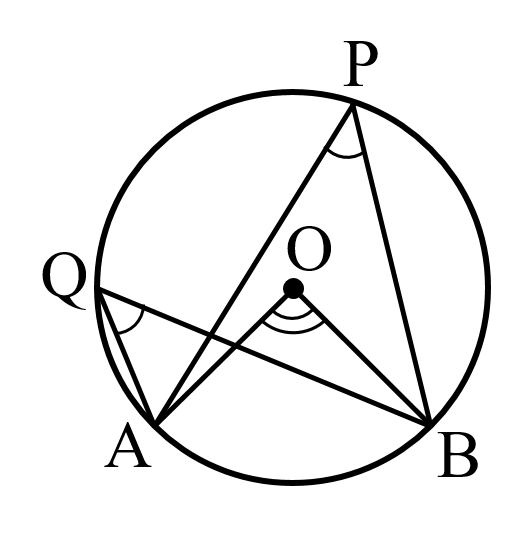
円周角の定理は以下の通り(中学数学で学習済みであるが,重要な定理のため再掲する).
1つの弧に対する円周角の大きさは一定であり,その弧に対する中心角の大きさの半分である.
また異なる3点 A,B,P について,次が成り立つ.
「点 P が線分 AB を直径とする円の周上にある」⇔「∠APB=$90^{\circ}$」
(b) 円周角の定理の逆
「円周角の定理の逆」は以下の通り.ある4点が同一円周上に位置するかどうかが分かる,有用な定理であるため,正確に理解しておくことが望ましい.
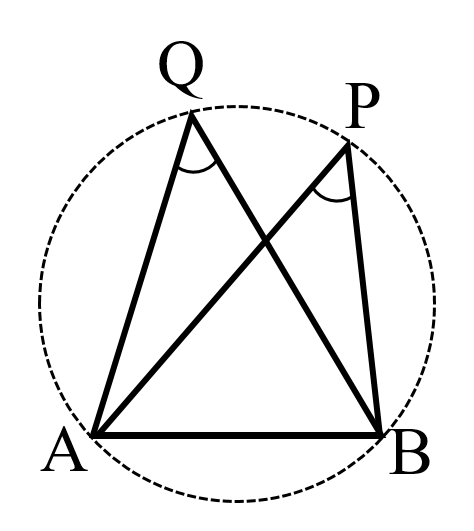
4点 A,B,P,Q について,点 P,Q が直線 AB に関して同じ側にあって∠APB=∠AQB ならば,4点 A,B,P,Q は 1つの円周上にある.
(c) 円に内接する四角形
円に内接する四角形について,以下の関係が知られている.
定理⑧:円に内接する四角形について,次の (i),(ii) が成り立つ.
(ii) 内角は,その対角の外角に等しい.
定理⑨:次の (i) または (ii) が成り立つ四角形は,円に内接する.
(ii) 内角が,その対角の外角に等しい.
❼ 円と直線
(i) 円 $O$ の周上の点 A を通る直線 $l$ について,次が成り立つ.
「直線 $l$ が点 A で円 $O$ に接する」 ⇔ 「OA$⊥l$」
(ii) 円の外部の1点からその円に引いた2つの接線の長さは等しい.
(a) 円の接線と弦の作る角
円の接線と弦の作る角について,以下の関係(接弦定理)が知られている.
(b) 方べきの定理
円と2直線が与えられたときに有用な「方べきの定理」は以下の通りである.
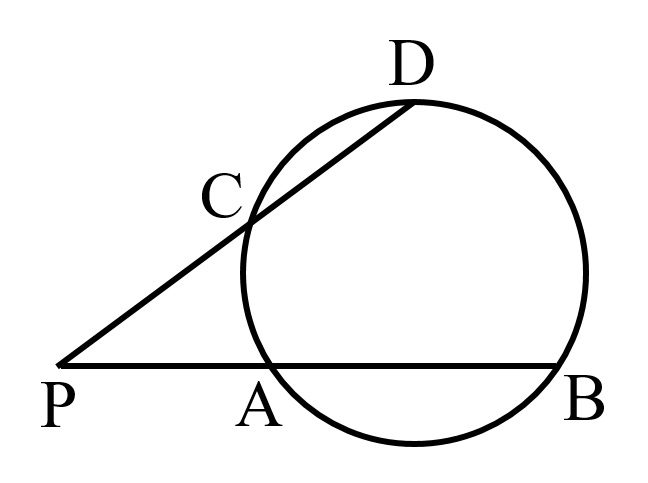
定理⑪:円の2つの弦 AB,CD の交点,またはそれらの延長の交点を P とするとき,以下の関係が成り立つ.

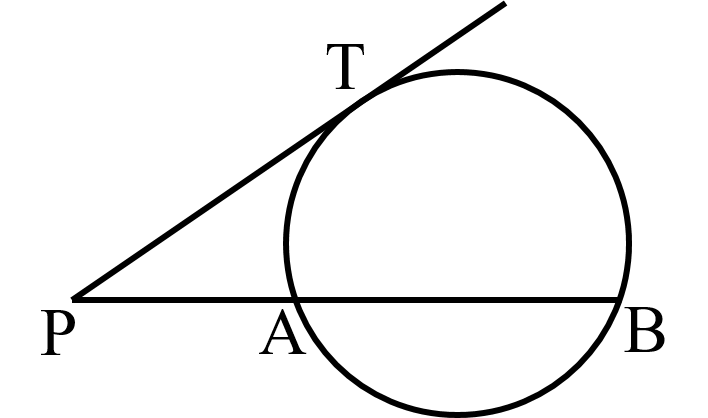
定理⑫:円の外部の点 P から円に引いた接線の接点を T とする.P を通ってこの円と 2点 A,B で交わる直線を引くと,以下の関係が成り立つ.
(c) 方べきの定理の逆 (定理⑪の逆)
「方べきの定理の逆」は「円周角の定理の逆」と同様,与えられた4点が同一円周上に存在するかどうかを調べることができる有用な定理であるため,正確に理解しておくことが望ましい.
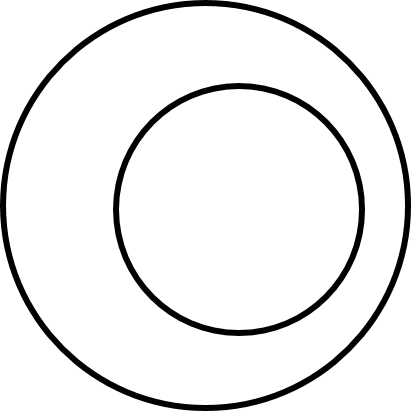
❽ 2つの円
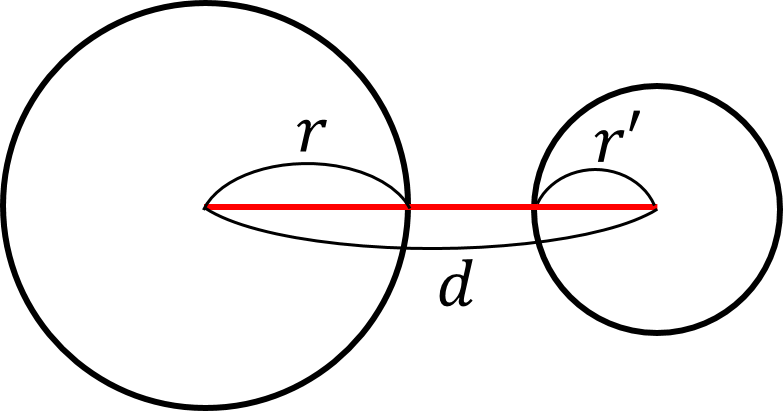
2つの円の位置関係は,$r>r’$ として,次の(i)~(v)の場合に分類できる.
(i) 一方が他方の外部にある
(ii) 外接する
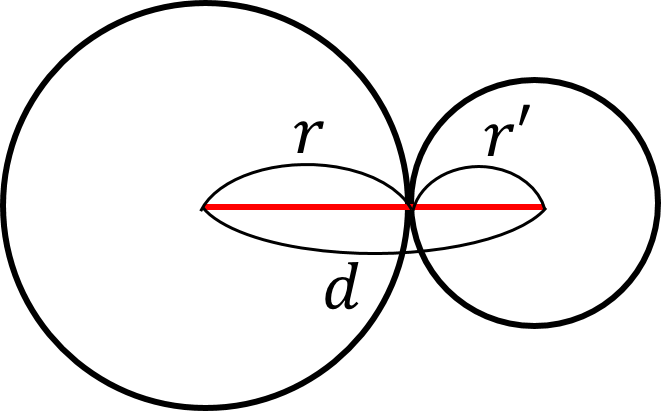
(iii) 2点で交わる

(iv) 内接する
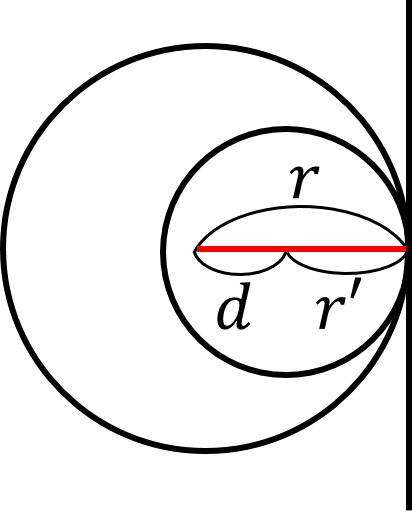
(v) 一方が他方の内部にある
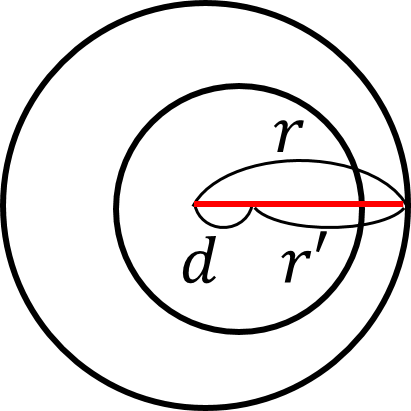
また,2つの円の両方に接する直線を,2つの円の「共通接線」という.2つの円の共通接線は,円の位置関係に応じて,次の(i)~(v)の場合に分類できる.
(i) 共通接線が4本ある

(ii) 共通接線が3本ある

(iii) 共通接線が2本ある
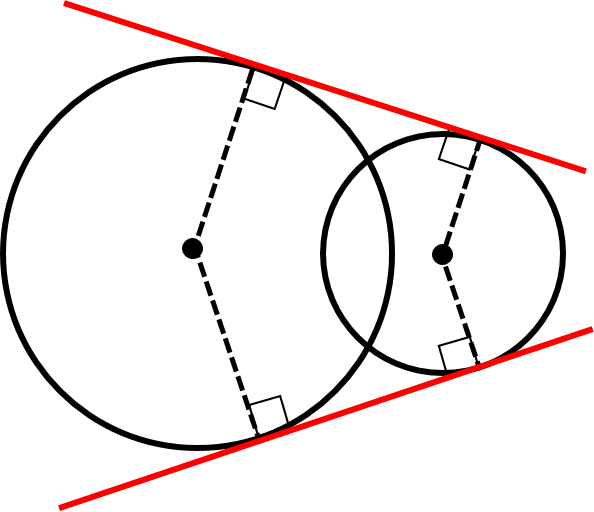
(iv) 共通接線が1本ある

(v) 共通接線がない
❾ 作図
作図は自由に道具を使って図を描く作業ではない.作図では「定規」と「コンパス」を用いて「(A)与えられた2点を通る直線を引くこと」「(B)与えられた1点を中心として,与えられた半径の円をかくこと」,これらの限られた操作だけで求められる図を描く作業をいう.つまり,(A)(B)の作業で必要となる点,直線,円を描き,与えられた条件を満たす図形を描くことが作図である.「2枚の定規を用いて平行線を引く」「定規の目もりで長さを測る」などの操作は,作図ではない.
第2節 空間図形
❶ 直線と平面
(a) 2直線の位置関係
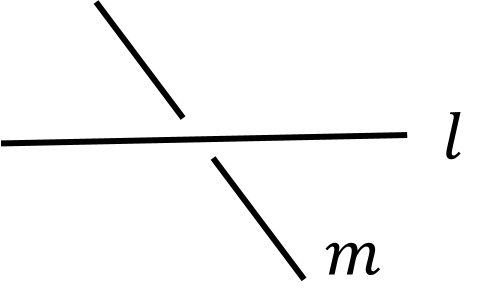
異なる2直線 $l$,$m$ の位置関係には,次の3つの場合がある.(i) 1点で交わる.(ii) 平行である $(l // m)$:2直線は1つの平面上にある.(iii) ねじれの位置にある:2直線は1つの平面上にない.ねじれの位置とは,下図のような位置関係を指す.
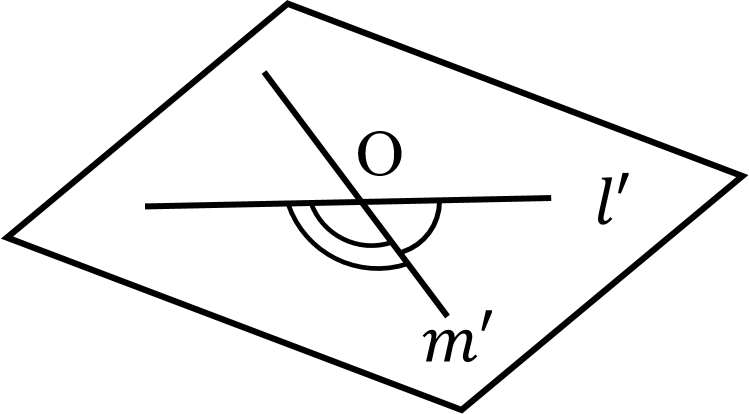
3直線 $l,m,n$ について $l // m$, $m // n$, ならば $l // n$ である.また,2直線 $l,m$ が平行でないとき,任意の1点 $O$ を通り,$l,m$ に平行な直線を,それぞれ $l’,m’$ とする.このとき $l’$ と $m’$ のなす角を2直線 $l$,$m$ のなす角という(つまり下図のようにして2直線の「なす角」を定義づけることができる).
2直線 $l$,$m$ のなす角が直角のとき「$l$ と$m$ は垂直である」という($l⊥m$).また,平行な2直線の一方に垂直な直線は,他方にも垂直となる.「ねじれの位置」があることによって,一見複雑に感じられる「空間における直線」の性質だが,平面における直線の性質との共通点も多く,そのことを理解すれば,平面⇔空間の変換は容易になる.
(b) 直線と平面の位置関係
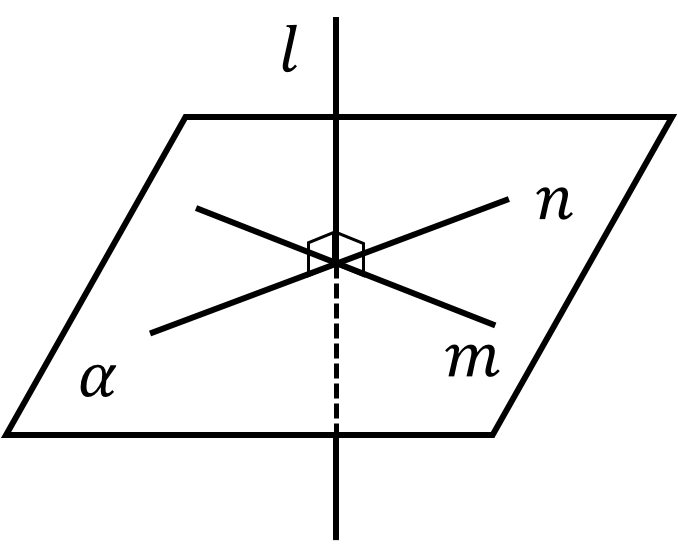
直線 $l$ と平面 $\alpha$ の位置関係には,次の3つの場合がある.(i) $l$ は $\alpha$ に含まれる.(ii) 1点で交わる: $l$ と $\alpha$ は共有点をもつ.(iii) 平行である ($l$ // $\alpha$).(i)(ii)の場合は,$l$ と $\alpha$ は共有点をもち,(iii)の場合は,共有点をもたない.また直線 $l$ が,平面 $\alpha$ 上のすべての直線に垂直であるとき「$l$ は $\alpha$ に垂直である」または「$l$ は $\alpha$ に直交する」という($l⊥\alpha$).このとき,$l$ を平面 $\alpha$ の垂線という.また,直線 $l$ が,平面 $\alpha$ 上の交わる2直線 $m,n$ に垂直ならば,直線 $l$ は平面 $\alpha$ に垂直であるという(下図).
(c) 2平面の位置関係
異なる2平面 $\alpha$,$\beta$ の位置関係は「交わる」もしくは「平行($\alpha // \beta$)」であり,2平面が交わる部分を「交線」という.
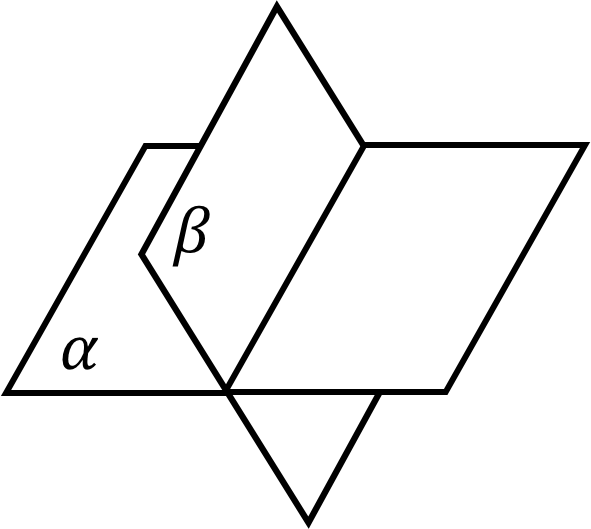

交わる2平面の交線上の点から,各平面上に,交線に垂直に引いた2直線のなす角を「2平面のなす角」という.
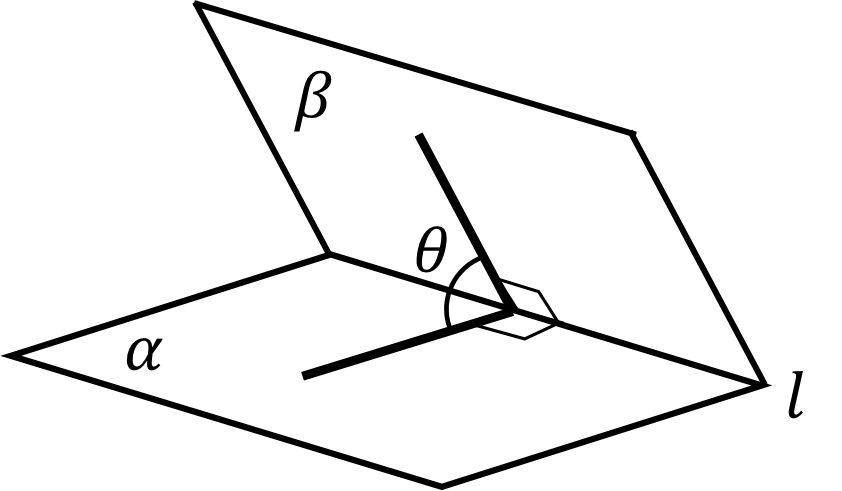
2平面 $\alpha,\beta$ のなす角が直角のとき,$\alpha,\beta$ は「垂直」または「直交」といい,$\alpha⊥\beta$ と書く.また,平面 $\alpha$ に垂直な直線を含む平面は,$\alpha$ に垂直となる.
(d) 三垂線の定理
平面 $\alpha$ とその上の直線 $l$ があるとき,$\alpha$ 上にない点 A,$\alpha$ 上にあるが $l$ 上にない点O,および $l$ 上の点Bについて,次の「三垂線の定理」が成り立つことが知られている.
(i) OA⊥$\alpha$,OB⊥$l$ ならば AB⊥$l$
(ii) OA⊥$\alpha$,AB⊥$l$ ならば OB⊥$l$
(iii) OB⊥$l$,AB⊥$l$,OA⊥OB ならば OA⊥$\alpha$

❷ 空間図形と多面体
(a) 多面体
三角柱,四角錐などのように,平面だけで囲まれた立体を「多面体」という.多面体の中でも「へこみのない多面体」を「凸多面体」という.さらに,次の(i),(ii)を満たす凸多面体を「正多面体」という.
(i) 各面はすべて合同な正多角形である.
(ii) 各頂点に集まる面の数はすべて等しい.
正多面体は5種類しかないことが知られている.
また,凸多面体において,その頂点.辺,面の数の関係について,以下の定理が知られている.
凸多面体の頂点の数を $v$,辺の数を $e$,面の数を $f$ とすると,以下の関係が成り立つ.
(b) 正多面体から切り取った立体
「正四面体」は,立方体の各辺の隣り合わない頂点を結ぶことで,立方体の内部に作ることができ,「正八面体」は立方体の各面の対角線の交点を頂点とし,隣り合った面どうしの頂点を結ぶことで,立方体の内部に作ることができる(立方体の切り取りの問題の場合,これらの知識を知っているだけで容易に解けることもある).

