🔄 最終更新日 2021年5月19日 by takara_semi
第4章:図形と計量
本章では「三角比」「三角形への応用」について学習する.
第1節:三角比
❶ 三角比
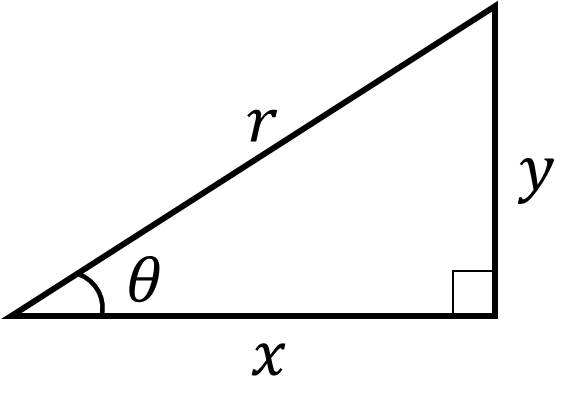
「正弦」「余弦」「正接」はそれぞれ,以下の図のような直角三角形において,次のように定義される.
$\cos{\theta} = \frac{x}{r}$ (余弦)
$\tan{\theta} = \frac{y}{x}$ (正接)
つまり三角比を利用すれば,$y=r \sin{\theta}$,$x=r \cos{\theta}$,$y=x \tan{\theta}$ として, $x,y$ の値を求めることができる.
❷ 三角比の相互関係
三角比は,その定義から,以下のような相互関係を容易に導くことができる.これらの関係式は頻繁に利用するため,暗記しておくことが望ましい.
(b) $\sin^2{\theta}+\cos^2{\theta}=1$ (三角比の定義および三平方の定理より)
(c) $1+\tan^2{\theta} = \frac{1}{\cos^2{\theta}}$ ((b)の両辺を $\cos^2{\theta}$ で割る)
❸ 三角比の拡張
座標を用いた三角比の定義は,下図において ∠AOP$=\theta$,OP$=r$,P$(x, y)$ として $\sin{\theta} = \frac{y}{r}$, $\cos{\theta} = \frac{x}{r}$, $\tan{\theta} = \frac{y}{x}$ となる.これは先述した三角比の定義と一致する.
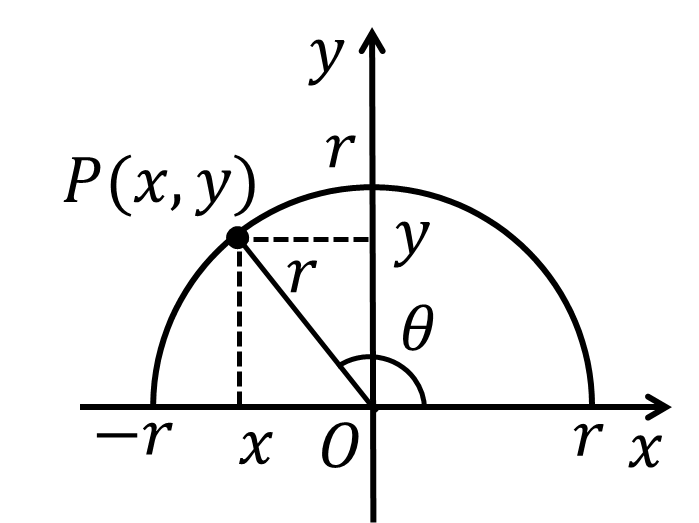
また,$\theta$ が $90^{\circ}$, $180^{\circ}$ 異なる場合の三角比には以下のような関係が成り立つ(図を用いて確認可能.また後に学ぶ「加法定理」を利用しても証明可能).
$\cos{(90^{\circ}-\theta)} = \sin{\theta}$
$\tan{(90^{\circ}-\theta)} = \frac{1}{\tan{\theta}}$
$\cos{(180^{\circ}-\theta)} = -\cos{\theta}$
$\tan{(180^{\circ}-\theta)} = -\tan{\theta}$
※ 現状では丸暗記(もしくは図を描いての確認)になってしまうかもしれないが「加法定理」を学べば,暗記に頼らず,容易に上記の関係を導けるようになる.
第2節:三角形への応用
❶ 正弦定理
正弦($\sin$)定理は以下の通り.
△ABC の外接円の半径を $R$ とすると
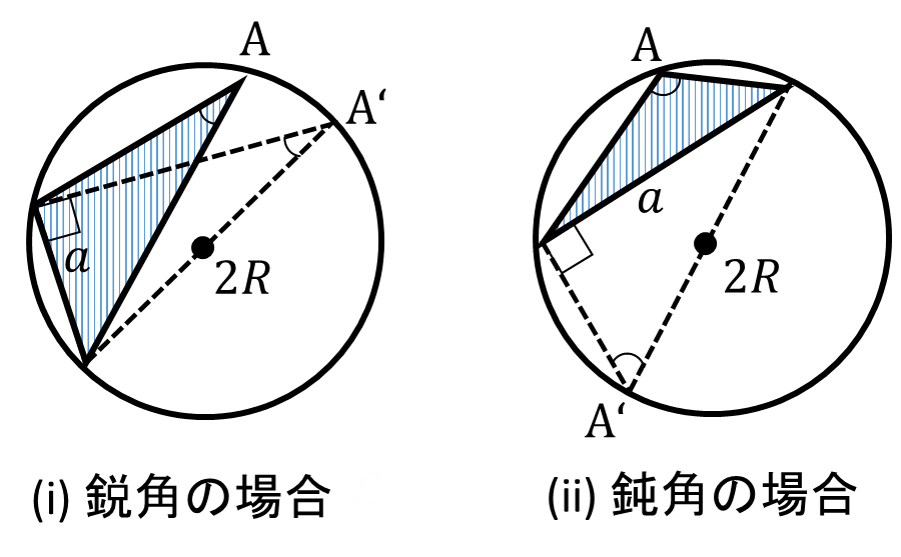
正弦定理の上図を用いて証明できる.
(i) 鋭角の場合:
円周角の定理より ∠A=∠A'($A=A’$) であるので $\sin{A}$$=\sin{A’}$$=\frac{a}{2R}$ となり $2R=\frac{a}{\sin{A}}$ が導かれた.その他の角でも同様の関係が成り立つため(鋭角の場合.鈍角の場合は(ii)の手順で証明する) $\frac{a}{\sin{A}}$$=\frac{b}{\sin{B}}$$=\frac{c}{\sin{C}}$$=2R$ がいえる.
(ii) 鈍角の場合:
円に内接する四角形の向かい合う角の和は $180^{\circ}$ となるため ∠A=$180^{\circ}$-∠A'($A=180^{\circ}-A’$) となる.ゆえに $\sin{A}$$=\sin{(180^{\circ}-A’)}$$=\sin{A’}$$=\frac{a}{2R}$ となり $2R=\frac{a}{\sin{A}}$ が導かれた.その他の角でも同様の関係が成り立つため(鈍角の場合.鋭角の場合は(i)の手順で証明する) $\frac{a}{\sin{A}}$$=\frac{b}{\sin{B}}$$=\frac{c}{\sin{C}}$$=2R$ がいえる.
❷ 余弦定理
余弦($\cos$)定理は以下の通り.
△ABCにおいて
$b^2=c^2+a^2-2ca \cos{B}$
$c^2=a^2+b^2-2ab \cos{C}$
つまり
$\cos{B}=\frac{c^2+a^2-b^2}{2ca}$
$\cos{C}=\frac{a^2+b^2-c^2}{2ab}$
∠A($A$)について $b^2+c^2>a^2$ のとき $A$ は鋭角,$b^2+c^2=a^2$ のとき $A$ は直角,$b^2+c^2<a^2$ のtき $A$ は鈍角となる.
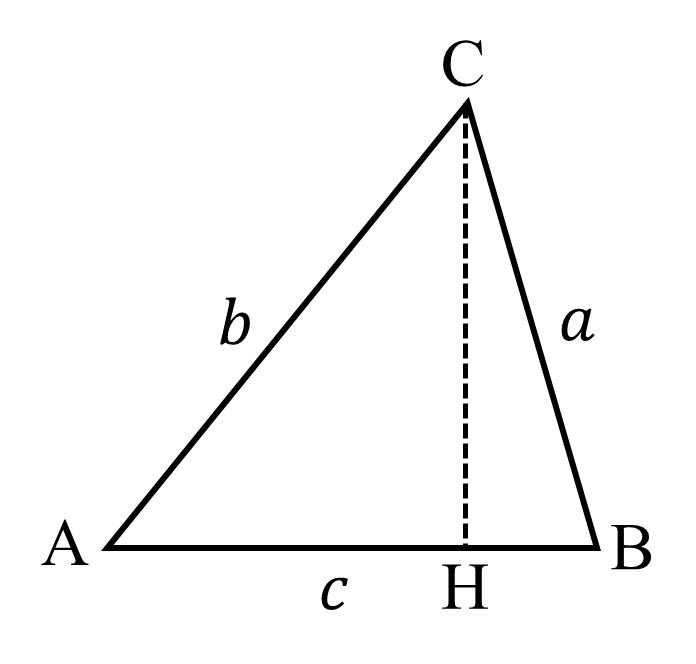
余弦定理は上図を用いて証明できる.
点Cから辺ABに下ろした垂線と辺ABとの交点をHとする.∠Aに注目して,直角三角形CBHにおいて三平方の定理を用いると
CB^2 &=& CH^2+HB^2 \\
a^2 &=& (b\sin{A})^2+(c-b\cos{A})^2 \\
&=& b^2\sin^2{A}+c^2-2bc\cos{A}+a^2\cos^2{A} \\
&=& b^2(\sin^2{A}+\cos^2{A})+c^2-2bc\cos{A} \\
&=& b^2+c^2-2bc\cos{A}
\end{eqnarray}$
同様に $b,c$ についての公式も導くことができる.また $A$ が鋭角でも鈍角でも同様の結果を得ることができる.
❸ 正弦定理と余弦定理の応用
三角形の辺と角について考える.三角形の6つの要素(3辺,3つの角)のうち,少なくとも1つの辺を含む3つの要素が与えられたとき,残りの要素を求めることができる.
次に三角形の辺と角の大小関係について考える.三角形の2辺の大小関係は,その向かい合う角の大小関係と一致する.△ABC において,たとえば $b<c$ であれば $B<C$ となる.よって,三角形の最大の辺に向かい合う角が,その三角形の最大の角となる.これは直感的にも正しいことが分かる.
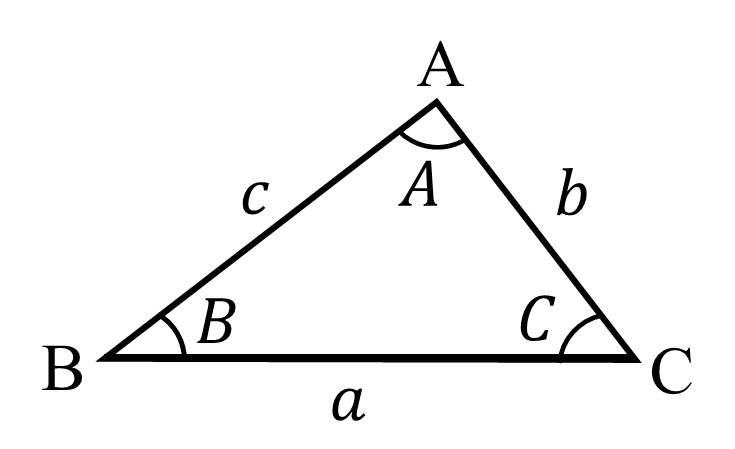
三角形△ABC の面積 $S$ は,次の式で求められる.
$S=\frac{1}{2}ca \sin{B}$
$S=\frac{1}{2}ab \sin{C}$
また三角形△ABC の面積を $S$ ,内接円の半径を $r$ とすると
S &=& a \times r \times \frac{1}{2} + b \times r \times \frac{1}{2} + c \times r \times \frac{1}{2} \\
&=& \frac{1}{2}r(a+b+c)
\end{eqnarray}$
としても面積 $S$ を計算できる.
❹ 空間図形への応用
(a) 線分の長さや角の大きさは,三角形の辺や角としてとらえ,三平方の定理や正弦定理,余弦定理を利用する。
(b) 角錐の体積 底面積 $S$,高さ $h$ の角錐の体積 $V$ は $V=\frac{1}{3}Sh$
※ 後に学ぶ「積分」を利用することで証明できる.
発展・応用
❶ ヘロンの公式
三角形の面積 $S$ は,3辺の長さがそれぞれ分かっている場合「ヘロンの公式」によって求めることができる.
3辺の長さが $a,b,c$ である △ABC の面積 $S$ は $2s=a+b+c$$(s=\frac{(a+b+c)}{2})$ とすると
ヘロンの公式は利用頻度がそれほど多くないため忘れてしまいがちであるが,強力な公式ではある.そのため,公式を忘れてしまっても,導けるようにしておくことが望ましい.以下のように式を変形することで証明可能である.
S &\mathop{=}^{(1)}& \frac{1}{2}ab \sin{C} \\
&\mathop{=}^{(2)}& \frac{1}{2}ab \sqrt{1-\cos^2{C}} \\
&\mathop{=}^{(3)}& \frac{1}{2}ab \sqrt{1-\{\frac{a^2+b^2-c^2}{2ab}\}^2}…(*) \\
&=& \frac{1}{2}ab \sqrt{\frac{(2ab)^2-(a^2+b^2-c^2)^2}{(2ab)^2}} \\
&=& \frac{1}{4} \sqrt{(2ab)^2-(a^2+b^2-c^2)^2} \\
&\mathop{=}^{(4)}& {\scriptsize \frac{1}{4} \sqrt{(2ab+a^2+b^2-c^2)(2ab-a^2-b^2+c^2)}} \\
&=& {\scriptsize \frac{1}{4} \sqrt{\{(a^2+2ab+b^2)-c^2\}\{-(a^2-2ab+b^2)+c^2\}}} \\
&=& \frac{1}{4} \sqrt{\{(a+b)^2-c^2\}\{c^2-(a-b)^2\}} \\
&\mathop{=}^{(4)}& {\scriptsize \frac{1}{4} \sqrt{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}} \\
&=& {\scriptsize \sqrt{\frac{(a+b+c)}{2}\frac{(a+b-c)}{2}\frac{(a-b+c)}{2}\frac{(-a+b+c)}{2}}} \\
&=& {\tiny \sqrt{\frac{(a+b+c)}{2}\{\frac{(a+b+c)}{2}-c\}\{\frac{(a+b+c)}{2}-b\}\{\frac{(a+b+c)}{2}-a\}}} \\
&\mathop{=}^{(5)}& \sqrt{s(s-c)(s-b)(s-a)} \\
&=& \sqrt{s(s-a)(s-b)(s-c)}
\end{eqnarray}$
(*)の部分までの変形を理解しておけば,ヘロンの公式を導かずとも,三角形の3辺の長さ $a,b,c$ の値から面積 $S$ を計算することができる.つまり,三角形の面積の公式と,三角比の関係式,および余弦定理を理解していれば,ヘロンの公式を暗記する必要はないともいえるが,試験での計算の効率化のためには,やはり公式を覚えておくのが望ましい.

